Giáo án powerpoint dạy thêm Toán 11 kết nối Bài 16: Giới hạn của hàm số

CHÀO MỪNG CÁC EM  

ĐẾN VỚI TIẾT HỌC HÔM NAY! 

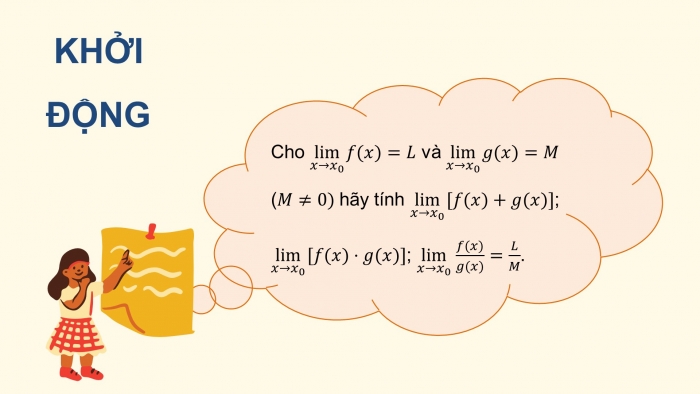
KHỞI ĐỘNG 

Cho lim┬(x→x_0 ) f(x)=L và lim┬(x→x_0 ) g(x)=M (M≠0) hãy tính lim┬(x→x_0 ) [f(x)+g(x)]; lim┬(x→x_0 ) [f(x)⋅g(x)]; lim┬(x→x_0 ) (f(x))/(g(x))=L/M. 

CHƯƠNG V: GIỚI HẠN.  

HÀM SỐ LIÊN TỤC 

BÀI 16: GIỚI HẠN  

CỦA HÀM SỐ 

HỆ THỐNG  

KIẾN THỨC 

1. Giới hạn hữu hạn của hàm số tại một điểm

Giả sử (a;b) là một khoảng chứa điểm x_0 và hàm số y=f(x) xác định trên khoảng (a;b), có thể trừ điểm x_0. Ta nói hàm số f(x) có giới hạn là số L khi x dần tới x_0 nếu với dãy số (x_n ) bất kì, x_n∈(a;b),x_n≠x_0 và x_n→x_0, ta có f(x_n )→L, kí hiệu lim_(x→x_0 ) f(x)=L hay f(x)→L khi x→x_0. 

• Quy tắc tính giới hạn

- Nếu lim┬(x→x_0 ) f(x)=L vàlim┬(x→x_0 ) g(x)=M thì 

lim┬(x→x_0 ) [f(x)+g(x)]=L+M;                     lim┬(x→x_0 ) [f(x)-g(x)]=L-M 

                 lim┬(x→x_0 ) [f(x)⋅g(x)]=L⋅M;                         lim┬(x→x_0 ) (f(x))/(g(x))=L/M," nếu " M≠0 

- Nếu f(x)≥0 với mọi x∈(a;b)∖{x_0 } và lim_(x→x_0 ) f(x)=L thì L≥0 và lim_(x→x_0 ) √(f(x))=√L. 

"Ví dụ:"  (lim)┬(x→2)  (x^2-x)/(x+1)=2/3 

• Giới hạn một bên

-Cho hàm số y=f(x) xác định trên khoảng (x_0;b). Ta nói số L là giới hạn bên phải của f(x) khi x→x_0 nếu với dãy số (x_n ) bất kì thoả mãn x_0<x_n<b và x_n→x_0, ta có f(x_n )→L, kí hiệu lim┬(x→x_0^+ ) f(x)=L. 

-Cho hàm số y=f(x) xác định trên khoảng (a;x_0 ). Ta nói số L là giới hạn bên trải của f(x) khi x→x_0 nếu với dãy số (x_n ) bất kì thoả mãn a <x_n<x_0 và x_n→x_0, ta có f(x_n )→L, kí hiệu lim┬(x→x_0^- ) f(x)=L. 

2. Giới hạn hữu hạn của hàm số tại vô cực

-Cho hàm số y=f(x) xác định trên khoảng (a;+∞). Ta nói hàm số f(x) có giới hạn là số L khi x→+∞ nếu với dãy số (x_n ) bất kì, x_n> a và x_n→+∞, ta có f(x_n )→L, kí hiệulim┬(x→+∞) f(x)=L hay f(x)→L khi x→+∞. 

-Cho hàm số y=f(x) xác định trên khoảng (-∞;b). Ta nói hàm số f(x) có giới hạn là số L khi x→-∞ nếu với dãy số (x_n ) bất kì, x_n<b và x_n→-∞, ta có f(x_n )→L, kí hiệulim┬(x→-∞) f(x)=L hay f(x)→L khi x→-∞. 

-Các quy tắc tính giới hạn hữu hạn tại một điểm cũng đúng cho giới hạn hữu hạn tại vô cực. 

-Với c là hằng số, ta có: lim┬(x→+∞) c=c,lim┬(x→-∞) c=c. 

-Với k là một số nguyên dương, ta có: 

lim┬(x→+∞) 1/x^k =0;  lim┬(x→-∞) 1/x^k =0 

3. Giới hạn vô cực của hàm số tại một điểm
4. a) Giới hạn vô cực

-Giả sử khoảng (a;b) chứa x_0 và hàm số y=f(x) xác định trên (a;b)∖{x_0 }. Ta nói hàm số f(x) có giới hạn +∞ khi x→x_0 nếu với dãy số (x_n ) bất kì, x_n∈(a;b)∖{x_0 },x_n→x_0, ta có f(x_n )→+∞, ki hiệu lim┬(x→x_o ) f(x)=+∞. 

-Ta nói hàm số f(x) có giới hạn -∞ khi x→x_0, kí hiệu lim┬(x→x_o ) f(x)=-∞, nếu lim┬(x→x_o ) [-f(x)]=+∞. 

-Cho hàm số y=f(x) xác định trên khoàng (x_0;b). Ta nói hàm số f(x) có giới hạn +∞ khi x→x_0 về bên phải nếu với dãy số (x_n ) bất kì thoả mãn x_0<x_n<b,x_n→x_0, ta có f(x_n )→+∞, ki hiệu lim┬(x→x_0^+ )⁡〖f(x)〗 =+∞. 

-Cho hàm số y=f(x) xác định trên khoảng (a;x_0 ). Ta nói hàm số f(x) có giới hạn +∞ khi x→x_0 về bên trải nếu với dãy số (x_n ) bất kì thoả mãn a<x_n<x_0,x_n→x_0, ta có f(x_n )→+∞, ki hiệu lim┬(x→x_0^- ) f(x)=+∞. 

-Các giới hạn một bên lim┬(x→x_0^+ ) f(x)=-∞ và lim┬(x→x_0^- ) f(x)=-∞ được định nghĩa tương tự. 

1. b) Một số quy tắc tính giới hạn vô cực

• Quy tắc tìm giới hạn của tích f(x)g(x).

Giả sử lim┬(x→x_o ) f(x)=L≠0 vàlim┬(x→x_o ) g(x)=+∞ (hoặc -∞ ).  

Khi đólim┬(x→x_o ) f(x)g(x) tính theo quy tắc 

• Quy tắc tìm giới hạn của thương

(f(x))/(g(x)) 

Các quy tắc trên vẫn đúng cho trường hợp: x→x_o^+;x→x_o^-. 

LUYỆN TẬP 

PHIẾU BÀI TẬP SỐ 1 

DẠNG 1: Sử dụng định nghĩa giới hạn dãy số và những quy tắc cơ bản 

Phương pháp giải:  

-Theo định nghĩa thì giới hạn hàm số f(x) trên cơ sở giới hạn các dãy f(x_n ). Nếu có 2 dãy x_n và x_n^′ cùng tiến đến x_0 mà lim⁡f (x_n )≠〖lim⁡f〗^′ (x_n^′ ) thì không tồn tại (lim)┬(x→x_0 ) f(x). 

-Với mọi số nguyên dương k, ta có: 

(lim)┬(x→+∞) x^k=+∞;(lim)┬(x→-∞) x^2k=+∞,(lim)┬(x→-∞) x^(2k+1)=-∞,(lim)┬(x→±∞)  1/x^k =0 

-Xác định dấu +∞ hoặc -∞ dựa trên dấu của tích số, thương số, x→x_0^+, x→x_0^-,x→±∞ 

Chú ý: Nếu hàm số f(x) là một đa thức, là một phân thức đại số hoặc một hàm số lượng giác có tập xác định là D thì với mỗi x_0∈D ta có (lim)┬(x→x_0 ) f(x)=f(x_0 ). 

Bài 1. Tính giới hạn của các hàm số:  a) f(x)=√(2x+10) khi x→-3  

Giải: 

Tập xác định của hàm số là ├ [-5;+∞┤) 

Chọn dãy số (x_n ) với x_n∈├ [-5;+∞┤) sao cho lim⁡〖x_n 〗=-3 

Theo định nghĩa (lim)┬(x→-3) √(2x+10)=(lim)┬(n→∞) √(2x_n+10) 

Theo định lí về giới hạn của dãy số, ta có  

(lim)┬(n→∞) √(2x_n+10)=√((lim)┬(n→∞) (2x_n+10) )=√(2.(lim)┬(n→∞) x_n+10)=√(2.(-3)+10) 

=√4=2.  

 Vậy (lim)┬(x→-3) √(2x+10)=2 

Tập xác định của hàm số là R nên chọn dãy số (x_n ) sao cho (lim)┬(n→∞) x_n=3 

Ta có  

(lim)┬(x→3)  f(x)=(lim)┬(x→3)   (2x+3)/(x^2+6)=(lim)┬(n→∞)  (2x_n+3)/(〖x_n〗^2+6)=((lim)┬(n→∞) (2x_n+3))/((lim)┬(n→∞) (〖x_n〗^2+6) ) 

                                         =(2.(lim)┬(n→∞) x_n+3)/((lim)┬(n→∞) x_n^2+6)=(2.3+3)/(3^2+6)=3/5 

"Vậy"  (lim)┬(x→3)  (2x+3)/(x^2+6)=3/5. 

"Bài 2. Tìm các giới hạn sau:" 

...