Giáo án điện tử chuyên đề Khoa học máy tính 11 kết nối Bài 1: Đệ quy và hàm đệ quy

CHÀO MỪNG CÁC EM ĐẾN VỚI BÀI HỌC MỚI!

KHỞI ĐỘNG

Hình 1.1. Búp bê Matryoshka

Hình 1.2. Lá dương xỉ

Hình 1.3. Cây súp lơ

Trong cuộc sống hằng ngày, các em thường gặp các hiện tượng sự vật, sự việc thể hiện sự giống hệt nhau, được lặp đi lặp lại với quy mô khác nhau. Ví dụ, búp bê Matryoshka rất nổi tiếng của Nga, khi mở búp bê mẹ ra chúng ta lại thấy búp bê con bên trong. Lá dương xỉ có mỗi nhánh lá có cấu trúc tổng thể của lá. Cây súp lơ có mỗi nhánh của cây súp lơ là hình ảnh thu nhỏ của cả cây súp lơ,…Em có thể nói gì về đặc điểm chung nhất của các búp bê Matryoshka, lá dương xỉ và cây súp lơ?

KHỞI ĐỘNG

Hình 1.1. Búp bê Matryoshka

Hình 1.2. Lá dương xỉ

Hình 1.3. Cây súp lơ

Có tính chất lặp lại của chính nó

CHUYÊN ĐỀ 1: THỰC HÀNH THIẾT KẾ THUẬT TOÁN THEO KĨ THUẬT ĐỆ QUY

BÀI 1.

ĐỆ QUY VÀ HÀM ĐỆ QUY

NỘI DUNG BÀI HỌC

Khái niệm đệ quy

1

Công thức truy hồi

2

Hàm đệ quy

3

KHÁI NIỆM ĐỆ QUY

1

Thảo luận nhóm và hoàn thành Hoạt động 1 SGK tr.5:

Hoạt động 1

Làm quen với đệ quy

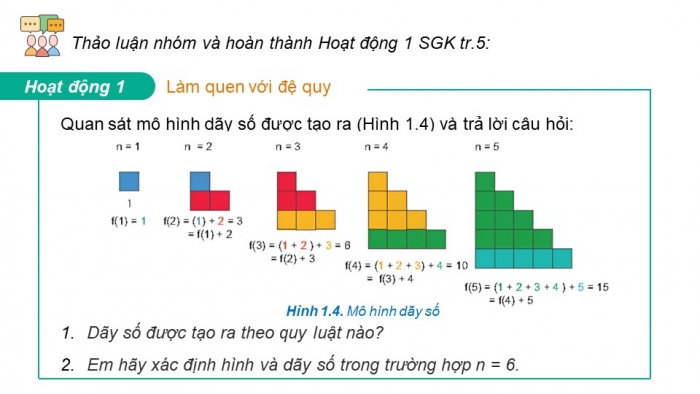
Quan sát mô hình dãy số được tạo ra (Hình 1.4) và trả lời câu hỏi:

• Dãy số được tạo ra theo quy luật nào?
• Em hãy xác định hình và dãy số trong trường hợp n = 6.

Hình 1.4. Mô hình dãy số

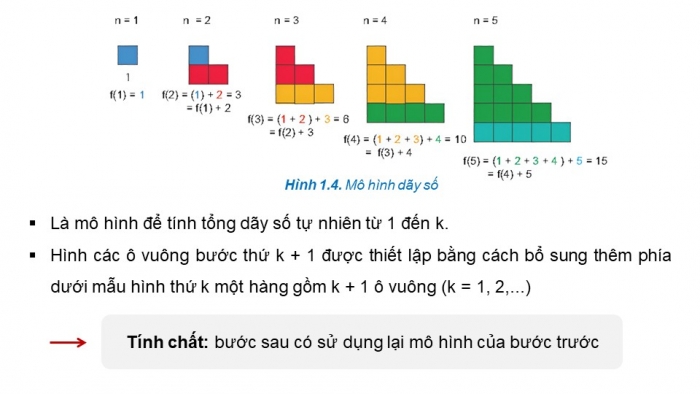
Hình 1.4. Mô hình dãy số

• Là mô hình để tính tổng dãy số tự nhiên từ 1 đến k.
• Hình các ô vuông bước thứ k + 1 được thiết lập bằng cách bổ sung thêm phía dưới mẫu hình thứ k một hàng gồm k + 1 ô vuông (k = 1, 2,...)

Tính chất: bước sau có sử dụng lại mô hình của bước trước

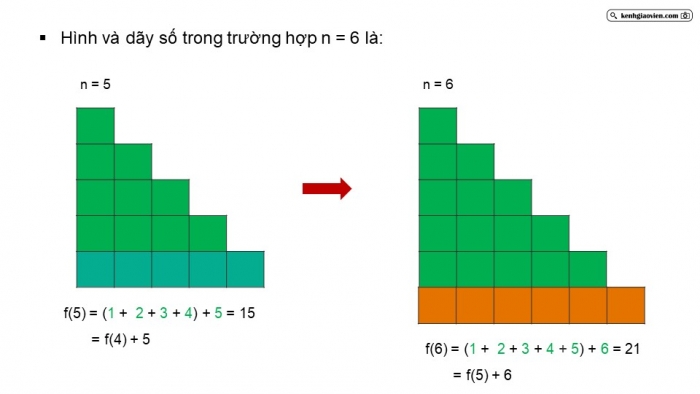
n = 5

f(5) = (1 + 2 + 3 + 4) + 5 = 15

= f(4) + 5

n = 6

f(6) = (1 + 2 + 3 + 4 + 5) + 6 = 21

= f(5) + 6

• Hình và dãy số trong trường hợp n = 6 là:

Khái niệm: Khi một sự vật, hiện tượng có tính chất lặp lại chính nó hoặc được định nghĩa theo chính sự vật, hiện tượng đó thì được gọi là đệ quy.

Ví dụ:

Dãy Fibonacci F(n) được định nghĩa đơn giản:

• F0 = 0; F1 = 1
• Fn = Fn – 1 + Fn – 2 với n >1

Thảo luận cặp đôi và trả lời câu hỏi:

A. Tổ ong

B. Bắp cải

C. Lát cắt hành

D. Ngôi sao

Câu 1: Trường hợp nào sau đây không có tính chất đệ quy?

Câu 2: Phát biểu nào sau đây sai về đệ quy?

A. Một đối tượng được gọi là đệ quy nếu nó hoặc một phần của nó được định nghĩa thông qua khái niệm về chính nó.

B. Đối tượng đệ quy thì sự vật, hiện tượng liên quan đến đối tượng sẽ được lặp lại nhiều lần.

C. Trong đệ quy, lời giải của một bài toán phụ thuộc vào lời giải của các trường hợp nhỏ hơn cả cùng một bài toán.

D. Đệ quy là cách gọi khác của lặp.

D. Đệ quy là cách gọi khác của lặp.

CÔNG THỨC TRUY HỒI

2

LÀM VIỆC NHÓM

Nhiệm vụ: Tìm hiểu một dãy số nổi tiếng để phát hiện các đặc điểm tương tự giữa các công thức này và khái niệm đệ quy.

Nhóm 1

Tìm hiểu dãy số Fibonacci

Nhóm 2

Tìm hiểu dãy số Lucas

Nhóm 3

Tìm hiểu dãy số Pell

a. Dãy số Fibonacci

• Là dãy số được phát hiện từ rất lâu và hiện nay phổ biến ở khắp các lĩnh vực khác nhau của khoa học.
• Dãy được định nghĩa như sau:
• F0 = 0, F1 = 1
• Fn = Fn – 1 + Fn – 2 với n > 1
• Đẳng thức a) được gọi là điều kiện ban đầu, hay cơ sở của dãy.
• Công thức b) được gọi là công thức truy hồi hay công thức đệ quy của dãy.

b. Dãy số Lucas

• Định nghĩa của dãy số giống với dãy số Fibonacci.
• L0 = 2, L1 = 1
• Ln = Ln – 1 + Ln – 2 với n > 1
• Công thức truy hồi của dãy số Lucas hoàn toàn giống với dãy Fibonacci.
• Phần tử ban đầu của dãy khác với dãy Fibonacci.

c. Dãy số Pell

• Dãy số Pell được định nghĩa như sau:
• P0 = 0, P1 = 1
• Pn = 2Pn – 1 + Pn – 2 với n > 1

• Tất cả các công thức truy hồi đều có hai phần:

KẾT LUẬN

Phần cơ sở

xác định các giá trị ban đầu

Phần truy hồi

để tính các phần tử tiếp theo

• Tất cả các dãy số được định nghĩa thông qua công thức truy hồi chính là được định nghĩa bằng khái niệm đệ quy.

Giữ nguyên nhóm, tiếp tục thảo luận để hoàn thành các bài tập trong phần Câu hỏi:

(1)

(2)

• Phần cơ sở: 0! = 1, 1! = 1.
• Phần đệ quy: n! = n × (n - 1)!



• Phần cơ sở: x0 = 1
• Phần đệ quy: xn = x × xn - 1



HÀM ĐỆ QUY

3

Hoạt động 3

Tìm hiểu và thiết lập hàm đệ quy

Bạn An được yêu cầu viết các hàm đệ quy cho các bài toán sau:

• Viết một hàm có chức năng in ra các số đếm ngược từ n xuống 1.
• Viết hàm tính số Fibonacci thứ n.

Chương trình 1.

• def countdown(n):
• print(n)
• countdown(n – 1)

Chương trình 2.

• def Fibonacci(n):
• return Fibonacci(n - 1) + Fibonacci(n – 2)

Các hàm trên của bạn An có đúng không?

• Cả hai chương trình của bạn An viết đều lỗi:

Chương trình 1

--------------- Còn tiếp ---------------