Giáo án điện tử chuyên đề Toán 11 cánh diều Bài 1: Một vài yếu tố của Lí thuyết đồ thị. Đường đi Euler và đường đi Hamilton
Tải giáo án điện tử Chuyên đề học tập Toán 11 cánh diều Bài 1: Một vài yếu tố của Lí thuyết đồ thị. Đường đi Euler và đường đi Hamilton. Bộ giáo án chuyên đề được thiết kế sinh động, đẹp mắt. Thao tác tải về đơn giản, dễ dàng sử dụng và chỉnh sửa. Thầy, cô kéo xuống để xem chi tiết.
Xem: => Giáo án toán 11 cánh diều
Xem toàn bộ: Giáo án điện tử chuyên đề toán 11 cánh diều
VUI MỪNG CHÀO ĐÓN CÁC EM QUAY TRỞ LẠI VỚI MÔN HỌC!
KHỞI ĐỘNG
Bài toán Bảy cây cầu của Euler (hay Bảy cây cầu ở Königsberg)
Thành phố Königsberg nằm trên sông Pregel, bao gồm hai hòn đảo lớn nối với nhau và nối với đất liền bởi bảy cây cầu.
Người dân có thắc mắc: “Có đường đi nào cho phép một người đi qua cả bảy cây cầu, mà mỗi cây cầu chỉ đi qua một lần?”.
Năm 1741, Euler đã trình bày lời giải cho Bài toán Bảy cây cầu ở Königsberg và đưa ra lời giải tổng quát cho dạng bài toán này, bất kể số lượng vùng đất cũng như số lượng cây cầu.
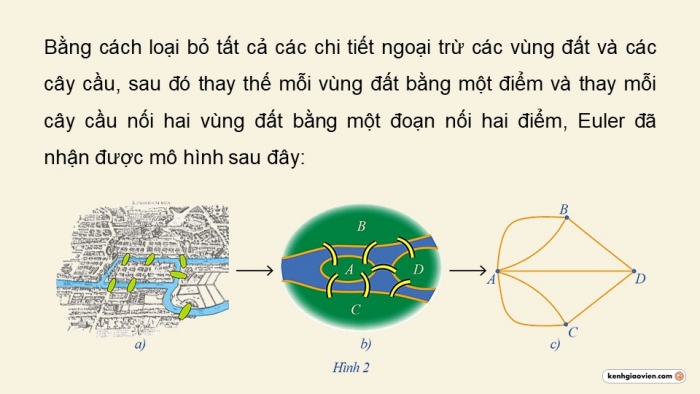
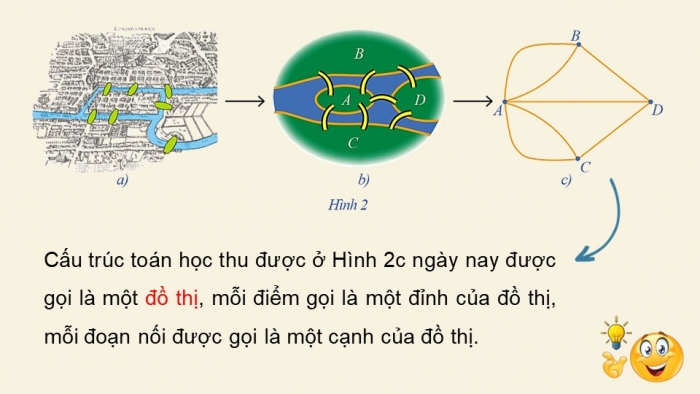
Bằng cách loại bỏ tất cả các chi tiết ngoại trừ các vùng đất và các cây cầu, sau đó thay thế mỗi vùng đất bằng một điểm và thay mỗi cây cầu nối hai vùng đất bằng một đoạn nối hai điểm, Euler đã nhận được mô hình sau đây:
CHUYÊN ĐỀ II: LÀM QUEN VỚI MỘT VÀI YẾU TỐ CỦA LÍ THUYẾT ĐỒ THỊ
BÀI 1: MỘT VÀI YẾU TỐ CỦA LÍ THUYẾT ĐỒ THỊ. ĐƯỜNG ĐI EULER VÀ ĐƯỜNG ĐI HAMILTON
NỘI DUNG BÀI HỌC
...........................................
KẾT LUẬN
Đồ thị 
được gọi là đồ thị đơn nếu mỗi cặp đỉnh của đồ thị chỉ có không quá một cạnh nối chúng và không có đỉnh nào được nối với chính nó bởi một cạnh của đồ thị.
Ví dụ 2:
Trong các đồ thị ở Hình 5, đồ thị nào là đồ thị đơn?
Nếu hai đầu mút của cạnh trùng nhau tại đỉnh 
thì ta gọi cạnh ấy là một khuyên, kí hiệu 
(Hình 5c).
Luyện tập 2:
Cho hai ví dụ về đồ thị đơn.
Ví dụ
Quy ước: Nếu không nói gì thêm, từ nay về sau các đồ thị đều được giả thiết là đồ thị đơn.
2. Bậc của đỉnh
HĐ3:
Quan sát đồ thị ở Hình 6 và đếm số cạnh của đồ thị nhận đỉnh 
làm đầu mút.
Nhận xét:
Có 3 cạnh của đồ thị nhận đỉnh 
làm đầu mút. Ta nói bậc của đỉnh 
bằng 3, kí hiệu là 
.
KẾT LUẬN
Bậc của một đỉnh 
trong đồ thị 
là số cạnh của đô thị nhận đỉnh 
làm đầu mút, kí hiệu là 
.
Chú ý: Một đỉnh của đồ thị có bậc 
nếu đỉnh đó là đầu mút của 
cạnh.
Ví dụ 3:
Trong đồ thị ở Hình 6, hãy tìm những đỉnh có:
a) Bậc lẻ; b) Bậc chẵn.
Giải
Do 
, 
, 
, 
, 
nên:
a) 
là các đỉnh bậc lẻ;
b) 
là các đỉnh bậc chẵn.
Luyện tập 3:
Có bao nhiêu đỉnh bậc lẻ trong đồ thị ở Hình 5a?
Các đỉnh bậc lẻ của đồ thị là: 
(đều có bậc 3).
HĐ4:
Quan sát đồ thị ở Hình 7 và cho biết:
- Tổng các bậc của năm đỉnh trong đồ thị đó;
- Số cạnh của đồ thị đó;
- Tổng các bậc của năm đỉnh trong đồ thị gấp bao nhiêu lần số cạnh của đồ thị đó.
ĐỊNH LÍ
Trong một đồ thị, tổng tất cả các bậc của các đỉnh bằng hai lần số cạnh của đồ thị đó.
Ví dụ 4:
Chứng minh rằng trong một đồ thị, số đỉnh có bậc lẻ là một số chẵn.
Giải
Theo định lí trên, tổng tất cả các bậc của các đỉnh bằng hai lần số cạnh của đồ thị đó, suy ra tổng tất cả các bậc của các đỉnh là số chẵn.
Vậy số đỉnh bậc lẻ là số chẵn.
Luyện tập 4:
Cho ví dụ về một đồ thị có số lẻ đỉnh bậc chẵn.
Ví dụ
Các đỉnh bậc chẵn là: 
.
3. Đường đi trên đồ thị
HĐ5:
Quan sát đồ thị ở Hình 7 và cho biết:
a) Hai đỉnh 
có được nối với nhau bằng một cạnh hay không;
b) Dãy các cạnh kế tiếp nhau 
có đặc điểm gì.
Giải
a) Hai đỉnh 
có được nối với nhau bằng một cạnh.
b) Dãy các cạnh kế tiếp nhau 
có đặc điểm: không có cạnh nòa xuất hiện hai lần, đỉnh cuối của cạnh bất kì là đỉnh đầu của cạnh tiếp theo, không có đỉnh nào được đi qua hai lần.
NHẬN XÉT
Hai đỉnh 
được nối với nhau bằng một cạnh của đồ thị. Ta nói hai đỉnh 
là kề nhau hay là láng giềng của nhau.
--------------- Còn tiếp ---------------
Trên chỉ là 1 phần của giáo án. Giáo án khi tải về có đầy đủ nội dung của bài. Đủ nội dung của học kì I + học kì II
Hệ thống có đủ tài liệu:
- Giáo án điện tử chuyên đề toán 11 cánh diều (350k)
- Giáo án toán 11 cánh diều (300k)
- Giáo án chuyên đề toán 11 cánh diều (300k)
- Giáo án powerpoint toán 11 cánh diều (350k)
- Giáo án dạy thêm toán 11 cánh diều (300k)
- Câu hỏi và bài tập trắc nghiệm toán 11 cánh diều (150k)
- Đề thi toán 11 cánh diều (150k)
- File bài tập toán 11 Cánh diều (150k)
- File word đáp án toán 11 cánh diều (100k)
- Bài tập file word Toán 11 Cánh diều (150k)
- Kiến thức trọng tâm Toán 11 cánh diều (150k)
- Đề kiểm tra 15 phút Toán 11 cánh diều (100k)
- Giáo án powerpoint chuyên đề toán 11 cánh diều (350k)
- Phiếu học tập theo bài Toán 11 cánh diều cả năm (150k)
- Trắc nghiệm đúng sai Toán 11 cánh diều cả năm (150k)
- Trắc nghiệm dạng câu trả lời ngắn Toán 11 cánh diều cả năm (150k)
=> Có thể chọn nâng cấp VIP với phí là 1050k để tải tất cả tài liệu ở trên
- Chỉ gửi 500k. Tải về dùng thực tế, 1 ngày sau mới gửi số còn lại.
Cách tải hoặc nâng cấp:
- Bước 1: Chuyển phí vào STK: 1214136868686 - cty Fidutech - MB
- Bước 2: Nhắn tin tới Zalo Fidutech - nhấn vào đây để thông báo và nhận tài liệu
Xem toàn bộ: Giáo án điện tử chuyên đề toán 11 cánh diều
ĐẦY ĐỦ GIÁO ÁN CÁC BỘ SÁCH KHÁC
GIÁO ÁN WORD LỚP 11 CÁNH DIỀU
GIÁO ÁN POWERPOINT LỚP 11 CÁNH DIỀU
GIÁO ÁN CHUYÊN ĐỀ LỚP 11 CÁNH DIỀU
Giáo án chuyên đề Công nghệ cơ khí 11 cánh diều đủ cả năm
Giáo án chuyên đề Tin học 11 Khoa học máy tính cánh diều đủ cả năm
Giáo án chuyên đề Tin học 11 Tin học ứng dụng cánh diều đủ cả năm
Giáo án chuyên đề Âm nhạc 11 cánh diều đủ cả năm
Giáo án chuyên đề Kinh tế pháp luật 11 cánh diều đủ cả năm
GIÁO ÁN DẠY THÊM LỚP 11 CÁNH DIỀU
Giáo án dạy thêm toán 11 cánh diều đủ cả năm
Giáo án dạy thêm ngữ văn 11 cánh diều đủ cả năm
CÁCH ĐẶT MUA:
Liên hệ Zalo: Fidutech - nhấn vào đây