Giáo án điện tử chuyên đề Khoa học máy tính 12 kết nối Bài 7: Cây tìm kiếm nhị phân

Tin học

CHÀO MỪNG CÁC EM

ĐẾN VỚI BÀI HỌC!

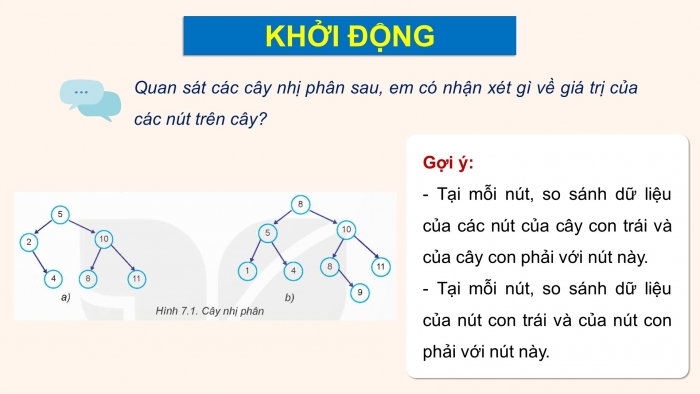
KHỞI ĐỘNG

Gợi ý:

- Tại mỗi nút, so sánh dữ liệu của các nút của cây con trái và của cây con phải với nút này.

- Tại mỗi nút, so sánh dữ liệu của nút con trái và của nút con phải với nút này.

Quan sát các cây nhị phân sau, em có nhận xét gì về giá trị của các nút trên cây?

Bài 7:

Cây tìm kiếm nhị phân

Cây tìm kiếm nhị phân

1

Chèn một khoá vào cây tìm kiếm nhị phân

2

Thuật toán tìm kiếm trên

cây tìm kiếm nhị phân

3

NỘI DUNG BÀI HỌC

PHẦN 1.

CÂY TÌM KIẾM NHỊ PHÂN

• Nêu khái niệm cây tìm kiếm nhị phân.
• Có thể biểu diễn dữ liệu cây nhị phân theo những cách nào? Trình bày cách biểu diễn.

Thảo luận, tìm hiểu nội dung mục 1

Cây tìm kiếm nhị phân (BST – Binary Search Tree) là một dạng đặc biệt của cây nhị phân thông thường, được tạo ra với mục đích hỗ trợ thuận tiện cho các bài toán tìm kiếm, chèn, xoá, sắp xếp.

Khái niệm

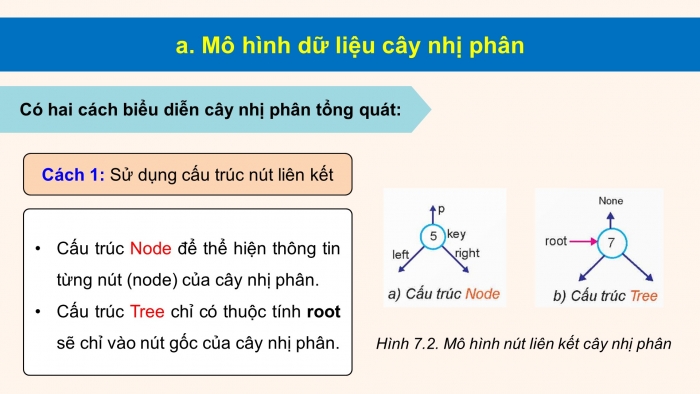
a. Mô hình dữ liệu cây nhị phân

Có hai cách biểu diễn cây nhị phân tổng quát:

Cách 1: Sử dụng cấu trúc nút liên kết

• Cấu trúc Node để thể hiện thông tin từng nút (node) của cây nhị phân.
• Cấu trúc Tree chỉ có thuộc tính root sẽ chỉ vào nút gốc của cây nhị phân.

Hình 7.2. Mô hình nút liên kết cây nhị phân

a. Mô hình dữ liệu cây nhị phân

Có hai cách biểu diễn cây nhị phân tổng quát:

Cách 2: Sử dụng mảng một chiều

Cây nhị phân tổng quát cần được bổ sung thêm các nút giả (có giá trị None) để tạo thành cây nhị phân hoàn chỉnh đã biến đổi.

Sử dụng cách biểu diễn cây hoàn chỉnh này để biểu diễn.

a. Mô hình dữ liệu cây nhị phân

Ví dụ: Cho mảng T = [5, 3, 7, 6]

Cây nhị phân tổng quát ở Hình 7.3c được thêm vào các nút giả None để trở thành cây nhị phân hoàn chỉnh và được cài đặt bằng mảng T = [5, 3, 7, None, None, 6].

a. Mô hình dữ liệu cây nhị phân

Để thiết lập nhị phân rỗng, sử dụng hàm:

b. Cây tìm kiếm nhị phân

Thế nào là cây tìm kiếm nhị phân?

Khái niệm

Cây tìm kiếm nhị phân là cây nhị phân, có hai tính chất quan trọng:

• Khoá của mỗi nút của cây lớn hơn khoá của tất cả các nút thuộc cây con trái và nhỏ hơn khoá của tất cả các nút thuộc cây con phải của nó.
• Hai nút khác nhau có khoá khác nhau.

Cây tìm kiếm nhị phân

Cây tìm kiếm nhị phân mà tại mọi nút thì chiều cao của cây con trái và của cây con phải lệch nhau nhiều nhất là 1.

Cây tìm kiếm nhị phân có chiều cao lớn nhất, mỗi nút chỉ có tối đa một nút con.

Thuật toán tìm kiếm nhị phân

Thuật toán tìm kiếm tuần tự

Cây cân bằng

Cây suy biến

b. Cây tìm kiếm nhị phân

Khi cây tìm kiếm nhị phân được cài đặt bằng mảng T, tại mọi nút k, với mọi nút i thuộc cây con trái và với mọi nút j thuộc cây con phải, ta có bất đẳng thức:

T[i] < T[k] < T[j]

Lưu ý: Nếu cây nhị phân T là cây tìm kiếm nhị phân thì mọi cây con của T cũng là cây tìm kiếm nhị phân

CỦNG CỐ

1

Trong Hình 7.5, em hãy cho biết cây nào là cây tìm kiếm nhị phân.

2

Từ các khóa 1, 2, 3 có thể tạo ra được bao nhiêu cây tìm kiếm nhị phân? Hãy vẽ sơ đồ mô tả các cây này.

Có 5 cách thiết lập cây tìm kiếm nhị phân từ các khóa 1, 2, 3.

KẾT LUẬN

• Cây nhị phân tổng quát có thể được cài đặt bằng cấu trúc nút liên kết hoặc bằng mảng một chiều.
• Cây tìm kiếm nhị phân là cây nhị phân mà tại mọi nút, khoá của nút này lớn hơn khoá của các nút con thuộc cây con trái và nhỏ hơn khoá của các nút con thuộc cây con phải.
• Khoá của các nút là duy nhất, nghĩa là hai nút khác nhau có khoá khác nhau.

PHẦN 2.

CHÈN MỘT KHOÁ VÀO CÂY TÌM KIẾM NHỊ PHÂN

Cho cây tìm kiếm nhị phân T. Yêu cầu chèn khoá v vào cây T sao cho sau khi chèn khoá v thì cây T vẫn là cây tìm kiếm nhị phân. Quan sát, thảo luận, tìm hiểu thuật toán tìm kiếm khoá 7 trên cây tìm kiếm nhị phân và cách chèn khoá 7 vào cây này.

BÀI TOÁN

Nêu các bước chính để chèn một khóa v vào cây tìm kiếm nhị phân T.

Thiết lập cấu trúc nút mới với khoá 7 sẵn sàng chèn vào cây tìm kiếm nhị phân T.

Bước 1: Tìm vị trí cần chèn khoá v trên cây T

Bắt đầu từ nút gốc.

Vì nút gốc có khoá 5 < 7, nên sẽ chuyển tìm tiếp sang nút con phải của nút gốc (với khoá 10).

Nút hiện thời có khoá 10 > 7 nên sẽ chuyển tìm tiếp sang nút con trái của nút hiện thời (với khoá 8).

Nút hiện thời là 8 > 7 nên sẽ chuyển tìm tiếp sang nút con trái của nút hiện thời. Nhưng nút con trái này là None, do vậy đây chính là vị trí cần chèn nút mới.

Bước 2: Chèn khoá v vào cây T

Chèn nút mới với khoá 7 vào vị trí là nút con trái của nút với khoá 8.

Trong trường hợp khoá v không có trong cây T thì chèn khoá v vào cây này bằng cách tạo nút thật mới tại nút giả None và gán khoá v cho nút mới này.

Bước 1. Tìm vị trí chính xác cần chèn. Nếu gặp khoá v thì dứng chương trình.

Bước 2. Thực hiện thao tác chèn.

KẾT LUẬN

Quá trình chèn một khoá v vào cây tìm kiếm nhị phân T gồm hai bước:

Đoạn chương trình mô tả thao tác chèn một khóa vào cây tìm kiếm nhị phân

1

Thực hiện tim vị trí cần chèn khoá v bắt đầu từ nút gốc T[0] cho đến khi gặp nút giả T[k] = None hoặc tìm thấy nút T[k] = v thì kết thúc.

2

Thực hiện chèn khoá v vào cây T tại nút k. Nếu k len(T) thì ta phải thêm các nút giá None từ chỉ số len(T) đến chỉ số k để cây T là cây nhị phân hoàn chỉnh. Số nút giả None phải thêm vào là k - len(T) + 1.

Đoạn chương trình

Hàm Tree_Insert(T, v) dùng để chèn khoá v vào cây tìm kiếm nhị phân T được cài đặt bằng một danh sách (thuộc kiểu list của Python).

Đoạn chương trình

Đoạn chương trình sau thực hiện việc tạo cây tìm kiếm nhị phân từ một tập hợp các phần tử cho trước.

Câu 1. Cho trước dây các số A = [10,1,2,11,8,15,20,9,0]. Hãy mô tả và vẽ sơ đồ cây nhị phân biểu diễn dãy số trên sau khi thực hiện thao tác chèn như đã mô tả trong hoạt động.

Câu 2. Với cây nhị phân đã có ở Câu 1, em hãy vẽ sơ đồ cây sau khi chèn khoá 14 và cho biết vị trí của khoá này ở trong cây.

CỦNG CỐ

Câu 1.

Kết quả cây tìm kiếm nhị phân

Câu 2.

Sơ đồ cây sau khi chèn khóa 14:

Chèn khoá 14 vào vị trí là nút con trái của nút với khoá 15

Quá trình chèn một khoá v vào cây tìm kiếm nhị phân T gồm hai bước:

KẾT LUẬN

• Bước 1. Tìm vị trí chính xác cần chèn. Nếu gặp khoá v thì dùng chương trình.
• Bước 2. Thực hiện thao tác chèn.

PHẦN 3.

THUẬT TOÁN TÌM KIẾM TRÊN CÂY TÌM KIẾM NHỊ PHÂN

HOẠT ĐỘNG 3

a) Tìm kiếm khoá 18. Trình tự tìm kiếm: 11 20 15 16 None (không tìm thấy).

b) Tìm kiếm khoá 7. Trình tự tìm kiếm: 11 4 7 (tìm thấy)

Thuật toán: Tìm kiếm một nút với khóa v

Bắt đầu từ nút có chỉ số k trên cây tìm kiếm nhị phân T. Nếu tìm thấy thì hàm trả về chỉ số của nút có giá trị v, ngược lại trả về -1.

Việc tìm kiếm được thực hiện như sau:

Nếu k nằm ngoài khoảng chỉ số của T hoặc T[k] = None thì trả về -1.

Nếu T[k] = v thì dừng tìm kiếm và trả về k.

Nếu T[k] v thì sẽ tìm tiếp trong cây con trái nếu v < T[k], ngược lại tìm tiếp trong cây con phải nếu T[k] < v.

Chương trình tìm kiếm một nút với khóa v

Cách 1: Sử dụng kĩ thuật đệ quy

Hàm tìm kiếm sử dụng đệ quy

Chương trình tìm kiếm một nút với khóa v

Cách 2: Không sử dụng kĩ thuật đệ quy

Hàm tìm kiếm không sử dụng đệ quy

Chương trình tìm kiếm một nút với khóa v

Cả hai cách này đều có độ phức tạp thời gian O(h) với h là chiều cao của cây tìm kiếm nhị phân.

Ví dụ:

Đoạn mã sau đây tìm khoá v trên cây tìm kiếm nhị phân T và trả về chỉ số k >= 0 nếu tìm thấy, sau đó hiển thị kết quả tìm kiếm.

Câu 1. Khi nào việc tìm kiếm trên cây tìm kiếm nhị phân là:

a) nhanh nhất? b) chậm nhất?

Câu 2. Cây tìm kiếm nhị phân T được thiết lập bằng cách chèn lần lượt các phần tử 3, 1, 6, 5, 0, 2, 4. Dùng sơ đồ mô tả các bước tìm kiếm giá trị khoá là:

a) 4.

b) 10.

c) 0.

a) Nhanh nhất khi giá trị tìm kiếm trùng với khoá của nút gốc.

b) Chậm nhất khi cây tìm kiếm nhị phân suy biến chỉ có một nhánh, giá trị tìm kiếm trùng với khoá tại nút cuối cùng của nhánh này.

Trả lời câu 1

Cây tìm kiếm nhị phân được xây dựng có dạng sau:

Các bước tìm kiếm sẽ là:

a) 3 → 6 → 5 → 4, tìm thấy.

b) 3 → 6 → None, không tìm thấy.

c) 3 → 1 → 0, tìm thấy

Trả lời câu 2

KẾT LUẬN

Thuật toán tìm kiếm khoá K trong cây tìm kiếm nhị phân có độ phức tạp thời gian 0(h), với h là chiều cao của cây, hay tương đương trong trường hợp trung bình là O(logn) với n là số nút của cây.

LUYỆN TẬP

Câu 1: Trong các câu sau, câu khẳng định nào sai.

A. Trong cây tìm kiếm nhị phân, giá trị khoá mọi nút của cây con trái và cây con phải đều nhỏ hơn giá trị khoá của nút gốc.

B. Cây tìm kiếm nhị phân suy biến tốn ít thời gian để tìm kiếm một khóa hơn so với cây cân bằng.

C. Để tìm kiếm một khóa trên cây tìm kiếm nhị phân cân bằng ta có thể sử dụng thuật toán tìm kiếm nhị phân.

D. Quá trình tìm kiếm trên cây tìm kiếm nhị phân luôn cho kết quả là tìm được nút có giá trị bằng giá trị khoá cho trước.

B. Cây tìm kiếm nhị phân suy biến tốn ít thời gian để tìm kiếm một khóa hơn so với cây cân bằng.

Câu 2: Cho n là số nút của cây tìm kiếm nhị phân. Thuật toán tìm khóa K trong cây tìm kiếm nhị phân có độ phức tạp thời gian là:

--------------- Còn tiếp ---------------