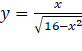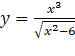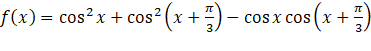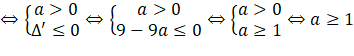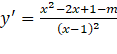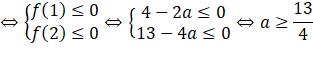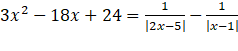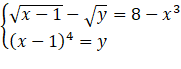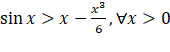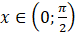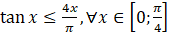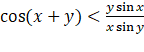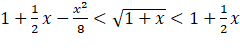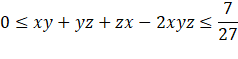Giáo án bồi dưỡng học sinh giỏi Toán 12
Giáo án Chuyên đề Bồi dưỡng học sinh giỏi môn Toán 12 dùng chung cho các bộ sách mới: Kết nối tri thức với cuộc sống, Chân trời sáng tạo, Cánh diều. Bộ tài liệu soạn theo chủ đề bao gồm tóm tắt lí thuyết, câu hỏi và bài tập sẽ giúp học sinh ôn luyện nâng cao, ôn thi HSG đạt kết quả tốt. Giáo án tải về và chỉnh sửa được. Mời thầy cô tham khảo.
Click vào ảnh dưới đây để xem giáo án rõ












Phần trình bày nội dung giáo án
CHUYÊN ĐỀ 1 – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
CHỦ ĐỀ 1: TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ
A. TÓM TẮT KIẾN THỨC LÝ THUYẾT
1. Khái niệm tính đơn điệu của hàm số
Giả sử ![]() là một khoảng, một đoạn hoặc một nửa khoảng và
là một khoảng, một đoạn hoặc một nửa khoảng và ![]() là hàm số xác định trên
là hàm số xác định trên ![]() .
.
Hàm số
 được gọi là đồng biến trên
được gọi là đồng biến trên  nếu
nếu 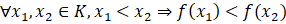 .
.Hàm số
 được gọi là nghịch biến trên
được gọi là nghịch biến trên  nếu
nếu  .
.
2. Mối quan hệ giữa tính đơn điệu và dấu của đạo hàm
Cho hàm số ![]() có đạo hàm trên khoảng
có đạo hàm trên khoảng ![]() .
.
a) Nếu ![]() với mọi
với mọi ![]() thì hàm số
thì hàm số ![]() đồng biến trên khoảng
đồng biến trên khoảng ![]() .
.
b) Nếu ![]() với mọi
với mọi ![]() thì hàm số
thì hàm số ![]() nghịch biến trên khoảng
nghịch biến trên khoảng ![]() .
.
Chú ý
+ Định lí vẫn đúng trong trường hợp ![]() tại một số hữu hạn điểm trong khoảng
tại một số hữu hạn điểm trong khoảng ![]() .
.
+ Nếu ![]() với mọi
với mọi ![]() thì hàm số
thì hàm số ![]() không đổi trên khoảng
không đổi trên khoảng ![]() .
.
3. Sử dụng bảng biến thiên xét tính đơn điệu của hàm số
Bước 1. Tìm tập xác định của hàm số.
Bước 2. Tính đạo hàm ![]() . Tìm các điểm
. Tìm các điểm ![]() mà tại đó đạo hàm bằng 0 hoặc không tồn tại.
mà tại đó đạo hàm bằng 0 hoặc không tồn tại.
Bước 3. Sắp xếp các điểm ![]() theo thứ tự tăng dẫn và lập bảng biến thiên của hàm số.
theo thứ tự tăng dẫn và lập bảng biến thiên của hàm số.
Bước 4. Nêu kết luận về khoảng đồng biến, nghịch biến của hàm số.
B. CÁC DẠNG BÀI TẬP
Dạng 1. Xét tính đồng biến, nghịch biến, hàm hằng. Phương pháp giải: - Tìm tập xác định. - Tính đạo hàm, xét dấu đạo hàm, lập bảng biến thiên. - Kết luận
Bài 1. Xét chiều biến thiên của hàm số: a) c) Gợi ý lời giải: a) Tập xác định: Cho Bảng biến thiên:
Vậy hàm số nghịch biến trên b) Tập xác định:
c) Tập xác định: Cho Bảng biến thiên:
Vậy hàm số đồng biến trên mỗi khoảng d) Tập xác định: Vì Bài 2. Xét chiều biến thiên của hàm số: a) Gợi ý lời giải: a) Tập xác định: Ta có: Bảng biến thiên:
Vậy hàm số đồng biến trên khoảng b) Tập xác định: Ta có: c) Tập xác định: Ta có: d) Tập xác định: Ta có:
Bài 3. Tìm các khoảng đơn điệu của hàm số: a) Gợi ý lời giải: a) Tập xác định:
Bảng biến thiên:
Vậy hàm số đồng biến trên khoảng b) Tập xác định: Do đó Bài 4. Xét sự biến thiên của hàm số: a) c) Gợi ý lời giải: a) Tập xác định: Với Bảng biến thiên:
Vậy hàm số đồng biến trên khoảng Do hàm số b) Tập xác định: Ta có:
c) Tập xác định: Ta có: Vậy hàm số đồng biến trên khoảng d) Tập xác định: Với Bảng biến thiên:
Vậy hàm số đồng biến trên Bài 5. Tìm khoảng đơn điệu của hàm số a) c) Gợi ý lời giải: a) Tập xác định:
Bảng biến thiên:
Vậy hàm số nghịch biến trên khoảng b) Tập xác định: Với
Vậy hàm số đồng biến trên các khoảng c) Tập xác định: Ta có: Bảng biến thiên:
Vậy hàm số đồng biến trên các khoảng d) Tập xác định: Ta có: Vậy hàm số đồng biến trên khoảng Bài 6. Xét sự biến thiên của hàm số: a) Gợi ý lời giải: a) Tập xác định: Ta có: b) Tập xác định: Ta có:
Hàm số liên tục trên mỗi đoạn Vậy hàm số đồng biến trên Bài 7. Tìm khoảng đồng biến, nghịch biến của hàm số: a) Gợi ý lời giải: a)
b)
Vậy hàm số đồng biến trên khoảng Bài 8. Chứng minh các hàm số sau nghịch biến trên a) Gợi ý lời giải: a) Ta có: Vì b)
Hàm số liên tục trên mỗi đoạn Vậy hàm số nghịch biến trên Bài 9. Chứng minh: a) Gợi ý lời giải: a) Xét Có Do đó b) Xét Có Suy ra hàm số Do đó Bài 10. Chứng minh các hàm số sau là hàm không đổi a) b) Gợi ý lời giải: a)
Do đó b) Đạo hàm theo biến
Do đó Bài 11. Tìm các giá trị của a) b) Gợi ý lời giải: a) - Nếu - Nếu - Nếu - Nếu Vậy hàm số đồng biến trên b) Xét Xét
Bài 12. Tìm các giá trị của a) b) Gợi ý lời giải: a) - Nếu - Nếu - Nếu Bảng biến thiên:
Do đó hàm số đồng biến trên khoảng Vậy hàm số nghịch biến trên b) Vì Bài 13. Tìm các giá trị của a) b) Gợi ý lời giải: a) Tập xác định:
Hàm số đồng biến trên mỗi khoảng xác định b) Ta có: - Nếu - Nếu
Bảng biến thiên:
Hàm số nghịch biến trên mỗi khoảng Vậy hàm số đồng biến trên mỗi khoảng xác định của nó khi và chỉ khi Bài 14. Tìm a) b) Gợi ý lời giải: a) Hàm số nghịch biến trên khoảng
b)
Vì Bài 15. Tìm Gợi ý lời giải: Tập xác định: Có Xét Xét Bảng biến thiên:
Theo đề bài:
(thỏa mãn) |
Dạng 2. Ứng dụng tính đơn điệu vào giải phương trình, bất phương trình,.. Phương pháp giải: - Xét Nếu hàm số Nếu
Bài 1. Giải phương trình: Gợi ý lời giải: Đặt Xét hàm số Với Ta có:
Bài 2. Giải phương trình: Gợi ý lời giải: Điều kiện xác định:
Phương trình tương đương: Xét hàm số Ta có: Vậy phương trình có nghiệm duy nhất Bài 3. Giải phương trình: Gợi ý lời giải: Điều kiện: Ta có: Chia 2 vế cho
Xét
Do đó hàm số Bài 4. Giải phương trình: Gợi ý lời giải: Điều kiện: Phương trình trở thành: Xét Ta có: Phương trình:
Vậy phương trình đã cho có nghiệm là Bài 5. Giải bất phương trình: Gợi ý lời giải: Bất phương trình trở thành:
Xét hàm số Ta có: Khi đó: Xét Xét Vậy tập nghiệm là Bài 6. Giải bất phương trình: Gợi ý lời giải: Điều kiện: Bất phương trình viết lại: Xét
Ta có: Vậy tập nghiệm của bất phương trình là Bài 7. Giải bất phương trình:
Gợi ý lời giải: Điều kiện:
Ta có: Mặt khác Bài 8. Giải hệ phương trình: Gợi ý lời giải: Xét hàm số
Ta có hệ phương trình: Giả sử Giả sử Giả sử
Thử lại Vậy hệ phương trình có 2 nghiệm Bài 9. Giải hệ phương trình: Gợi ý lời giải: Ta có: Tương tự Ta có hệ: Giả sử Do đó Tương tự Ta có: Vậy hệ có nghiệm duy nhất Bài 10. Giải hệ phương trình: Gợi ý lời giải: Ta có: Đặt Giả sử - Nếu Ta có phương trình: - Nếu Do đó
Ta có phương trình Xét Vậy hệ có 2 nghiệm Bài 11. Giải hệ phương trình: Gợi ý lời giải: Điều kiện:
Xét hàm số Ta có: Phương trình (1) có dạng Vậy nghiệm của phương trình là Bài 12. Giải hệ bất phương trình: Gợi ý lời giải: Ta có (1) Xét (2): Đặt
Do đó Vậy tập nghiệm của hệ bất phương trình là Bài 13. Chứng minh rằng phương trình Gợi ý lời giải: Hàm Vì Mặt khác, ta có Vậy phương trình đó chỉ có một nghiệm duy nhất. Bài 14. Tìm số nghiệm của phương trình:
Gợi ý lời giải: Phương trình tương đương:
Xét phương trình: Do đó Do đó nghiệm của phương trình Đặt
Do đó Vậy phương trình có đúng 2 nghiệm. |
Dạng 3. Ứng dụng tính đơn điệu vào chứng minh bất đẳng thức Phương pháp giải: Nếu Đối với Việc xét dấu Nếu Bài 1. Chứng minh các bất đẳng thức sau: a) b) Gợi ý lời giải: a) Với Với Với Với b) Với Do đó hàm số
Suy ra với mọi Bài 2. Chứng minh: Gợi ý lời giải: Bất đẳng thức trở thành: Xét
Bài 3. Chứng minh các bất đẳng thức với mọi a) c) Gợi ý lời giải: a) Hàm số b) Hàm số Do đó, hàm số f đồng biến trên nửa khoảng c) Hàm số Do đó hàm số f đồng biến trên Kết quả: Tam giác d) Hàm số Do đó hàm số f đồng biến trên Bài 4. Chứng minh các bất đẳng thức: a) b) Gợi ý lời giải: a) Xét hàm số
b) Nếu Nếu Xét
Vì Bài 5. Chứng minh các bất đẳng thức: a) b) Gợi ý lời giải: a) Xét
Xét b) Xét hàm số: Ta có: Nếu Nếu Nếu Do đó Từ giả thiết có Do
Bài 6. Chứng minh các bất đẳng thức sau: a) b) Gợi ý lời giải: a) Không mất tính tổng quát, giả sử Xem vế trái là hàm số
b) Xét hàm số
Xét hàm số Ta có: Bài 7. Cho
Gợi ý lời giải: Giả sử
Và ta có
Xét |

Đủ kho tài liệu môn học
=> Tài liệu sẽ được gửi ngay và luôn
Cách tải:
- Bước 1: Chuyển phí vào STK: 1214136868686 - cty Fidutech - MB
- Bước 2: Nhắn tin tới Zalo Fidutech - nhấn vào đây để thông báo và nhận tài liệu