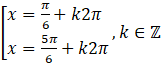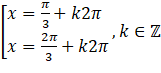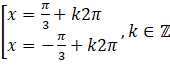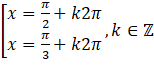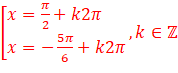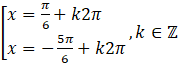Ôn thi tốt nghiệp THPT quốc gia môn Toán
Tài liệu ôn thi tốt nghiệp THPT quốc gia môn Toán. Theo đó, bộ tài liệu được áp dụng chung cho ba bộ sách hiện hành: Kết nối tri thức với cuộc sống, Chân trời sáng tạo và Cánh diều. Cấu trúc tài liệu gồm: Kiến thức cơ bản, các dạng câu hỏi trắc nghiệm (nhiều phương án lựa chọn, đúng/sai và câu hỏi trả lời ngắn). Đây là tài liệu hữu ích để học sinh có thể củng cố và ôn luyện. Mời thầy cô cùng tham khảo.
Phần trình bày nội dung giáo án
PHẦN I. HƯỚNG DẪN ÔN LUYỆN KIẾN THỨC
CHỦ ĐỀ 1: PHƯƠNG TRÌNH VÀ BẤT PHƯƠNG TRÌNH
A. KIẾN THỨC CƠ BẢN
I. PHƯƠNG TRÌNH LƯỢNG GIÁC
1. Phương trình lượng giác cơ bản
a) Phương trình 
- Với
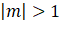, phương trình (1) vô nghiệm. - Với
, gọi 
là số thực thuộc đoạn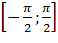 
sao cho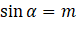 
Khi đó, ta có: 
.
Chú ý:
- Ta có một số trường hợp đặc biệt sau của phương trình 
:
;
.
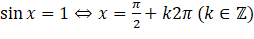- Nếu 
là góc lượng giác có đơn vị đo là độ thì ta có thể tìm góc lượng giác 
sao cho 
như sau:
b) Phương trình 
- Với
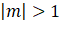, phương trình (2) vô nghiệm. - Với
, gọi 
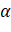là số thực thuộc đoạn 
sao cho 
Khi đó, ta có: 
.
Chú ý:
- Ta có một số trường hợp đặc biệt sau của phương trình 
:
;
.
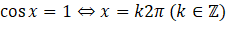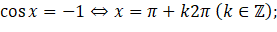
- Nếu 
là góc lượng giác có đơn vị đo là độ thì ta có thể tìm góc lượng giác 
sao cho 
như sau:
c) Phương trình 
Gọi 
là số thực thuộc khoảng 
sao cho 
. Khi đó, ta có:
Chú ý: Nếu 
là góc lượng giác có đơn vị đo là độ thì ta có thể tìm góc lượng giác 
sao cho 
như sau:
d) Phương trình 
Gọi 
là số thực thuộc khoảng 
sao cho 
. Khi đó, ta có:
Chú ý: Nếu 
là góc lượng giác có đơn vị đo là độ thì ta có thể tìm góc lượng giác 
sao cho 
như sau:
2. Phương trình lượng giác đưa về dạng cơ bản
.
.- Với phương trình có dạng:
ta có thể dùng công thức hạ bậc để đưa về phương trình dạng 
.
- Với một số phương trình lượng giác, ta có thể dùng các công thức lượng giác và các biến đổi để đưa về phương trình dạng tích
.
II. PHƯƠNG TRÌNH, BẤT PHƯƠNG TRÌNH MŨ VÀ LÔGARIT
1. Phương trình mũ
Với 
thì:
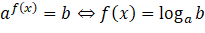với 
;
.
2. Phương trình lôgarit
Với 
thì:
.
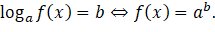
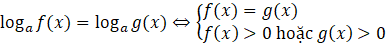3. Bất phương trình mũ
-------------------- Vẫn còn tiếp --------------------
B. CÂU HỎI ÔN TẬP
I. CÂU HỎI TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN
Câu 1. Nghiệm của phương trình 
là:
A. | B. |
C. | D. |
Câu 2. Phương trình nào sau đây có nghiệm?
A. | B. |
C. | D. |
Câu 3. Nghiệm của phương trình 
là:
A. | B. |
C. | D. |
Câu 4. Nghiệm của phương trình 
là:
A. | B. |
C. | D. |
Câu 5. Tập nghiệm của phương trình 
là:
A. | B. |
C. | D. |
Câu 6. Nghiệm của phương trình 
là:
A. | B. |
C. | D. |
Câu 7. Giải phương trình 
.
A. | B. |
C. | D. |
Câu 8. Giải phương trình 
:
A. | B. |
C. | D. |
Câu 9. Phương trình 
có nghiệm là:
A. | B. |
C. | D. |
Câu 10. Nghiệm của phương trình 
là:
A. | B. |
C. | D. |
Câu 11. Nghiệm của phương trình 
là:
A. 
.
B. 
.
C. 
.
D. 
.
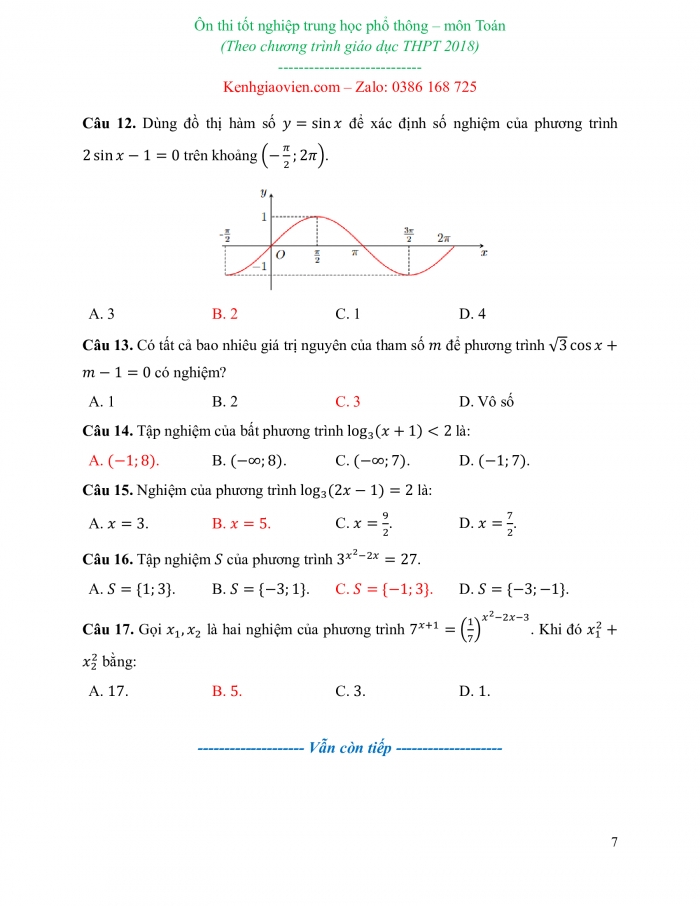
Câu 12. Dùng đồ thị hàm số 
để xác định số nghiệm của phương trình 
trên khoảng 
.
A. 3 | B. 2 | C. 1 | D. 4 |
Câu 13. Có tất cả bao nhiêu giá trị nguyên của tham số 
để phương trình 
có nghiệm?
A. 1 | B. 2 | C. 3 | D. Vô số |
Câu 14. Tập nghiệm của bất phương trình 
là:
A. | B. | C. | D. |
Câu 15. Nghiệm của phương trình 
là:
A. | B. | C. | D. |
Câu 16. Tập nghiệm 
của phương trình 
.
A. | B. | C. | D. |
Câu 17. Gọi 
là hai nghiệm của phương trình 
. Khi đó 
bằng:
A. | B. | C. | D. |
-------------------- Vẫn còn tiếp --------------------
II. CÂU HỎI TRẮC NGHIỆM ĐÚNG - SAI
Câu 1. Cho phương trình lượng giác 
(*). Khi đó:
a) Phương trình (*) tương đương 
.
b) Trong khoảng 
phương trình có 3 nghiệm.
c) Tổng các nghiệm của phương trình trong khoảng 
bằng 
.
d) Trong khoảng 
phương trình có nghiệm lớn nhất bằng 
.
Đáp án:
a – S b – S c – Đ d - Đ
Câu 2. Cho phương trình lượng giác 
(*). Khi đó:
a) Phương trình (*) có nghiệm 
.
b) Phương trình có nghiệm âm lớn nhất bằng 
.
c) Tổng các nghiệm của phương trình trong khoảng 
bằng 
.
d) Trong khoảng 
phương trình có nghiệm lớn nhất bằng 
.
Đáp án:
a – Đ b – S c – S d - S
Câu 3. Cho phương trình lượng giác 
.
a) Phương trình có nghiệm 
.
b) Phương trình có nghiệm âm lớn nhất bằng 
.
c) Khi 
thì phương trình có ba nghiệm.
d) Tổng các nghiệm của phương trình trong khoảng 
bằng 
Đáp án:
a – S b – S c – S d - Đ
Câu 4. Cho phương trình 
.
a) Phương trình có nghiệm 
.
b) Trong khoảng 
phương trình có 2 nghiệm.
c) Tổng các nghiệm của phương trình trong khoảng 
bằng 
.
d) Trong khoảng 
phương trình có nghiệm lớn nhất bằng 
.
Đáp án:
a – Đ b – Đ c – S d - Đ
Câu 5. Cho phương trình 
:
a) Phương trình tương đương 
.
b) Phương trình có nghiệm là: 
.
c) Phương trình có nghiệm dương nhỏ nhất bằng 
.
d) Số nghiệm của phương trình trong khoảng 
là hai nghiệm.
Đáp án:
a – Đ b – S c – Đ d - S
Câu 6. Cho phương trình lượng giác 
:
a) Phương trình tương đương 
.
b) Đồ thị hàm số 
cắt trục hoành tại gốc tọa độ.
c) Phương trình có nghiệm là: 
.
d) Trên khoảng 
phương trình đã cho có một nghiệm.
Đáp án:
a – Đ b – Đ c – Đ d - S
Câu 7. Cho phương trình lượng giác 
:
a) Phương trình hoành độ giao điểm của hai đồ thị hàm số là: 
.
b) Hoành độ giao điểm của hai đồ thị là 
.
c) Khi 
thì hai đồ thị hàm số cắt nhau tại ba điểm.
d) Khi 
thì tọa độ giao điểm của hai đồ thị hàm số là 
.
Đáp án:
a – Đ b – Đ c – S d - S
Câu 8. Một vật dao động xung quanh vị trí cân bằng theo phương trình 
; trong đó 
là thời gian được tính bằng giây và quãng đường 
được tính bằng mét là khoảng cách theo phương ngang của chất điểm đối với vị trí cân bằng.
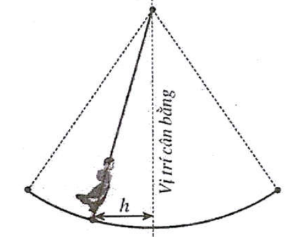
a) Vật ở xa vị trí cân bằng nhất nghĩa là 
.
b) Trong 10 giây đầu tiên, có hai thời điểm vật ở xa vị trí cân bằng nhất.
c) Khi vật ở vị trí cân bằng thì 
.
d) Trong khoảng từ 0 đến 20 giây thì vật đi qua vị trí cân bằng 4 lần.
Đáp án:
a – Đ b – S c – Đ d - S
Câu 9. Cho phương trình 
(*).
a) Điều kiện: 
.
b) Phương trình (*) có chung tập nghiệm với phương trình 
.
c) Gọi 
là nghiệm của phương trình (*), khi đó 
.
d) Nghiệm của phương trình (*) là hoành độ giao điểm của đường thẳng 
với 
.
Đáp án:
a – Đ b – S c – S d - S
Câu 10. Cho phương trình 
.
a) Điều kiện: 
.
b) Phương trình đã cho có chung tập nghiệm với phương trình 
.
c) Tổng các nghiệm của phương trình bằng 3.
d) Biết phương trình có hai nghiệm 
. Khi đó 3 số 
tạo thành một cấp số cộng.
Đáp án:
a – S b – S c – Đ d - Đ
-------------------- Vẫn còn tiếp --------------------
III. CÂU HỎI TRẮC NGHIỆM TRẢ LỜI NGẮN
Câu 1. Tìm số điểm biểu diễn tất cả các nghiệm của phương trình 
trên đường tròn lượng giác.
Đáp án: 2
Câu 2. Nghiệm dương nhỏ nhất của phương trình 
có dạng 
với 
là các số nguyên và nguyên tố cùng nhau. Tính tổng 
.
Đáp án: 17
Câu 3. Chiều cao 
của một cabin trên vòng quay vào thời điểm 
giây sau khi bắt đầu chuyển động được cho bởi công thức 
. Sau bao nhiêu giây thì cabin đạt độ cao 40 m lần đầu tiên?
Đáp án: 12,5
Câu 4. Một quả bóng được ném xiên một góc 
từ mặt đất với tốc độ 
. Khoảng cách theo phương ngang từ vị trí ban đầu của quả bóng đến vị trí bóng chạm đất được tính bởi công thức 
. Tính khoảng cách 
khi bóng được ném đi với tốc độ ban đầu 10 m/s và góc ném là 
so với phương ngang (làm tròn đến hàng phần trăm).
Đáp án: 8,66
Câu 5. Một vật 
được gắn vào đầu lò xo và dao động quanh vị trí cân bằng 
, biết rằng 
là hình chiếu vuông góc của 
trên trục 
, tọa độ điểm 
trên 
tại thời điểm 
(giây) là đại lượng 
(đơn vị: cm) được tính bởi công thức 
. Có bao nhiêu thời điểm trong khoảng 2 giây đầu tiên thì 
?
Đáp án: 5
-------------------- Vẫn còn tiếp --------------------
