Giáo án kì 2 Toán 12 cánh diều
Đầy đủ giáo án kì 2, giáo án cả năm Toán 12 cánh diều. Bộ giáo án chất lượng, chỉn chu, được hỗ trợ tốt nhất hiện nay. Khi mua giáo án được tặng thêm: bộ phiếu trắc nghiệm, bộ đề kiểm tra theo cấu trúc mới. Giáo án được gửi ngay và luôn. Có thể xem trước bất kì bài nào phía dưới trước khi mua.
Một số tài liệu quan tâm khác
Phần trình bày nội dung giáo án
I. GIÁO ÁN WORD KÌ 2 TOÁN 12 CÁNH DIỀU
- Giáo án Toán 12 cánh diều Bài 1: Nguyên hàm
- Giáo án Toán 12 cánh diều Bài 2: Nguyên hàm của một số hàm số sơ cấp
- Giáo án Toán 12 cánh diều Bài 3: Tích phân
- Giáo án Toán 12 cánh diều Bài 4: Ứng dụng hình học của tích phân
- Giáo án Toán 12 cánh diều Bài tập cuối chương IV
- Giáo án Toán 12 cánh diều Hoạt động thực hành và trải nghiệm Chủ đề 2: Thực hành tạo đồng hồ Mặt trời
- Giáo án Toán 12 cánh diều Bài 1: Phương trình mặt phẳng
- Giáo án Toán 12 cánh diều Bài 2: Phương trình đường thẳng
- Giáo án Toán 12 cánh diều Bài 3: Phương trình mặt cầu
- Giáo án Toán 12 cánh diều Bài tập cuối chương V
- Giáo án Toán 12 cánh diều Bài 1: Xác suất có điều kiện
- Giáo án Toán 12 cánh diều Bài 2: Công thức xác suất toàn phần. Công thức Bayes
- Giáo án Toán 12 cánh diều Bài tập cuối chương VI
- Giáo án Toán 12 cánh diều Bài Thực hành phần mềm GeoGebra
Ngày soạn:.../.../...
Ngày dạy:.../.../...
CHƯƠNG V: PHƯƠNG TRÌNH MẶT PHẲNG, ĐƯỜNG THẲNG, MẶT CẦU TRONG KHÔNG GIAN
BÀI 1: PHƯƠNG TRÌNH MẶT PHẲNG (5 TIẾT)
I. MỤC TIÊU
1. Về kiến thức
Sau bài học này, HS sẽ:
Nhận biết được phương trình mặt phẳng.
Viết phương trình mặt phẳng trong các trường hợp: qua một điểm và biết vectơ pháp tuyến, qua một điểm và biết cặp vectơ chỉ phương, qua ba điểm không thẳng hàng.
Nhận biết hai mặt phẳng song song, hai mặt phẳng vuông góc.
Tính khoảng cách từ một điểm đến một mặt phẳng.
Vận dụng kiến thức về phương trình mặt phẳng, công thức tính khoảng cách từ một điểm đến một mặt phẳng vào một số bài toán liên quan đến thực tiễn.
2. Về năng lực
Năng lực chung:
Năng lực tự chủ và tự học: Chủ động tìm tòi, khám phá kiến thức mới.
Năng lực giao tiếp và hợp tác: Có thái độ tôn trọng thầy cô, bạn bè trong trong bày, thảo luận và làm việc nhóm.
Năng lực giải quyết vấn đề và sáng tạo: Giải quyết được các vấn đề trong thực tiễn một cách sáng tạo.
Năng lực riêng:
Năng lực tư duy và lập luận toán học: So sánh, phân tích dữ liệu, phân tích, lập luận để giải thích được khái niệm phương trình mặt phẳng.
Năng lực mô hình hóa toán học: Xác định được điểm, biểu diễn được vectơ xuất hiện trong bài toán thực tiễn.
Năng lực giải quyết vấn đề toán học: Tính khoảng cách từ một điểm đến một mặt phẳng.
Năng lực giao tiếp toán học: Đọc, hiểu thông tin toán học.
Năng lực sử dụng công cụ, phương tiện học toán: Sử dụng được máy tính cầm tay.
3. Về phẩm chất
Chăm chỉ: Chủ động, kiên trì thực hiện nhiệm vụ thu thập các dữ liệu để khám phá vấn đề.
Trung thực: Có ý thức báo cáo các kết quả đã thu thập chính xác, khách quan.
Trách nhiệm: Tự giác hoàn thành công việc thu thập các dữ liệu bản thân được phân công, phối hợp với thành viên trong nhóm để hoàn thành nhiệm vụ.
II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU
1. Đối với GV: SGK, Tài liệu giảng dạy, giáo án, đồ dùng dạy học.
2. Đối với HS: SGK, SBT, vở ghi, giấy nháp, đồ dùng học tập (bút, thước...), bảng nhóm, bút viết bảng nhóm.
III. TIẾN TRÌNH DẠY HỌC
A. HOẠT ĐỘNG KHỞI ĐỘNG (MỞ ĐẦU)
a) Mục tiêu:
- Tạo hứng thú, thu hút HS tìm hiểu nội dung bài học.
b) Nội dung: HS đọc tình huống mở đầu, suy nghĩ trả lời câu hỏi.
c) Sản phẩm: HS đưa ra được nhận định ban đầu về câu hỏi mở đầu.
d) Tổ chức thực hiện:
Bước 1: Chuyển giao nhiệm vụ:
- GV yêu cầu HS đọc tình huống mở đầu:
Người ta muốn sản xuất một chi tiết máy được cắt ra từ một ống trụ thép gia công cơ khí chính xác (Hình 1). Để làm chi tiết máy đó, người ta cần xác định phương trình của mặt cắt trong một hệ tọa độ thích hợp và đưa những dữ liệu đó vào hệ thống máy tính điều khiển các máy gia công cơ khí kĩ thuật số. |
|
Trong không gian vơi hệ tọa độ ![]() , phương trình của mặt phẳng là gì?
, phương trình của mặt phẳng là gì?
Làm thế nào để lập được phương trình của mặt phẳng?
Bước 2: Thực hiện nhiệm vụ: HS quan sát và chú ý lắng nghe, thảo luận nhóm đôi hoàn thành yêu cầu.
Bước 3: Báo cáo, thảo luận: GV gọi một số HS trả lời, HS khác nhận xét, bổ sung.
Bước 4: Kết luận, nhận định: GV đánh giá kết quả của HS, trên cơ sở đó dẫn dắt HS vào bài học mới: “Trong chương này, chúng ta sẽ tìm hiểu những nội dung sau: phương trình mặt phẳng trong không gian; phương trình đường thẳng trong không gian; phương trình mặt cầu trong không gian. Hôm nay chúng ta sẽ học đơn vị kiến thức đầu tiên, phương trình mặt phẳng.”.
Bài mới: Phương trình mặt phẳng.
B. HÌNH THÀNH KIẾN THỨC MỚI
Hoạt động 1: Vectơ pháp tuyến. Cặp vectơ chỉ phương của mặt phẳng
a) Mục tiêu:
Nhận biết được vectơ pháp tuyến, vectơ chỉ phương của mặt phẳng.
b) Nội dung:
HS đọc SGK, nghe giảng, thực hiện các nhiệm vụ được giao, suy nghĩ trả lời câu hỏi, thực hiện các HĐ1, 2, 3, Luyện tập 1; 2; 3 và các ví dụ.
c) Sản phẩm: HS hình thành được kiến thức bài học, câu trả lời của HS cho các câu hỏi. HS nhận biết khái niệm vectơ pháp tuyến, vectơ chỉ phương.
d) Tổ chức thực hiện:
HĐ CỦA GV VÀ HS | SẢN PHẨM DỰ KIẾN |
Bước 1: Chuyển giao nhiệm vụ:
- HS trả lời HĐ1.
- GV dẫn dắt:
- GV đặt câu hỏi: Một mặt phẳng có bao nhiêu vectơ pháp tuyến? Từ đó dẫn đến nhận xét. - GV cho HS thực hiện Ví dụ 1: Vectơ nào vuông góc với mặt phẳng - HS thực hiện Luyện tập 1.
- HS trả lời HĐ2.
- GV giới thiệu cho HS khái niệm cặp vectơ chỉ phương.
- HS tìm hiểu Ví dụ 2.
- HS thực hiện Luyện tập 2:
- HS thảo luận nhóm đôi, hoàn thành HĐ3. + Tìm vectơ + Vectơ
- GV đưa công thức xác định vectơ pháp tuyến từ tích có hướng của hai cặp vectơ chỉ phương.
Bước 2: Thực hiện nhiệm vụ: - HS theo dõi SGK, chú ý nghe, tiếp nhận kiến thức, hoàn thành các yêu cầu, thảo luận nhóm. - GV quan sát hỗ trợ. Bước 3: Báo cáo, thảo luận: - HS giơ tay phát biểu, lên bảng trình bày - Một số HS khác nhận xét, bổ sung cho bạn. Bước 4: Kết luận, nhận định: GV tổng quát lưu ý lại kiến thức trọng tâm và yêu cầu HS ghi chép đầy đủ vào vở. | I. Vectơ pháp tuyến. Cặp vectơ chỉ phương của mặt phẳng 1. Vectơ pháp tuyến HĐ1:
Giá của vectơ Vì Vậy giá của vectơ Khái niệm Cho mặt phẳng
Vectơ Nhận xét: Nếu Ví dụ 1 (SGK -tr.51) Hướng dẫn giải: SGK – tr.51
Luyện tập 1
a) Vectơ b) Vectơ 2. Cặp vectơ chỉ phương HĐ2
+ Vì + Vì + Vì Kết luận Cho mặt phẳng Ví dụ 2 (SGK -tr.51) Hướng dẫn giải: SGK – tr.52 Luyện tập 2
+ Do hai vectơ + Do hai vectơ + Do hai vectơ 3. Xác định vectơ pháp tuyến của mặt phẳng khi biết cặp vectơ chỉ phương HĐ3
a) Xét vectơ
Vậy b) Vì Suy ra giá của vectơ Mà Kết luận Nếu hai vectơ Ví dụ 3 (SGK -tr.52) Hướng dẫn giải: SGK – tr.52 Luyện tập 3 Ta có Do đó vectơ
|
--------------------------------------
--------------------- Còn tiếp ----------------------
Ngày soạn:.../.../...
Ngày dạy:.../.../...
CHƯƠNG V: PHƯƠNG TRÌNH MẶT PHẲNG, ĐƯỜNG THẲNG, MẶT CẦU TRONG KHÔNG GIAN
BÀI 2: PHƯƠNG TRÌNH ĐƯỜNG THẲNG (5 TIẾT)
I. MỤC TIÊU
1. Về kiến thức
Sau bài học này, HS sẽ:
Nhận biết được các phương trình tham số, chính tắc của đường thẳng.
Viết được phương trình đường thẳng đi qua một điểm và biết vectơ chỉ phương.
Viết được phương trình đường thẳng đi qua hai điểm.
Nhận biết vị trí tương đối của hai đường thẳng.
Vận dụng kiến thức về phương trình đường thẳng, vị trí tương đối về phương trình đường thẳng, vị trí tương đối giữa hai đường thẳng vào một số bài toán liên quan đến thực tiễn.
Tính góc giữa hai đường thẳng, góc giữa đường thẳng với mặt phẳng, góc giữa hai mặt phẳng.
Vận dụng kiến thức về góc vào một số bài toán liên quan đến thực tiễn.
2. Về năng lực
Năng lực chung:
Năng lực tự chủ và tự học: Chủ động tìm tòi, khám phá kiến thức mới.
Năng lực giao tiếp và hợp tác: Có thái độ tôn trọng thầy cô, bạn bè trong trong bày, thảo luận và làm việc nhóm.
Năng lực giải quyết vấn đề và sáng tạo: Giải quyết được các vấn đề trong thực tiễn một cách sáng tạo.
Năng lực riêng:
Tư duy và lập luận toán học: So sánh, phân tích dữ liệu, phân tích, lập luận để giải thích được khái niệm được các phương trình tham số, chính tắc của đường thẳng.
Mô hình hóa toán học: mô tả các dữ kiện bài toán thực tế, giải quyết bài toán liên quan đến phương trình đường thẳng và góc trong không gian.
Giải quyết vấn đề toán học: viết được phương trình đường thẳng, xác định được vị trí tương đối của hai đường thẳng trong không gian; Tính góc giữa hai đường thẳng, góc giữa đường thẳng với mặt phẳng, góc giữa hai mặt phẳng.
Giao tiếp toán học: đọc, hiểu thông tin toán học.
3. Về phẩm chất
Chăm chỉ: Chủ động, kiên trì thực hiện nhiệm vụ thu thập các dữ liệu để khám phá vấn đề.
Trung thực: Có ý thức báo cáo các kết quả đã thu thập chính xác, khách quan.
Trách nhiệm: Tự giác hoàn thành công việc thu thập các dữ liệu bản thân được phân công, phối hợp với thành viên trong nhóm để hoàn thành nhiệm vụ.
II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU
1. Đối với GV: SGK, Tài liệu giảng dạy, giáo án, đồ dùng dạy học, laptop, ppt.
2. Đối với HS: SGK, SBT, vở ghi, giấy nháp, đồ dùng học tập (bút, thước...), bảng nhóm, bút viết bảng nhóm.
III. TIẾN TRÌNH DẠY HỌC
A. HOẠT ĐỘNG KHỞI ĐỘNG (MỞ ĐẦU)
a) Mục tiêu: Gợi động cơ, tạo hứng thú, thu hút HS tìm hiểu nội dung bài học.
b) Nội dung: HS đọc tình huống mở đầu, suy nghĩ trả lời câu hỏi về tọa độ của vectơ.
c) Sản phẩm: HS đưa ra được nhận định ban đầu về câu hỏi mở đầu.
d) Tổ chức thực hiện:
Bước 1: Chuyển giao nhiệm vụ:
- GV yêu cầu HS đọc tình huống mở đầu:
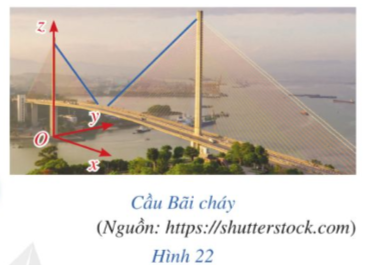
Cầu Bãi Cháy nối Hòn Gai và Bãi Cháy (Quảng Ninh). Dây cáp của cầu gợi nên hình ảnh đường thẳng trong không gian với hệ tọa độ |
|
Trong hệ tọa độ ![]() , phương trình của đường thẳng là gì? Làm thế nào để lập được phương trình đường thẳng?
, phương trình của đường thẳng là gì? Làm thế nào để lập được phương trình đường thẳng?
Bước 2: Thực hiện nhiệm vụ: HS quan sát và chú ý lắng nghe, thảo luận nhóm đôi hoàn thành yêu cầu.
Bước 3: Báo cáo, thảo luận: GV gọi một số HS trả lời, HS khác nhận xét, bổ sung.
Bước 4: Kết luận, nhận định: GV đánh giá kết quả của HS, trên cơ sở đó dẫn dắt HS vào bài học mới: “Để viết phương trình đường thẳng trong ![]() thì chúng ta cần biết vectơ chỉ phương và một điểm thuộc đường thẳng đó. Phương trình đường thẳng trong không gian có giống như vậy không, bài học hôm nay sẽ trả lời câu hỏi đó.”.
thì chúng ta cần biết vectơ chỉ phương và một điểm thuộc đường thẳng đó. Phương trình đường thẳng trong không gian có giống như vậy không, bài học hôm nay sẽ trả lời câu hỏi đó.”.
Bài mới: Phương trình đường thẳng.
B. HÌNH THÀNH KIẾN THỨC MỚI
Hoạt động 1: Phương trình đường thẳng
a) Mục tiêu:
Nhận biết vectơ chỉ phương của đường thẳng.
Nhận biết được các phương trình tham số, chính tắc của đường thẳng.
Viết được phương trình đường thẳng đi qua một điểm và biết vectơ chỉ phương.
Viết được phương trình đường thẳng đi qua hai điểm.
b) Nội dung:
HS đọc SGK, nghe giảng, thực hiện các nhiệm vụ được giao, suy nghĩ trả lời câu hỏi, thực hiện các HĐ1, 2,3, 4 Luyện tập 1; 2; 3, 4 và các ví dụ.
c) Sản phẩm: HS hình thành được kiến thức bài học, câu trả lời của HS cho các câu hỏi. HS nhận biết và viết được phương trình đường thẳng.
d) Tổ chức thực hiện:




--------------------------------------
--------------------- Còn tiếp ----------------------
II. TRẮC NGHIỆM KÌ 2 TOÁN 12 CÁNH DIỀU
- Phiếu trắc nghiệm Toán 12 cánh diều Bài 1: Nguyên hàm
- Phiếu trắc nghiệm Toán 12 cánh diều Bài 2: Nguyên hàm của một số hàm số sơ cấp
- Phiếu trắc nghiệm Toán 12 cánh diều Bài 3: Tích phân
- Phiếu trắc nghiệm Toán 12 cánh diều Bài 4: Ứng dụng hình học của tích phân
- Phiếu trắc nghiệm Toán 12 cánh diều Bài tập cuối chương IV
- Phiếu trắc nghiệm Toán 12 cánh diều Hoạt động thực hành và trải nghiệm Chủ đề 2: Thực hành tạo đồng hồ Mặt trời
- Phiếu trắc nghiệm Toán 12 cánh diều Bài 1: Phương trình mặt phẳng
- Phiếu trắc nghiệm Toán 12 cánh diều Bài 2: Phương trình đường thẳng
- Phiếu trắc nghiệm Toán 12 cánh diều Bài 3: Phương trình mặt cầu
- Phiếu trắc nghiệm Toán 12 cánh diều Bài tập cuối chương V
- Phiếu trắc nghiệm Toán 12 cánh diều Bài 1: Xác suất có điều kiện
- Phiếu trắc nghiệm Toán 12 cánh diều Bài 2: Công thức xác suất toàn phần. Công thức Bayes
- Phiếu trắc nghiệm Toán 12 cánh diều Bài tập cuối chương VI
CHƯƠNG IV. NGUYÊN HÀM. TÍCH PHÂN
BÀI 1: NGUYÊN HÀM
A. TRẮC NGHIỆM NHIỀU ĐÁP ÁN LỰA CHỌN
1. NHẬN BIẾT (6 CÂU)
Câu 1: Mệnh đề nào sau đây sai?
A. Nếu ![]() là một nguyên hàm của
là một nguyên hàm của ![]() trên
trên ![]() và
và ![]() là hằng số thì
là hằng số thì ![]() .
.
B. Mọi hàm số liên tục trên ![]() đều có nguyên hàm trên
đều có nguyên hàm trên ![]() .
.
C. ![]() là một nguyên hàm của
là một nguyên hàm của ![]() trên
trên ![]() .
.
D. ![]()
Câu 2: Cho hai hàm số ![]() là hàm số liên tục, có
là hàm số liên tục, có ![]() lần lượt là nguyên hàm của
lần lượt là nguyên hàm của ![]() . Xét các mệnh đề sau:
. Xét các mệnh đề sau:
(I) ![]() là một nguyên hàm của
là một nguyên hàm của ![]()
(II) ![]() là một nguyên hàm của
là một nguyên hàm của ![]() .
.
(III) ![]() là một nguyên hàm của
là một nguyên hàm của ![]()
Số mệnh đề đúng là:
A. 1.
B. ![]()
C. ![]()
D. ![]() .
.
Câu 3: Trong các khẳng định sau, khẳng định nào sai?
A. ![]()
B. Nếu ![]() và
và ![]() đều là nguyên hàm của hàm số
đều là nguyên hàm của hàm số ![]() thì
thì ![]() là hằng số.
là hằng số.
C. ![]() là một nguyên hàm của
là một nguyên hàm của ![]() .
.
D. ![]() là một nguyên hàm của
là một nguyên hàm của ![]() .
.
Câu 4: Mệnh đề nào sau đây sao?
A. ![]() với mọi hằng số
với mọi hằng số ![]() và với mọi hàm số
và với mọi hàm số ![]() liên tục trên
liên tục trên ![]() .
.
B. ![]() , với mọi hàm số
, với mọi hàm số ![]() liên tục trên
liên tục trên ![]() .
.
C. ![]() , với mọi hàm số
, với mọi hàm số ![]() liên tục trên
liên tục trên ![]() .
.
D. ![]() với mọi hàm số
với mọi hàm số ![]() có đạo hàm trên
có đạo hàm trên ![]() .
.
Câu 5: Cho hàm số ![]() xác định trên
xác định trên ![]() và
và ![]() là một nguyên hàm của
là một nguyên hàm của ![]() trên
trên ![]() . Khẳng định nào dưới đây đúng?
. Khẳng định nào dưới đây đúng?
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Câu 6: Cho hàm số ![]() xác định trên
xác định trên ![]() . Khẳng định nào sau đây sai?
. Khẳng định nào sau đây sai?
A. Nếu hàm số ![]() là một nguyên hàm của
là một nguyên hàm của ![]() trên
trên ![]() thì với mỗi hằng số
thì với mỗi hằng số ![]() , hàm số
, hàm số ![]() cũng là một nguyên hàm của
cũng là một nguyên hàm của ![]() trên
trên ![]() .
.
B. Hàm số ![]() được gọi là một nguyên hàm của
được gọi là một nguyên hàm của ![]() trên
trên ![]() nếu
nếu ![]() với mọi
với mọi ![]() .
.
C. Nếu hàm số ![]() là một nguyên hàm của
là một nguyên hàm của ![]() trên
trên ![]() thì hàm số
thì hàm số ![]() là một nguyên hàm của
là một nguyên hàm của ![]() trên
trên ![]() .
.
D. Nếu ![]() liên tục trên
liên tục trên ![]() thì nó có nguyên hàm trên
thì nó có nguyên hàm trên ![]() .
.
2. THÔNG HIỂU (10 CÂU)
Câu 1: Họ nguyên hàm của hàm số ![]() là:
là:
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Câu 2: Nguyên hàm của hàm số ![]() là:
là:
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]()
Câu 3: Cho hàm số ![]() . Khẳng định nào dưới đây đúng?
. Khẳng định nào dưới đây đúng?
A. ![]()
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Câu 4: Tìm nguyên hàm của hàm số ![]()
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
--------------------------------------
--------------------- Còn tiếp ----------------------
CHƯƠNG V. PHƯƠNG TRÌNH MẶT PHẲNG. ĐƯỜNG THẲNG. MẶT CẦU TRONG KHÔNG GIAN
BÀI 3: PHƯƠNG TRÌNH MẶT CẦU
A. TRẮC NGHIỆM NHIỀU ĐÁP ÁN LỰA CHỌN
1. NHẬN BIẾT (10 CÂU)
Câu 1: Phương trình nào sau đây là phương trình mặt cầu?
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Câu 2: Phương trình nào sau đây không phải là phương trình mặt cầu?
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Câu 3: Trong không gian ![]() , cho mặt cầu
, cho mặt cầu ![]() . Tâm của
. Tâm của ![]() có tọa độ là:
có tọa độ là:
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Câu 4: Trong không gian ![]() , cho mặt cầu
, cho mặt cầu ![]() . Bán kính của
. Bán kính của ![]() bằng:
bằng:
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Câu 5: Trong không gian với hệ trục tọa độ ![]() , cho mặt cầu
, cho mặt cầu ![]() . Bán kính của mặt cầu đã cho bằng:
. Bán kính của mặt cầu đã cho bằng:
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Câu 6: Trong không gian với hệ trục tọa độ ![]() , cho mặt cầu
, cho mặt cầu ![]() . Tìm tọa độ tâm và bán kính của mặt cầu
. Tìm tọa độ tâm và bán kính của mặt cầu ![]() .
.
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Câu 7: Trong không gian hệ tọa độ ![]() , cho mặt cầu
, cho mặt cầu ![]() có tâm
có tâm ![]() và đi qua điểm
và đi qua điểm ![]() . Phương trình của
. Phương trình của ![]() là:
là:
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Câu 8: Trong không gian với hệ trục tọa độ ![]() , tìm tất cả các giá trị của
, tìm tất cả các giá trị của ![]() để phương trình
để phương trình ![]() là phương trình của một mặt cầu.
là phương trình của một mặt cầu.
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Câu 9: Phương trình nào dưới đây là phương trình của một mặt cầu?
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Câu 10: Trong không gian với hệ trục tọa độ ![]() , cho mặt cầu
, cho mặt cầu ![]() có đường kính
có đường kính ![]() với
với ![]() . Tìm tọa độ tâm
. Tìm tọa độ tâm ![]() và bán kính
và bán kính ![]() của mặt cầu.
của mặt cầu.
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
2. THÔNG HIỂU (10 CÂU)
Câu 1: Trong không gian với hệ trục tọa độ ![]() , cho hai điểm
, cho hai điểm ![]() và
và ![]() . Phương trình mặt cầu có đường kính
. Phương trình mặt cầu có đường kính ![]() là:
là:
A. ![]()
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
--------------------------------------
--------------------- Còn tiếp ----------------------

Hệ thống có đủ tài liệu:
- Giáo án toán 12 cánh diều (295k)
- Giáo án chuyên đề toán 12 cánh diều (295k)
- Giáo án Powerpoint Toán 12 Cánh diều (340k)
- Giáo án dạy thêm toán 12 cánh diều (295k)
- Giáo án powerpoint chuyên đề toán 12 cánh diều (340k)
- Câu hỏi và bài tập trắc nghiệm Toán 12 cánh diều (150k)
- Giáo án powerpoint dạy thêm toán 12 cánh diều (340k)
- File word đáp án Toán 12 cánh diều (100k)
- Đề thi Toán 12 Cánh diều (150k)
- Kiến thức trọng tâm Toán 12 cánh diều (150k)
- Phiếu học tập theo bài Toán 12 cánh diều cả năm (150k)
- Trắc nghiệm đúng sai Toán 12 cánh diều cả năm (150k)
- Bài tập file word Toán 12 cánh diều (150k)
- Trắc nghiệm dạng câu trả lời ngắn Toán 12 cánh diều cả năm (150k)
=> Có thể chọn nâng cấp VIP với phí là 850k để tải tất cả tài liệu ở trên
- Chỉ gửi 550k. Tải về dùng thực tế, 1 ngày sau mới gửi số còn lại.
Cách tải hoặc nâng cấp:
- Bước 1: Chuyển phí vào STK: 1214136868686 - cty Fidutech - MB
- Bước 2: Nhắn tin tới Zalo Fidutech - nhấn vào đây để thông báo và nhận tài liệu