Giáo án ppt kì 2 Toán 12 chân trời sáng tạo

I. SLIDE ĐIỆN TỬ KÌ 2 TOÁN 12 CHÂN TRỜI SÁNG TẠO

• Giáo án điện tử Toán 12 chân trời Bài 1: Nguyên hàm
• Giáo án điện tử Toán 12 chân trời Bài 2: Tích phân
• Giáo án điện tử Toán 12 chân trời Bài 3: Ứng dụng hình học của tích phân
• Giáo án điện tử Toán 12 chân trời Bài tập cuối chương IV
• Giáo án điện tử Toán 12 chân trời Bài 1: Phương trình mặt phẳng
• Giáo án điện tử Toán 12 chân trời Bài 1: Phương trình mặt phẳng (P2)
• Giáo án điện tử Toán 12 chân trời Bài 2: Phương trình đường thẳng trong không gian
• Giáo án điện tử Toán 12 chân trời Bài 2: Phương trình đường thẳng trong không gian (P2)
• Giáo án điện tử Toán 12 chân trời Bài 2: Phương trình đường thẳng trong không gian (P3)
• Giáo án điện tử Toán 12 chân trời Bài 3: Phương trình mặt cầu
• Giáo án điện tử Toán 12 chân trời Bài tập cuối chương V
• Giáo án điện tử Toán 12 chân trời Bài 1: Xác suất có điều kiện
• Giáo án điện tử Toán 12 chân trời Bài 2: Công thức xác suất toàn phần và công thức Bayes
• Giáo án điện tử Toán 12 chân trời Bài tập cuối chương VI
• Giáo án điện tử Toán 12 chân trời Hoạt động thực hành và trải nghiệm Bài 1: Tính giá trị gần đúng tích phân bằng máy tính cầm tay
• Giáo án điện tử Toán 12 chân trời Hoạt động thực hành và trải nghiệm Bài 2: Minh hoạ và tính tích phân bằng phần mềm GeoGebra
• Giáo án điện tử Toán 12 chân trời Hoạt động thực hành và trải nghiệm Bài 3: Sử dụng phần mềm GeoGebra để biểu diễn hình học toạ độ trong không gian

CHÀO MỪNG CÁC EM ĐẾN VỚI TIẾT HỌC!

KHỞI ĐỘNG

Một ô tô đang di chuyển với vận tốc thì hãm phanh nên tốc độ của xe thay đổi theo thời gian (giây) được tính theo công thức 

Kể từ khi hãm phanh đến khi dừng, ô tô đi được quãng đường bao nhiêu?

CHƯƠNG IV: 

NGUYÊN HÀM. TÍCH PHÂN

BÀI 2: TÍCH PHÂN

NỘI DUNG BÀI HỌC 

1 DIỆN TÍCH HÌNH THANG CONG

HĐKP1

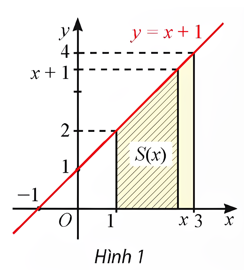
Cho hàm số . Với mỗi , kí hiệu là diện tích của hình thang giới hạn bởi đồ thị hàm số trục hoành và hai đường thằng vuông góc với tại các điểm có hoành độ và .

a) Tính .

b) Tính với mỗi

c) Tính Từ đó suy ra là một nguyên hàm của trên

d) Cho là một nguyên hàm của hàm số . Chứng tỏ rằng Từ đó nhận xét về cách tính khi biết một nguyên hàm của

Giải:

c) với mọi . 

Từ đó, là một nguyên hàm của hàm số .

Vậy có thể tính bởi khi biết một nguyên hàm của .

Kết luận

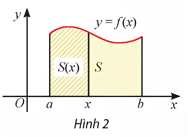
Cho hàm số liên tục và không âm trên đoạn . Hình phẳng giới hạn bởi đồ thị hàm số , trục hoành và hai đường thẳng được gọi là hình thang cong.

- Nếu hàm số liên tục và không âm trên đoạn thì diện tích của hình thang cong giới hạn bởi đồ thị hàm số , trục hoành và hai đường thẳng được tính bởi trong đó là một nguyên hàm của trên đoạn .

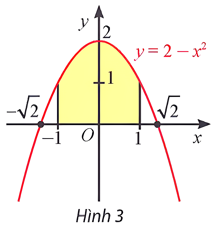
Ví dụ 1:Tính diện tích hình thang cong giới hạn bởi đồ thị hàm số , trục hoành và hai đường thẳng (Hình 3).

Giải:

Hàm số liên tục, dương trên đoạn và có một nguyên hàm là 

Do đó, diện tích hình thang cong cần tìm là

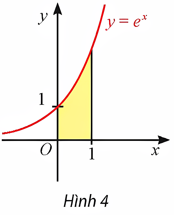
Thực hành 1

Tính diện tích hình thang cong giới hạn bởi đồ thị hàm số trục hoành, trục tung và đường thẳng (Hình 4).

Giải:

Ta có hàm số liên tục, nhận giá trị dương trên và có một nguyên hàm là . 

Do đó, diện tích hình thang cong cần tìm là 

.

2 KHÁI NIỆM TÍCH PHÂN

HĐKP2

Cho hàm số . Lấy hai nguyên hàm tuỳ ý và của rồi tính và Nhận xét về kết quả nhận được.

Giải:

Chẳng hạn lấy và .

Ta có

         .

Vậy .

Kết luận

Cho hàm số liên tục trên đoạn . Nếu là một nguyên hàm của trên đoạn thì hiệu số được gọi là tích phân từ đến của hàm số , kí hiệu .

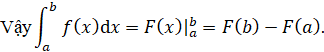
Ta gọi là dấu tích phân, và là cận tích phân, là cận dưới, là cận trên, là biểu thức dưới dấu tích phân và là hàm số dưới dấu tích phân.

Chú ý:

a) Trong trường hợp hoặc , ta quy ước

b) Người ta chứng minh được rằng, tích phân chỉ phụ thuộc vào hàm số và các cận mà không phụ thuộc vào biến số hay , 

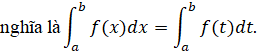
c) Ý nghĩa hình học của tích phân

Nếu hàm số liên tục và không âm trên đoạn thì là diện tích của hình thang cong giới hạn bởi đồ thị hàm số , trục hoành và hai đường thẳng , .

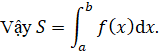
Ví dụ 2:Tính các tích phân sau:

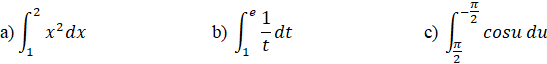
------------------------- Còn tiếp -------------------------

CHÀO MỪNG CẢ LỚP ĐÃ ĐẾN VỚI BÀI HỌC HÔM NAY!

KHỞI ĐỘNG

Ta đã biết trong mặt phẳng phương trình tham số của đường thẳng có dạng:

Trong không gian , phương trình tham số của đường thẳng có dạng như thế nào?

CHƯƠNG V: 

PHƯƠNG TRÌNH MẶT PHẲNG, ĐƯỜNG THẲNG, MẶT CẦU

BÀI 2: PHƯƠNG TRÌNH 

ĐƯỜNG THẲNG TRONG KHÔNG GIAN

NỘI DUNG BÀI HỌC

1. Phương trình đường thẳng trong không gian
2. Vị trí tương đối giữa hai đường thẳng. Điều kiện để hai đường thẳng       vuông góc
3. Góc

1. PHƯƠNG TRÌNH ĐƯỜNG THẲNG TRONG KHÔNG GIAN

Vectơ chỉ phương của đường thẳng

• HĐKP 1: Trong không gian , cho điểm cố định và vectơ khác 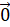. Có bao nhiêu đường thẳng 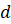đi qua 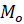và song song hoặc trùng với giá của ?

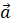Giải:

Có duy nhất một đường thẳng đi qua và song song hoặc trùng với giá của .

ĐỊNH NGHĨA

Vectơ khác có giá song song hoặc trùng với đường thẳng được gọi là vectơ chỉ phương của .

Chú ý: Nếu là vectơ chỉ phương của thì cũng là vectơ chỉ phương của .

Ví dụ 1. Trong không gian , cho hình chóp có , và

a) Tìm toạ độ một vectơ chỉ phương của mỗi đường thẳng .

b) Vectơ có là vectơ chỉ phương của đường thẳng không?

Giải:

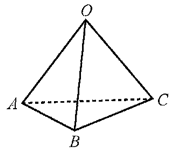
a) Ta có là một vectơ chỉ phương của đường thẳng

là một vectơ chỉ phương của đường thẳng

chỉ phương của đường thẳng .

Thực hành 1

Trong không gian , cho hình lăng trụ tam giác với . Tìm toạ độ một vectơ chỉ phương của mỗi đường thẳng và

Giải:

Đường thẳng có một vectơ chỉ phương là

Đường thẳng có một vectơ chỉ phương là

Đường thẳng có một vectơ chỉ phương là .

Phương trình tham số của đường thẳng

• HĐKP 2: Trong không gian , cho đường thằng đi qua điểm cố định và có vectơ chỉ phương là 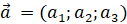khác .

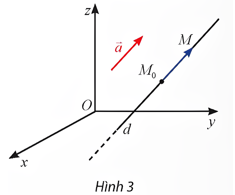
a) Giải thích tại sao ta có thể viết: 

b) Với thuộc , hãy tính theo và .

Giải:

a) Ta có: cùng phương với vectơ .

                cùng phương với vectơ nên .

b)

Vậy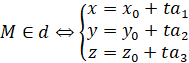

ĐỊNH NGHĨA

Trong không gian , phương trình tham số của đường thẳng đi qua điểm và nhận làm vectơ chỉ phương có dạng:

Ví dụ 2. Cho đường thẳng có phương trình tham số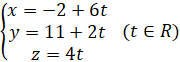

a) Tìm hai vectơ chỉ phương của .

b) Tìm các điểm trên ứng với lần lượt bằng

Giải:

a) Từ phương trình tham số, ta có là một vectơ chỉ phương của .

b) Thay vào phương trình tham số của , ta được:

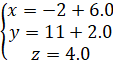 hay 

Vậy

Tương tự, với thì

                  với thì

Chú ý:

a) Trong phương trình tham số của đường thẳng

mỗi giá trị của tham số xác định duy nhất một điểm trên và ngược lại.

b) Từ nay để cho gọn, trong phương trình tham số của đường thẳng, ta không viết .

Ví dụ 3. Viết phương trình tham số của đường thẳng đi qua điểm và nhận làm vectơ chỉ phương. Đường thẳng có đi qua điểm không?

Giải:

Ta có phương trình tham số của là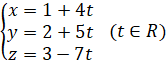

Thay vào phương trình , ta được , suy ra

Thay và vào phương trình , ta thấy phương trình không thoả mãn.

Suy ra đường thẳng không đi qua điểm .

Thực hành 2

------------------------- Còn tiếp -------------------------

II. BÀI TẬP TỰ LUẬN KÌ 2 TOÁN 12 CHÂN TRỜI SÁNG TẠO

• Bài tập file word Toán 12 chân trời Bài 1: Nguyên hàm
• Bài tập file word Toán 12 chân trời Bài 2: Tích phân
• Bài tập file word Toán 12 chân trời Bài 3: Ứng dụng hình học của tích phân
• Bài tập file word Toán 12 chân trời Bài 1: Phương trình mặt phẳng
• Bài tập file word Toán 12 chân trời Bài 2: Phương trình đường thẳng trong không gian
• Bài tập file word Toán 12 chân trời Bài 3: Phương trình mặt cầu
• Bài tập file word Toán 12 chân trời Bài 1: Xác suất có điều kiện
• Bài tập file word Toán 12 chân trời Bài 2: Công thức xác suất toàn phần và công thức Bayes

CHƯƠNG IV. NGUYÊN HÀM. TÍCH PHÂN

BÀI 3: ỨNG DỤNG HÌNH HỌC CỦA TÍCH PHÂN

(35 câu)

1. NHẬN BIẾT (15 CÂU)

Câu 1: Công thức tính diện tích hình phẳng giới hạn bởi hai đồ thị hàm số , liên tục trên  và hai đường thẳng , là?

Trả lời:

.

Câu 2: Diện tích hình phẳng giới hạn bởi các đường , . (Đơn vị diện tích)

Trả lời:

Đặt

(loại).

Bảng xét dấu

.

Câu 3: Diện tích hình phẳng giới hạn bởi là?

Trả lời:

Ta có

.

Vậy (đvdt).

Câu 4: Cho đồ thị hàm số . Diện tích hình phẳng (phần tô đậm trong hình) là?

Trả lời:

Theo định nghĩa ta có

Câu 5: Diện tích hình phẳng được giới hạn bởi đồ thị hàm số , trục hoành và hai đường thẳng , là?

Trả lời:

Ta có trên đoạn nên

Câu 6: Diện tích hình phẳng được giới hạn bởi đồ thị hàm số , trục hoành và hai đường thẳng , là?

Trả lời:

Ta có trên đoạn nên

Câu 7: Diện tích hình phẳng được giới hạn bởi đồ thị hàm số , trục hoành và hai đường thẳng , là?

Trả lời:

Ta có trên đoạn nên

Câu 8: Diện tích hình phẳng được giới hạn bởi đồ thị hàm số , trục hoành và hai đường thẳng , là?

Trả lời: 

Ta có trên đoạn nên

Câu 9: Diện tích hình phẳng được giới hạn bởi đồ thị hàm số , trục hoành và hai đường thẳng , là?

Trả lời: 

Ta có trên đoạn nên

Câu 10: Diện tích hình phẳng được giới hạn bởi đồ thị hàm số , trục hoành và hai đường thẳng , là?

Trả lời: 

Ta có trên đoạn nên

------------------------- Còn tiếp -------------------------

CHƯƠNG V. PHƯƠNG TRÌNH MẶT PHẲNG, ĐƯỜNG THẲNG, MẶT CẦU

BÀI 3: PHƯƠNG TRÌNH MẶT CẦU

(39 câu)

3. VẬN DỤNG (5 CÂU)

Câu 1: Viết phương trình mặt cầu (S) qua gốc O và các giao điểm của mặt phẳng với ba trục tọa độ.

Trả lời: 

cắt ba trục tại  

nên:

Vậy  

Câu 2: Cho mặt cầu và mặt phẳng . Gọi M là tiếp điểm của (S) và tiếp diện di động (Q) vuông góc với (P). tập hợp các điểm M là?

Trả lời: 

có tâm ,  bán kính IM vuông góc với , nên M nằm trong mặt phẳng qua I và song song với .

Phương trình  

Tập hợp các điểm M là đường tròn giao tuyến của và :

Câu 3: Cho mặt cầu và mặt phẳng . Viết phương trình mặt cầu (S’) có bán kính nhỏ nhất chứa giao tuyến của (S) và (P).

Trả lời: 

có bán kính nhỏ nhất Tâm

Vậy

Câu 4: Cho tứ diện ABCD có . Viết phương trình mặt cầu tiếp xúc với 6 cạnh của tứ diện.

Trả lời: 

;

.

Mặt cầy tiếp xúc với 6 cạnh tại trung điểm của chúng.

Gọi I và J là trung điểm của AB và CD  

có bán kính tâm  

Câu 5: Cho tứ diện ABCD có . Viết phương trình mặt cầu nội tiếp tứ diện.

Trả lời: 

Tứ diện ABCD đều.

tiếp xúc với bốn mặt của tứ diện tại trọng tâm của mỗi mặt.

Trọng tâm G của tam giác đều ACD: tâm của  

Bán kính của  

------------------------- Còn tiếp -------------------------