Kênh giáo viên » Trắc nghiệm dạng câu trả lời ngắn Toán 9 kết nối tri thức cả năm

Trắc nghiệm câu trả lời ngắn Toán 9 kết nối Bài 16: Vị trí tương đối của đường thẳng và đường tròn

Tài liệu trắc nghiệm dạng câu trả lời ngắn Toán 9 kết nối tri thức Bài 16: Vị trí tương đối của đường thẳng và đường tròn. Dựa trên kiến thức của bài học, bộ tài liệu được biên soạn chi tiết, đúng trọng tâm và rõ ràng. Câu hỏi đa dạng với các mức độ khó dễ khác nhau. Tài liệu có file Word tải về. Thời gian tới, nội dung này sẽ tiếp tục được bổ sung.

Xem: => Giáo án toán 9 kết nối tri thức

Tải về

BÀI 16: VỊ TRÍ TƯƠNG ĐỐI CỦA ĐƯỜNG THẲNG VÀ ĐƯỜNG TRÒN

Câu 1: Cho đường thẳng và một điểm cho các đường tròn sau:

i) Đường tròn

ii) Đường tròn

iii) Đường tròn

iv) Đường tròn

Có bao nhiêu đường tròn cắt đường thẳng

Câu 2: Cho đường thẳng và một điểm cách một khoảng . Vẽ đường tròn tâm , bán kính . Gọi và là các giao điểm của đường thẳng và đường tròn . Tính độ dài của dây .

Câu 3: Cho bốn điểm , , thẳng hàng như trong hình. Giả sử đường thẳng đi qua và vuông góc với đường thẳng thẳng .

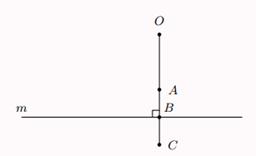
BÀI 16: VỊ TRÍ TƯƠNG ĐỐI CỦA ĐƯỜNG THẲNG VÀ ĐƯỜNG TRÒN

Cho các khẳng định sau:

i) Đường thẳng và đường tròn cắt nhau.

ii) Đường thẳng và đường tròn tiếp xúc nhau.

iii) Đường thẳng và đường tròn cắt nhau.

iv) Đường thẳng và đường tròn cắt nhau.

Số khẳng định đúng là:

Câu 4: Cho tam giác có và . Vẽ đường tròn tâm tiếp xúc với tại . Qua vẽ tia vuông góc với cắt tại điểm thứ hai (). Tính góc

Câu 5: Cho đường kính . Vẽ dây sao cho , trên tia đối của tia lấy điểm sao cho . Khi đó . Tính

Câu 6:Cho tam giác vuông tại , có . Vẽ đường cao . Gọi là điểm đối xứng với qua . Vẽ đường tròn đường kính cắt ở . Tính (đơn vị: cm) (Làm tròn kết quả đến hàng phần mười)

17,1

Câu 7: Cho tam giác ABC vuông tại A, có đường cao AH. Cho các phát biểu sau:

i) BC tiếp xúc với đường tròn .

ii) Gọi M và N là các điểm đối xứng với H lần lượt qua AB và AC. Khi đó BM và CN là hai tiếp tuyến của (A).

iii) .

iv) Cho HB = 2 cm và HC = 4,5 cm. Diện tích tứ giác BMNC là

Số câu phát biểu sai là:

Câu 8: Cho hai đường tròn đồng tâm và (). Từ điểm nằm ngoài , ta vẽ là tiếp tuyến của , là tiếp tuyến của (với là các tiếp điểm). Đường trung trực của đoạn cắt tại . Tính tỉ số .

BÀI TẬP THAM KHẢO THÊM

Câu hỏi 1: Cho AM và AN là hai tiếp tuyến cắt nhau của đường tròn (O), trong đó M và N là hai tiếp điểm. Gọi E là một điểm thuộc cung nhỏ MN. Tiếp tuyến của (O) tại E cắt AM tại B và cắt AN tại C. Biết AB = 10 cm, AC = 7 cm và BC = 6 cm. Tính độ dài của các đoạn thẳng AM, AN, BM và CN.

Trả lời: AM = AN = 11,5 cm, BM = 1,5 cm và CN = 4,5 cm.

Câu hỏi 2: Cho đường tròn (O) và điểm M nằm bên ngoài (O). Từ M kẻ tiếp tuyến MA với (O), trong đó A là tiếp điểm. Đường thẳng qua A và vuông góc với MO cắt (O) tại B (khác A).Tính OM và diện tích phần của tam giác AMB nằm bên ngoài (O), biết bán kính của (O) bằng 3 cm và góc MAB= 60°.

Trả lời: 9−3πcm².

Câu hỏi 3: Cho đường thẳng a, điểm M thuộc a và số dương R. Vẽ đường thẳng b đi qua M và vuông góc với a. Trên b xác định điểm A sao cho AM = R (đvđd). đường tròn (A; R) tiếp xúc với a tại M. Ta có thể vẽ được mấy đường tròn như thế?

Trả lời: hai

Câu hỏi 4: Cho đường thẳng và điểm cách một khoảng bằng . Không vẽ hình, hãy xét vị trí tương đối của đường thẳng và đường tròn

Trả lời:đường tròn không cắt đường thẳng

Câu hỏi 5: Cho đường thẳng và một điểm cách một khoảng . Xác định vị trí tương đối của với các đường tròn

Trả lời: không giao nhau

Câu hỏi 6: Cho đường tròn và đường thẳng . Gọi là chân đường vuông góc vẽ từ xuống , là độ dài của đoạn thẳng . Xác định vị trí tương đối của đường thẳng và đường tròn trong mỗi trường hợp

Trả lời: .............................................

Câu hỏi 7: Trong hệ tọa độ cho điểm . Hãy xác định vị trí tương đối của đường tròn tâm , bán kính với các trục Ox

Trả lời: .............................................

Câu hỏi 8: Cho đường thẳng và một điểm cách một khoảng . Vẽ đường tròn tâm , bán kính . Gọi và là các giao điểm của đường thẳng và đường tròn . Tính độ dài của dây .