Câu hỏi và bài tập tự luận toán 9 kết nối tri thức
Dưới đây là loạt câu hỏi và bài tập tự luận toán 9 kết nối tri thức. Bài tập tự luận chia 4 mức độ khác nhau: nhận biết, thông hiểu, vận dụng, vận dụng cao theo từng bài học sẽ hữu ích trong việc ôn tập, kiểm tra bài cũ, phiếu học tập, đề thi, kiểm tra...File tải về bản word, có đáp án và đầy đủ bài tập tự luận của các bài học. Kéo xuống để tham khảo.
Một số tài liệu quan tâm khác
Phần trình bày nội dung giáo án
BÀI 1: PHƯƠNG TRÌNH VÀ HỆ HAI PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
(20 câu)
1. NHẬN BIẾT (5 câu)
Câu 1: Phương trình nào sau đây là phương trình bậc nhất hai ẩn? Vì sao?
a) b)
c) d)
Trả lời:
Phương trình a), b), c) là phương trình bậc nhất hai ẩn vì các phương trình thỏa mãn điều kiện hoặc .
Phương trình d) không phải là phương trình bậc nhất hai ẩn vì hệ số .
Câu 2: Trong các cặp số cặp số nào là nghiệm của phương trình bậc nhất hai ẩn .
Trả lời:
+) Thay +) Thay và vào phương trình, ta có:
Vậy là nghiệm của phương trình đã cho.
+) Thay +) Thay và vào phương trình, ta có:
Vậy không là nghiệm của phương trình đã cho.
+) Thay +) Thay và vào phương trình, ta có:
Vậy là nghiệm của phương trình đã cho.
+) Thay +) Thay và vào phương trình, ta có:
Vậy không là nghiệm của phương trình đã cho.
Câu 3: Cặp số là nghiệm của phương trình nào trong các phương trình sau:
| a) | b) | c) |
| d) | e) | g) |
Trả lời:
a) Thay và vào phương trình, ta có: .
Vậy không là nghiệm của phương trình đã cho.
b) Thay và vào phương trình, ta có: .
Vậy là nghiệm của phương trình đã cho.
c) Thay và vào phương trình, ta có: .
Vậy không là nghiệm của phương trình đã cho.
d) Thay và vào phương trình, ta có: .
Vậy là nghiệm của phương trình đã cho.
e) Thay và vào phương trình, ta có: .
Vậy không là nghiệm của phương trình đã cho.
f) Thay và vào phương trình, ta có: .
Vậy không là nghiệm của phương trình đã cho.
Câu 4: Giả sử là nghiệm của phương trình bậc nhất hai ẩn .
Hoàn thành bảng sau đây:
| 0 | |||||
Từ đó suy ra 5 nghiệm của phương trình đã cho.
Trả lời:
Ta có:
| 0 | |||||
Vậy 5 nghiệm của phương trình đã cho là: , , ; ; .
Câu 5:
a) Hệ phương trình có là một hệ hai phương trình bậc nhất hai ẩn không? Vì sao?
b) Cặp số có là một nghiệm của hệ phương trình đó hay không? Vì sao?
Trả lời:
a) Hệ phương trình đã cho là một hệ phương trình bậc nhất hai ẩn vì hệ số của khác 0 và hệ số của khác 0.
b) Thay và vào từng phương trình ta có:
- - nên là nghiệm của phương trình thứ nhất;
- - nên không là nghiệm của phương trình thứ hai.
Vậy không là nghiệm của hệ phương trình đó.
2. THÔNG HIỂU (6 câu)
Câu 1: Tìm các giá trị của tham số để cặp số là nghiệm của phương trình .
Trả lời:
Vì là nghiệm của phương trình đã cho, ta có:
Vậy thì là nghiệm của phương trình đã cho.
Câu 2: Tìm trong mỗi trường hợp sau:
a) là nghiệm của phương trình ;
b) Điểm thuộc đường thẳng .
Trả lời:
a) Thay vào phương trình, ta có:
Vậy .
b) Thay vào đường thẳng, ta có:
Vậy .
Câu 3: Tìm nghiệm tổng quát của các phương trình sau:
a) b)
c) d)
Trả lời:
a)
Vậy phương trình có nghiệm tổng quát là
b)
Vậy phương trình có nghiệm tổng quát là
c)
Vậy phương trình có nghiệm tổng quát là
d)
Vậy phương trình có nghiệm tổng quát là
Câu 4: Cho phương trình .
1. Với , xét xem các cặp số sau, cặp số nào là nghiệm của phương trình.
a) b) ; c) .
2. Tìm nghiệm tổng quát của phương trình trên ứng với
a) ; b) .
3. Tìm giá trị tương ứng khi phương trình nhận các cặp số sau làm nghiệm.
a) b) .
Trả lời:
1. Với , ta có phương trình .
a) Thay vào phương trình, ta có:
Vậy không là nghiệm của phương trình.
b) Thay vào phương trình, ta có:
Vậy là nghiệm của phương trình.
c) Thay vào phương trình, ta có:
Vậy không là nghiệm của phương trình.
2.
a) Với ta có:
Vậy phương trình có nghiệm tổng quát là
b) Với ta có:
Vậy phương trình có nghiệm tổng quát là
3.
a) Thay vào phương trình, ta có:
b) Thay vào phương trình, ta có:
Câu 5: Cho hai phương trình đường thẳng:
và
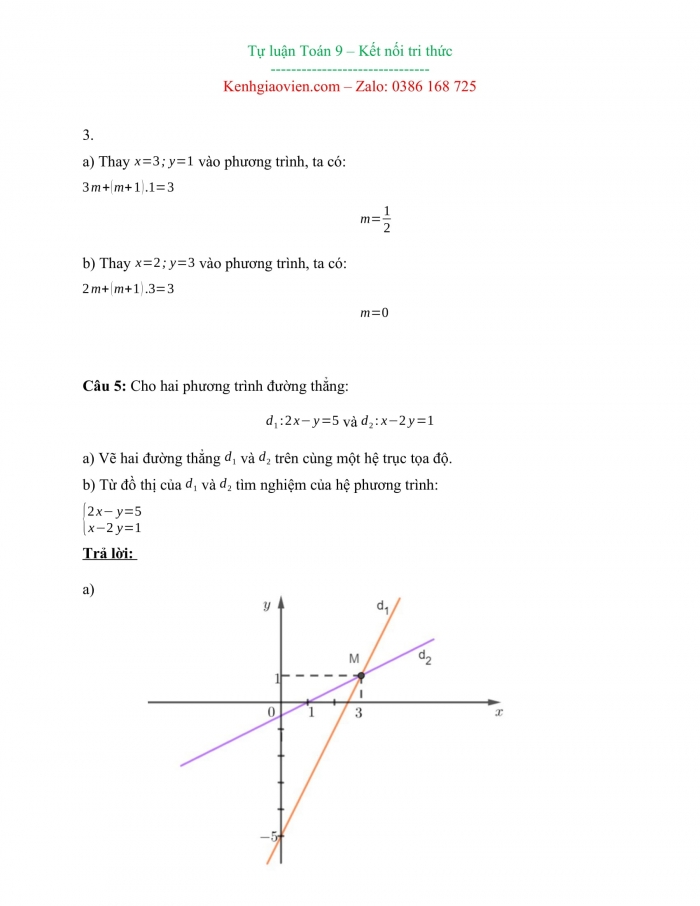
a) Vẽ hai đường thẳng và trên cùng một hệ trục tọa độ.
b) Từ đồ thị của và tìm nghiệm của hệ phương trình:
Trả lời:
a)
b) Ta thấy điểm vừa thuộc đường thẳng , vừa thuộc đường thẳng .
Vậy là nghiệm của hệ phương trình đã cho.
Câu 6: Hãy kiểm tra xem mỗi cặp số sau có là nghiệm của hệ phương trình tương ứng không:
a) và b) và
Trả lời:
a) Thay vào từng phương trình ta có:
+) +) nên không là nghiệm của phương trình thứ nhất.
+) +) nên không là nghiệm của phương trình thứ hai.
Vậy không là nghiệm của hệ phương trình đã cho.
b) Thay vào từng phương trình ta có:
+) +) nên là nghiệm của phương trình thứ nhất.
+) +) nên là nghiệm của phương trình thứ hai.
Vậy là nghiệm của hệ phương trình đã cho.
3. VẬN DỤNG (7 câu)
Câu 1: Cho biết và là hai nghiệm của phương trình bậc nhất hai ẩn. Hãy tìm phương trình bậc nhất hai ẩn đó.
Trả lời:
Gọi phương trình cần tìm có dạng:
Thay và vào phương trình ta được:
Chọn
Vậy phương trình cần tìm là: .
Chú ý:
- Nếu chọn (Loại)
- Nếu chọn , ta có thể chọn tùy ý. Tuy nhiên, nên cân nhắc chọn hợp lý để tìm được là những số “đẹp”.
Câu 2: Cho đường thẳng có phương trình
Tìm các giá trị của tham số để:
a) song song với trục hoành;
b) đi qua gốc tọa độ.
c) đi qua điểm .
Trả lời:
a) Để đường thẳng song song với thì:
b) Để đường thẳng đi qua gốc tọa độ ta thay vào phương trình:
c) Để đường thẳng đi qua ta thay vào phương trình:
Câu 3: Cho hệ phương trình . Tìm các giá trị của tham số để cặp số là nghiệm của phương trình đã cho.
Trả lời:
Thay vào từng phương trình ta có:
Vậy .
Câu 4: Cho các cặp số và hai phương trình
Trong các cặp số đã cho:
a) Những cặp số nào là nghiệm của phương trình (1)?
b) Cặp số nào là nghiệm của hệ hai phương trình gồm (1) và (2)?
c) Vẽ hai đường thẳng và trên cùng một mặt phẳng tọa độ để minh họa kết luận ở câu b.
Trả lời:
a) Thay vào phương trình (1) ta có: .
Vậy không là nghiệm của phương trình (1).
+) +) Thay vào phương trình (1) ta có: .
Vậy không là nghiệm của phương trình (1).
+) +) Thay vào phương trình (1) ta có: .
Vậy là nghiệm của phương trình (1).
+) +) Thay vào phương trình (1) ta có: .
Vậy là nghiệm của phương trình (1).
b) Thay vào phương trình (2) ta có: .
Vậy là nghiệm của phương trình (2).
Mà cũng là nghiệm của phương trình (1).
Vậy là nghiệm của hệ hai phương trình gồm (1) và (2).
c)
Câu 5: Viết công thức nghiệm tổng quát và biểu diễn tập nghiệm của các phương trình sau trên mặt phẳng tọa độ:
| a) | b) | c) |
Trả lời:
a)
Vậy phương trình có nghiệm tổng quát là
b)
Vậy phương trình có nghiệm tổng quát là
c)
Vậy phương trình có nghiệm tổng quát là
Câu 6: Cho hệ phương trình . Tìm để hệ:
a) Có nghiệm duy nhất; b) Vô nghiệm;
c) Vô số nghiệm.
Trả lời:
a) Hệ có nghiệm duy nhất khi:
b) Hệ vô nghiệm khi:
c) Hệ có vô số nghiệm khi
Câu 7: Năm bạn Hoa, Hà, Minh, Trung, Mạnh cùng đi mua sticker để trang trí vở. Có hai loại sticker: loại I giá 3 nghìn đồng/chiếc và loại II giá 4 nghìn đồng/chiếc. Mỗi bạn mua 2 chiếc và tổng số tiền năm bạn phải trả là 14 nghìn đồng. Gọi lần lượt là số sticker loại I và loại II mà năm bạn đã mua.
a) Viết hệ phương trình bậc nhất hai ẩn .
b) Cặp số có phải là nghiệm của hệ phương trình ở câu a hay không? Vì sao?
Trả lời:
a) Theo đề bài, ta có:
b) Thay vào từng hệ phương trình, ta có:
Vậy không phải là nghiệm của hệ phương trình trên.
4. VẬN DỤNG CAO (2 câu)
Câu 1: Cho phương trình .
a) Tìm tất cả các nghiệm nguyên của phương trình.
b) Tìm tất cả các nghiệm nguyên dương của phương trình.
Trả lời:
a) Nhẩm nghiệm, ta có là một nghiệm của nên ta có:
b) Vì nguyên dương nên ta có:
Câu 2: Cho ba đường thẳng:
và
Tìm các giá trị của tham số để ba đường thẳng và đồng quy.
Trả lời:
Ta có đồ thị hàm số của hai đường thẳng và là:
Từ đồ thị hàm số ta nhận thấy điểm thuộc cả hai đường thẳng.
Vậy để và đồng quy thì .
Thay vào phương trình ta có:
Vậy thì ba đường thẳng và đồng quy.
MỘT VÀI THÔNG TIN
- Trắc nghiệm tải về là bản word
- Các câu tự luận có nhiều mức độ, có đáp án
- Đã có đủ kì I, đang cập nhật liên tục để đến 30/12 có đủ cả năm
PHÍ TÀI LIỆU:
- 150k/học kì - 200k/cả năm
CÁCH TẢI:
- Bước 1: gửi phí vào tk: 10711017 - Chu Văn Trí - Ngân hàng ACB (QR)
- Bước 2: Nhắn tin tới Zalo Fidutech - nhấn vào đây thông báo và nhận tài liệu
=> Giáo án toán 9 kết nối tri thức
Tài liệu được tặng thêm:
Từ khóa: Câu hỏi và bài tập tự luận toán 9 kết nối tri thức, bài tập toán 9 KNTT, bộ câu hỏi tự luận toán 9 kết nối tri thức