Giáo án powerpoint dạy thêm Toán 8 kết nối Bài tập cuối chương 4

THÂN MẾN CHÀO CÁC EM HỌC SINH ĐẾN VỚI BÀI HỌC MỚI 

BÀI TẬP CUỐI CHƯƠNG IV 

PHIẾU BÀI TẬP SỐ 1 

Bài 1. Cho tam giác ABC. Gọi Bx và Cy lần lượt là các đường chứa tia phân giác của các góc ngoài tại đỉnh B và C. Gọi H và K lần lượt là hình chiếu của A trên Bx và Cy 

1. a) Chứng minh tứ giác BCKH là hình thang.
2. b) Tam giác ABC phải có điều kiện gì để hình thang BCKH là hình thang cân.

Giải 

1. a) Gọi D và E lần lượt là giao điểm của AH và AK với đường thẳng BC

∆ABD có BH vừa là phân giác, vừa là đường cao nên là tam giác cân  

=> HA = HD 

Tương tự, ta có: KA = KE 

Xét ∆ADE có HK là đường trung bình nên HK // DE => HK // BC 

Vậy tứ giác BCKH là hình thang. 

1. b) Ta có : (H_1 ) ̂=(B_1 ) ̂;(K_1 ) ̂=(C_1 ) ̂ (slt)

Hình thang BCKH là hình thang cân =>(H_1 ) ̂=(K_1 ) ̂=>(B_1 ) ̂=(C_1 ) ̂ 

=>(ABD) ̂=(ACE) ̂=>(ABC) ̂=(ACB) ̂=>∆ABC cân tại A 

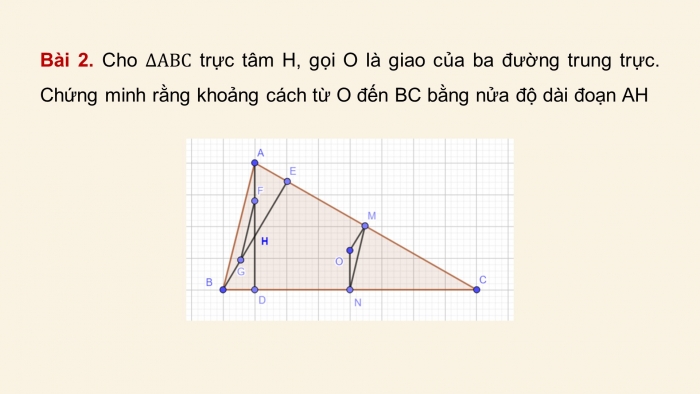
Bài 2. Cho ∆ABC trực tâm H, gọi O là giao của ba đường trung trực. Chứng minh rằng khoảng cách từ O đến BC bằng nửa độ dài đoạn AH 

Giải 

Gọi M và N lần lượt là trung điểm của BC và CA. 

Gọi F và G lần lượt là trung điểm của AH và BH 

Ta có MN là đường trung bình của ∆ABC; FG là đường trung bình của ∆ABH 

=> MN // AB và MN=1/2 AB 

=> FG // AB và FG=1/2 AB 

Do đó: MN // FG và MN = FG 

Dễ thấy OM // AD và ON // BE 

Xét ∆OMN và ∆HFG có: 

+ MN=FG; 

+ (OMN) ̂=(HFG) ̂ 

+ (ONM) ̂=(HGF) ̂ (hai góc có cạnh tương ứng song song) 

Vậy ∆OMN=∆HFG (g.c.g)=>OM=HF=AH/2 

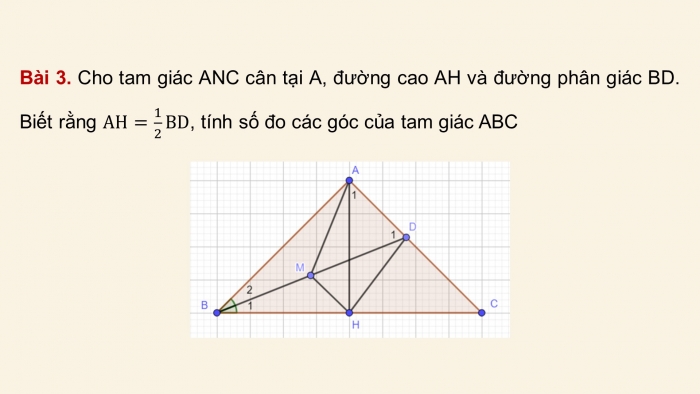
Bài 3. Cho tam giác ANC cân tại A, đường cao AH và đường phân giác BD. Biết rằng AH=1/2 BD, tính số đo các góc của tam giác ABC 

Giải 

Gọi M là trung điểm của BD thì: 

MD=1/2 BD=AH 

∆ABC cân tại A, AH là đường cao nên HB = HC 

Ta có HM là đường trung bình của ∆BCD => HM // AC 

Hình thang HMAD có hai đường chóe bằng nhau nên là hình thang cân. 

∆ADH=∆DAM (c.c.c)=>(A_1 ) ̂=(D_1 ) ̂⇔90°-C ̂=(B_1 ) ̂+C ̂ (1) 

Ta đặt: B ̂=C ̂=x thì (1) ⇔90°-x=x/2+x ⇔x=36° 

Vậy ∆ABC có B ̂=C ̂=36°;A ̂=108° 

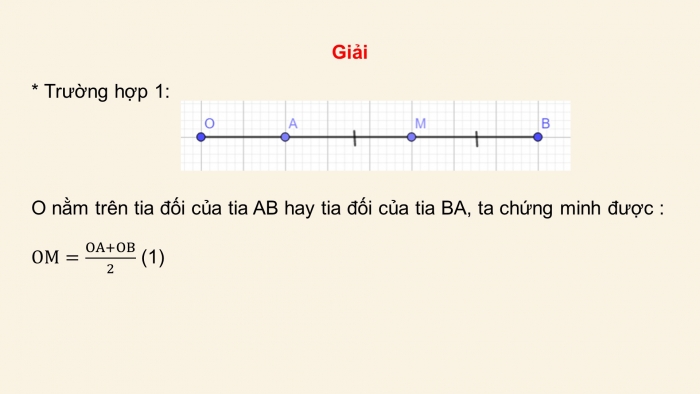
Bài 4. Cho đoạn thẳng AB và n điểm O_1, O_2,…, O_n không nằm giữa A và B sao cho O_1 A+O_2 A+…+O_n A=O_1 B+O_2 B+…+O_n B=a.  

Chứng minh rằng tồn tại một điểm M sao cho O_1 M+O_2 M+…+O_n M≤a 

Giải 

* Trường hợp 1: 

O nằm trên tia đối của tia AB hay tia đối của tia BA, ta chứng minh được : 

OM=(OA+OB)/2 (1) 

* Trường hợp 2: 

Trường hợp O không thẳng hàng với A và B 

Gọi N là trung điểm của OB, khi đó MN là đường trung bình của ∆OAB 

MN=OA/2  

Xét ∆OMN, ta có: OM < MN + ON 

=>OM<(OA+OB)/2 (2) 

Từ (1)(2) suy ra: OM≤(OA+OB)/2 (*) 

Áp dụng hệ thức (*) với n điểm O_1, O_2,…, O_n ta có: 

O_1 M≤(O_1 A+O_1 B)/2;O_2 M≤(O_2 A+O_2 B)/2;…;O_n M≤(O_n A+O_n B)/2  

Cộng trừ các vế bất đẳng thức ta có: 

O_1 M+O_2 M+…+O_n M≤(O_1 A+O_1 B)/2+(O_2 A+O_2 B)/2+…+(O_n A+O_n B)/2  

=(O_1 A+O_2 A+…+O_n A)/2+(O_1 B+O_2 B+…+O_n B)/2=a/2+a/2=a 

PHIẾU BÀI TẬP SỐ 2 

Bài 1. Cho tam giác ABC, các trung tuyến AD, BE, CF cắt nhau tại G. 

1. a) Tính AE/AC
2. b) Tính AG/GD
3. c) Kể hai cặp đoạn thẳng tỉ lệ với AG và GD

Giải 

1. a) Có E là trung điểm của AC (vì BE là trung tuyến)

=> AE/AC=1/2 (tính chất trung điểm của đoạn thẳng) 

1. b) ∆ABC có các trung tuyến AD, BE, CF cắt nhau tại G

=>G là trọng tâm ∆ABC 

=>AG/GD=2/1=2  

1. c) G là trong tâm ∆ABC=>AG/GD=BG/GE=CG/GF

=> BG và GE là cặp đoạn thẳng tỉ lệ với AG và GD 

=> CG và GH là cặp đoạn thẳng tỉ lệ với AG và GD 

Bài 2. Cho góc xOy. Trên tia Ox lấy theo thứ tự hai điểm A và B sao cho  

OA = 2cm; AB = 3cm. Trên tia Oy lấy C với OC = 3cm.  

Từ B kẻ đường thẳng song song với AC cắt Oy tại D. Tính độ dài CD? 

Giải 

Xét ∆OBD có: AC // BD (gt) 

=> AO/AB=OC/CD (định lí Talet) 

=> CD=(AB.OC)/OA=3.3/2=4,5 cm 

Bài 3. Cho tam giác ABC có AM là trung tuyến và điểm E thuộc đoạn MC. Qua E kẻ đường thẳng song song với AC, cắt AB ở D và cắt AM ở K. Qua E kẻ đường thẳng song song với Ab cắt AC ở F. Chứng minh AF = DK. 

...