Giáo án powerpoint dạy thêm Toán 8 kết nối Bài 14: Hình thoi và hình vuông

VUI MỪNG CHÀO ĐÓN CÁC EM TỚI BUỔI HỌC NGÀY HÔM NAY

BÀI 14: HÌNH THOI VÀ HÌNH VUÔNG

PHIẾU BÀI TẬP SỐ 1

DẠNG 1: Chứng minh một tứ giác là hình thoi

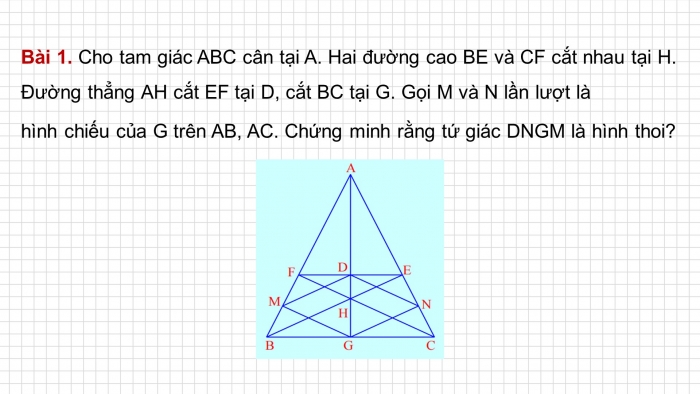
Bài 1. Cho tam giác ABC cân tại A. Hai đường cao BE và CF cắt nhau tại H. Đường thẳng AH cắt EF tại D, cắt BC tại G. Gọi M và N lần lượt là

hình chiếu của G trên AB, AC. Chứng minh rằng tứ giác DNGM là hình thoi?

Luyện tập

Ta có

Vì H là trực tâm của , đồng thời là đường

trung tuyến, từ đó ta có

Xét GN // BE (cùng vuông góc với AC) và GB = GC

Chứng minh tương tự ta có: MF = MB

Dễ dàng chứng minh được DM // Gn và DM = GN. Vậy tứ giác DNGM là hình bình hành.

Mặt khác, DM = DN nên DNGM là hình thoi.

Bài 2. Cho hình bình hành ABCD có AC vuông góc với AD. Gọi E, F theo thứ tự là trung điểm của cạnh AB và CD. CHứng minh AECF là hình thoi?

Lời giải

Xét tứ giác AECF có: AE // CF (gt) và AE = CF (gt) nên AECF là

hình bình hành

Vì E là trung điểm của AB và F là trung điểm của CD nên EF // AD // BC

Mà . Vậy hình bình hành AECF là hình thoi vì có

hai đường chéo vuông góc với nhau

Bài 3. Cho hình thoi ABCD có . Từ đỉnh góc B kẻ các đường

vuông góc BE và BF đến AD và DC, cắt AC theo thứ tự ở M và N.

Chứng minh:

a) AE = CF

b)  đều

c) Tứ giác BMND là hình thoi

Lời giải

a) Xét

+  +

+ AB = BC (ABCD là hình thoi) + AB = BC (ABCD là hình thoi)

+  +  (gt)

Vậy (g.c.g)

b) Ta có:

 (Tâm giác cân có 1 góc bằng 60)

Lời giải

c) Ta đi chứng minh MB = BN = ND = DM

+ AC là trung trực của BD  + AC là trung trực của BD  (1)

+ AC là trung trực của BD  + AC là trung trực của BD

+  +

Từ (1)(2)(3) ta có BMND là hình thoi

Bài 4. Cho tam giác ABC đều trong tâm G. Vẽ hình chữ nhật ABDE sao cho C thuộc đoạn thẳng DE. Tia AG cắt BD tại I, tia AE cắt BG tại J. Chứng minh:

a) I và J đối xứng nhau qua CG?

b) Các tứ giác:

CGBI, GICJ, CJAG là hình thoi?

Lời giải

a)    Ta có

 có hai đáy AI và BJ

Vì hình thân cân ABIJ có 1 góc vuông nên ABIJ là hình chữ nhật tâm G.

Mặt khác  là đường trung trực của cạnh IJ

Vậy I và J đối xứng nhau qua CG

Lời giải

b) Ta có

Gọi M là trung điểm của BC, trong tam giác BGI có BM là đường cao,

đường phân giác nên M là trung điểm của GI.

Tứ giác CBDI có hai đường chéo BC và GI vuông góc với nhau và cắt nhau ở trung điểm mỗi đường, do đó: CBGI là hình thoi.

Chứng minh tương tự ta có CBGI là hình thoi.

Vì I và J đối xứng nhau qua đường thẳng CG nên CI = CJ, GI = GJ (1)

Dễ thấy là tam giác đều  (2)

Từ (1)(2) suy ra GICJ có 4 cạnh bằng nhau nên là hình thoi.

PHIẾU BÀI TẬP SỐ 2

DẠNG 2: Vận dụng tính chất của hình thoi để chứng minh quan hệ bằng nhau, song song, vuông góc, đồng quy, tính độ dài các đoạn thẳng

Bài 1. Cho hình thoi ABCD, có góc B bằng 60 Kẻ . Chứng minh AE = AF

Lời giải

Do AC là phân giác góc , xét  và

+  +

+ AC chung + AC chung

+  +

Vậy  (g.c.g) => AE = AF