Giáo án và PPT đồng bộ Toán 10 chân trời sáng tạo
Toán 10 chân trời sáng tạo. Giáo án word chỉn chu. Giáo án ppt (powerpoint) hấp dẫn, hiện đại. Word và PPT được soạn đồng bộ, thống nhất với nhau. Bộ tài liệu sẽ giúp giáo viên nhẹ nhàng trong giảng dạy. Thầy/cô tham khảo trước để biết chất lượng.
Click vào ảnh dưới đây để xem giáo án rõ
























Một số tài liệu quan tâm khác
Phần trình bày nội dung giáo án
Trường:…………..
Giáo viên:
Bộ môn: Toán 10 Chân trời sáng tạo
PHẦN 1: SOẠN GIÁO ÁN WORD TOÁN 10 CHÂN TRỜI SÁNG TẠO
BÀI 2: TẬP HỢP
I. MỤC TIÊU:
1. Kiến thức, kĩ năng: Học xong bài này, HS đạt các yêu cầu sau:
- Nhận biết và thể hiện được các khái niệm tập hợp, phần tử, quan hệ liên thuộc, tập rỗng; sử dụng kí hiệu
 ; viết được tập hợp dưới dạng liệt kê các phần tử và dưới dạng chỉ ra tính chất đặc trưng cho các phần tử.
; viết được tập hợp dưới dạng liệt kê các phần tử và dưới dạng chỉ ra tính chất đặc trưng cho các phần tử. - Nhận biết và thể hiện được quan hệ bao hàm giữa các tập hợp, khái niệm tập con, hai tập hợp bằng nhau, sử dụng đúng các kí hiệu
 ,
, 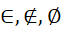 ,...), ... để biểu đạt, tiếp nhận (viết và nói) các ý tưởng, thông tin một cách rõ ràng, súc tích và chính xác.
,...), ... để biểu đạt, tiếp nhận (viết và nói) các ý tưởng, thông tin một cách rõ ràng, súc tích và chính xác. - Sử dụng được biểu đồ Ven để biểu diễn tập hợp, quan hệ bao hàm giữa các tập hợp.
2. Năng lực
- Năng lực chung:
Năng lực tự chủ và tự học trong tìm tòi khám phá
Năng lực giao tiếp và hợp tác trong trình bày, thảo luận và làm việc nhóm
Năng lực giải quyết vấn đề và sáng tạo trong thực hành, vận dụng.
Năng lực riêng:
Năng lực giao tiếp toán học: HS sử dụng các khái niệm, thuật ngữ (tập hợp, phần tử, tập rỗng, thuộc, tập con, nằm trong, hợp, giao, ...), các sơ đồ, biểu đồ (biểu đồ Ven), kí hiệu
 để biểu đạt, tiếp nhận (viết và nói) các ý tưởng, thông tin (trong học tập cũng như trong đời thường) một cách rõ ràng, súc tích và chính xác.
để biểu đạt, tiếp nhận (viết và nói) các ý tưởng, thông tin (trong học tập cũng như trong đời thường) một cách rõ ràng, súc tích và chính xác.
3. Phẩm chất
Có ý thức học tập, ý thức tìm tòi, khám phá và sáng tạo, có ý thức làm việc nhóm, tôn trọng ý kiến các thành viên khi hợp tác.
- Chăm chỉ tích cực xây dựng bài, có trách nhiệm, chủ động chiếm lĩnh kiến thức theo sự hướng dẫn của GV.
II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU
1. Đối với GV: SGK, Tài liệu giảng dạy, giáo án, đồ dùng dạy học, thước thẳng có chia khoảng, phiếu học tập.
2. Đối với HS: SGK, SBT, vở ghi, giấy nháp, đồ dùng học tập (bút, thước...), bảng nhóm, bút viết bảng nhóm.
III. TIẾN TRÌNH DẠY HỌC
A. HOẠT ĐỘNG KHỞI ĐỘNG (MỞ ĐẦU)
a) Mục tiêu:
- Thông qua tình huống thực tế gần gũi liên quan đến phân loại các đối tượng thành các nhóm, nhóm con, khơi gợi ý tưởng hình thành khái niệm tập hợp và tập hợp con.
b) Nội dung: HS thực hiện yêu cầu của hoạt động, trình bày được phương án của mình.
c) Sản phẩm: HS trả lời được câu hỏi mở đầu, bước đầu có hình dung về tập hợp, phần tử thuộc tập hợp, tập con.
d) Tổ chức thực hiện:
Bước 1: Chuyển giao nhiệm vụ:
- GV yêu cầu HS đọc tình huống mở đầu:

- GV nhắc lại: Ở lớp 6, chúng ta đã dùng từ tập hợp để gọi một nhóm đối tượng hoàn toàn xác định nào đó, mỗi đối tượng của nhóm gọi là một phần tử của tập hợp đó.
+ Hãy chỉ ra các tập hợp và phần tử của tập hợp sách mà em vừa phân chia.
Bước 2: Thực hiện nhiệm vụ: HS quan sát và chú ý lắng nghe,
Bước 3: Báo cáo, thảo luận: GV gọi một số HS trả lời, HS khác nhận xét, bổ sung.
Bước 4: Kết luận, nhận định: GV đánh giá kết quả của HS, trên cơ sở đó dẫn dắt HS vào bài học mới: "Phần tử của tập hợp sách em vừa nêu có thể cũng là phần tử của một tập hợp khác, khi đó có mối quan hệ gì giữa các tập hợp này. Hay các nhóm sách trước phân chia và nhóm sách sau phân chia có mối quan hệ như thế nào trong tập hợp, hôm nay chúng ta cùng đi tìm hiểu để hiểu rõ hơn".
B. HÌNH THÀNH KIẾN THỨC MỚI
Hoạt động 1: Nhắc lại về tập hợp
a) Mục tiêu:
- Nhận biết và thể hiện được khái niệm tập hợp, phần tử, sử dụng các kí hiệu ![]() , kí hiệu số phần tử.
, kí hiệu số phần tử.
- Phát biểu được thế nào là tập rỗng.
- Viết tập hợp dưới các dạng khác nhau.
b) Nội dung:
HS đọc SGK, nghe giảng, suy nghĩ trả lời câu hỏi, đọc hiểu các Ví dụ 1, 2, 3, thực hiên hoạt động Thực hành 1, 2, 3.
c) Sản phẩm: HS hình thành được kiến thức bài học, lấy các ví dụ về tập hợp, xác định phần tử thuộc hay không thuộc, viết tập hợp dưới dạng liệt kê hoặc chỉ ra tính chất đặc trưng.
-----------Còn tiếp-----------
PHẦN 2: BÀI GIẢNG POWERPOINT TOÁN 10 CHÂN TRỜI SÁNG TẠO
CHƯƠNG III: HÀM SỐ BẬC HAI VÀ ĐỒ THỊ
BÀI 3: HÀM SỐ VÀ ĐỒ THỊ
Tiết 1: HÀM SỐ. TẬP XÁC ĐỊNH VÀ TẬP GIÁ TRỊ CỦA HÀM SỐ
KHỞI ĐỘNG
Quan sát bảng nhiệt độ bên dưới. Hãy cho nhiệt độ có mối liên hệ gì với thời gian. Em có thể mô tả sự phụ thuộc của nhiệt độ vào thời gian không?
NỘI DUNG
HD1: Nhận biết hàm số cho bằng bảng và biểu đồ
Quan sát bản tin dự báo thời tiết tại TP. Hồ Chí Minh được ghi lại trong bảng và hình bên:
Thảo luận nhóm ba và trả lời các câu hỏi:
- a) Viết tập hợp các mốc giờ đã có dự báo nhiệt độ.
- b) Viết tập hợp các số đo nhiệt độ đã dự báo.
- c) Cho biết nhiệt độ dự báo tại TP.Hồ Chí Minh vào lúc 7 giờ sáng ngày 01/5/2021.
TL:
- a) Tập hợp các mốc giờ đã có dự báo nhiệt độ là :
A = {1; 4; 7; 10; 13; 16; 19; 22}
- b) Tập hợp các số đo nhiệt độ đã dự báo là:
B = {28; 27; 32; 31; 29; 28; 27}
- c) Nhiệt độ dự báo tại TP. Hồ Chí Minh vào lúc 7 giờ sáng ngày 01/5/2021 là: 28⁰C.
HĐ2
Nhận biết hàm số cho bằng công thức - Khái niệm hàm số
Giả sử x và y là hai đại lượng biến thiên và x nhận giá trị thuộc tập số D.
Nếu với mỗi giá trị của x thuộc tập hợp số D có một và chỉ một giá trị tương ứng của y thuộc tập hợp số thực R thì ta có một hàm số.
Ta gọi x là biến số và y là hàm số của x.
Tập hợp D gọi là tập xác định của hàm số.
Tập hợp T gồm tất cả các giá trị y (tương ứng với x thuộc D) gọi là tập giá trị của hàm số.
Ta thường dùng kí hiệu f(x) để chỉ giá trị y tương ứng với x, nên hàm số còn được viết là y = f(x)
VD: y = 3x + 5; y = - 2
Nhận xét:
Một hàm số có thể được cho bằng bảng, bằng biểu đồ, hoặc bằng công thức.
Ví dụ 1
- Vì sao có thể nói bảng dữ liệu dự báo thời tiết (Bảng 1) biểu thị một hàm số? Tìm tập xác định và tập giá trị của hàm số này.
- Biểu đồ “Dự báo thời tiết ngày 1/5/2021 tại TP. HCM (Hình 1) có biểu thị hàm số không? Tại sao?
Giải
- a) Bảng dữ liệu dự báo thời tiết (Bảng 1) biểu thị một hàm số vì: ứng với mỗi thời điểm (giờ) trong bảng đều có một giá trị dự báo nhiệt độ duy nhất.
Tập xác định của hàm số:
D = {1; 4; 7; 10; 13; 16; 19; 22}
Tập giá trị của hàm số:
T = {27; 28; 29; 31; 32}
- b) Biểu đồ “Dự báo nhiệt độ ngày 01/5/2021 tại Thành phố Hồ Chí Minh” biểu thị một hàm số vì: ứng với mỗi thời điểm (giờ) trong biểu đồ đều có một giá trị dự báo nhiệt độ duy nhất.
TXĐ và tập giá trị của hàm số như câu a.
Chú ý:
- a) Khi một hàm số được cho bằng công thức mà không chỉ rõ tập xác định thì ta quy ước:
Tập xác định của hàm số y = f(x) là tập hợp tất cả các số thực x sao cho biểu thức f(x) có nghĩa.
- b) Một hàm số có thể được cho bởi hay hay nhiều công thức. Chẳng hạn, xét hàm số:
nghĩa là với x 1 thì f(x) = -3x + 5; với x > 1 thì f(x) = 2
Ví dụ 2
Tìm tập xác định của các hàm số sau:
- f(x) =
- f(x) =
- a) Biểu thức f(x) có nghĩa => 5 - x ≥ 0 ó x ≤ 5
- Vậy TXĐ của hàm số:
- D = (-∞; 5]
- b) Biểu thức f(x) có nghĩa => 2x - 6 ≠ 0 ó x ≠ 3
- Vậy TXĐ của hàm số:
- D = R \ {3}
HD3: Thực hành
Chia lớp thành 4 nhóm và thực hiện các nhiệm vụ:
- Nhóm 1 + 3: Thực hiện Thực hành 1
- Nhóm 2 + 4: Thực hiện Thực hành 2
Thực hành 1:
Một thiết bị đã ghi lại vận tốc v (mét/ giây) ở thời điểm t (giây) của một vật chuyển động như trong bảng sau:
| t | 0,5 | 1 | 1,2 | 1,8 | 2,5 |
| v | 1,5 | 3 | 0 | 5,4 | 7,5 |
Vì sao bảng này biểu thị một hàm số? Tìm TXĐ của hàm số này.
Giải
Bảng đó biểu thị một hàm số vì:
Ứng với mỗi thời điểm t có duy nhất một giá trị v.
Tập xác định của hàm số:
D = {0,5; 1; 1,2; 1,8; 2,5}
Thực hành 2:
Tìm tập xác định của các hàm số sau:
- a) f(x) =
Biểu thức f(x) có nghĩa ó 2x + 7 ≥ 0 ó x ≥
Vậy TXĐ của hàm số: D = [ ; + ∞)
- b) f(x) =
Biểu thức f(x) có nghĩa
- 3x + 2 ≠ 0 ó (x - 1)(x - 2) ≠ 0
Vậy TXĐ của hàm số: D = R \ {1; 2}
LUYỆN TẬP
Bài 1 (SGK - tr48)
Xác định tập xác định của các hàm số sau:
- a) f(x) =
- b) f(x) = 2 +
TL:
- a) Biểu thức f(x) có nghĩa => -5x + 3 ≥ 0 => x ≤
Vậy TXĐ của hàm số D = (-∞;
- b) Biểu thức f(x) có nghĩa => x + 3 ≠ 0 ó x ≠ -3
Vậy TXĐ của hàm số D = R \ {-3}
Bài 6 (SGK - tr.48)
Giải
a)
- i) Hàm số để tính số tiền hành khách phải trả khi di chuyển x (km) bằng xe taxi 4 chỗ là :
- ii) Hàm số để tính số tiền hành khách phải trả khi di chuyển x (km) bằng xe taxi 7 chỗ là :
- b) Có : 30 = 4.7 + 2
=> Nếu cần đặt taxi cho 30 hành khách, sẽ cần ít nhất 8 xe 4 chỗ và 5 xe 7 chỗ.
Số tiền phải trả nếu thuê toàn bộ xe 4 chỗ là :
- [11 000 + 14 500. 31 + 11 600(x - 31)] = 807 500 + 92 800. x (1)
Số tiền phải trả nếu thuê toàn bộ xe 4 chỗ là :
- 5. [11 000 + 15 500. 31 + 13 600(x - 31)] = 349 500 + 68 000. x (2)
Từ (1) và (2) => đặt toàn bộ xe 7 chỗ sẽ có lợi hơn.
VẬN DỤNG
Bài tập (SGK – tr.43)
Ở góc của miếng đất hình chữ nhật, người ta làm một bồn hoa có dạng một phần tư hình tròn với bán kính r (Hình 2). Bán kính bồn hoa có kích thước từ 0,5 m đến 3 m.
- a) Viết công thức của hàm số biểu thị diện tích của bồn hoa theo r và tìm TXĐ của hàm số này.
- b) Bán kính bồn hoa bằng bao nhiêu thì nó có diện tích là 0,5
Giải
- a) Công thức của hàm số biểu thị diện tích bồn hoa theo bán kính r là :
Tập xác định của hàm số: D = [0,5 ; 3]
- f(x) = 0,5ó = 0,5 ó = 2
- r = (cm) (loại r = -vì không thỏa mãn D)
Vậy r = cm
TRÒ CHƠI: ĐƯỜNG LÊN ĐỈNH OLYMPIA
Câu hỏi: Tập xác định của hàm số y = là?
- D = R B. D = (1; +∞)
- D = R \{1} D. D = [1; +∞)
Câu hỏi: Tìm TXĐ của hàm số y = - ?
- D = [-3; +∞) B. D = [-2; +∞)
- D = R D. D = [2; +∞)
Câu hỏi: Biểu thức nào sau đây không phải là hàm số?
- y = x - 1 B. y =
- y = D. |y| = 5x
Câu hỏi: Tập giá trị của hàm số y = là?
- R B. (0; + ∞)
- (- ∞; 0) D. [0; +∞)
Câu hỏi: Tìm tất cả các giá trị thực của tham số m để hàm số y = xác định trên R
- m ≥ 11 B. m > 11
- m < 11 D. m ≤ 11
------Còn tiếp-----------
PHẦN 3: TÀI LIỆU THAM KHẢO ĐƯỢC TẶNG KÈM
1. TRỌN BỘ TRẮC NGHIỆM TOÁN 10 CHÂN TRỜI SÁNG TẠO
Bộ trắc nghiệm Toán 10 Chân trời sáng tạo tổng hợp câu hỏi trắc nghiệm: nhận biết, thông hiểu, vận dụng, vận dụng cao và trắc nghiệm Đ/S
ÔN TẬP CHƯƠNG 9. PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG
Câu 1: Đường thẳng đi qua điểm A(1; -2) và nhận (2; 4) làm vectơ pháp tuyến có phương trình là:
- x + 2y + 3 = 0
- x – 2y + 4 = 0
- x – 2y – 5 = 0
- 2x – 4y = 0
Câu 2: Đường tròn x2 + y2 – 5y = 0 có bán kính bằng bao nhiêu ?
- 25
Câu 3: Cho elip (E) có hai tiêu điểm là F1, F2 và có độ dài trục lớn là 2a. Trong các mệnh đề sau, mệnh đề nào đúng?
- 2a = F1F2
- 2a > F1F2
- 2a < F1F2
- 4a = F1F2
Câu 4: Phương trình nào là phương trình của đường tròn có tâm I(-3; 4) và bán kính R = 2?
- (x + 3)2+ (y – 4)2– 4 = 0
- (x – 3)2+ (y – 4)2= 4
- (x + 3)2+ (y – 4)2= 4
- (x + 3)2+ (y – 4)2= 2
Câu 5: Phương trình tổng quát của đường thẳng đi qua A(1; -2) và nhận (-1; 2) làm vectơ pháp tuyến có phương trình là:
- -x + 2y = 0
- x + 2y + 4 = 0
- x – 2y – 5 = 0
- x – 2y + 4 = 0
Câu 6: Cho ba vectơ = (1; 1), = (2; 2), = (-1; -1).
Tìm tọa độ của vectơ: + 2− 3
- (9; 26)
- (4; -9)
- (13; 27)
- (8; 8)
Câu 7: Cho hai điểm A(–2; 3) và B(4; –1). Phương trình đường trung trực của đoạn thẳng AB là:
- 2x – 3y + 1 = 0
- 2x + 3y – 5 = 0
- 3x – 2y – 1 = 0
- x – y – 1 = 0
Câu 8: Tọa độ tâm I và bán kính R của đường tròn có phương trình:
(x – 1)2 + (y – 10)2 = 81 lần lượt là
- I(1; 10) và R = 9
- I(–1; –10) và R = 9
- I(1; 10) và R = 81
- I(–1; –10) và R = 81
Câu 9: Cho elip (E): . Trong các khẳng định sau, khẳng định nào sai?
- (E) có các tiêu điểm F1(–4; 0) và F2(4; 0)
- (E) có tỉ số
- (E) có đỉnh A1(–5; 0)
- (E) có độ dài trục nhỏ bằng 3
Câu 10: Cho hai vectơ = (1; 2), = (3; 0). Tìm tọa độ của vectơ 2 + 3.
- (10; 5)
- (11; 4)
- (2; 3)
- (11; 6)
Câu 11: Cho điểm M(4; 5). Tìm tọa độ điểm M' đối xứng với M qua trục Ox
- (4; 0)
- (4; -5)
- (0; 5)
- (-4; 5)
Câu 12: Cho ∆ABC có A(2; –1), B(4; 5), C(–3; 2). Phương trình nào sau đây là phương trình tổng quát của đường cao AH?
- 7x + 3y – 11 = 0
- 3x + 7y + 1 = 0
- 7x + 3y + 13 = 0
- –3x + 7y + 13 = 0
Câu 13: Cho đường tròn (C): x2 + y2 + 5x + 7y – 3 = 0. Khoảng cách từ tâm của (C) đến trục hoành bằng:
- 5
- 7
Câu 14: Viết phương trình chính tắc của Elip có độ dài trục lớn và trục nhỏ lần lượt là 20 và 10.
Câu 15: Phương trình đường tròn tâm O(0; 0) bán kính R = 2 là
- (x– 1)2 + (y – 1)2 = 4
- (x– 1)2 – (y – 1)2 = 4
- x2+ y2 = 4
- x2– y2 = 4
Câu 16: Đường thẳng d có một vectơ chỉ phương là = (3; −4). Đường thẳng ∆ vuông góc với d có một vectơ pháp tuyến là:
- = (4; 3)
- = (−4; −3)
- = (3; 4)
- = (3; −4)
Câu 17: Cho điểm M(4; 5). Tìm tọa độ điểm C đối xứng với M qua gốc O
- (4; 0)
- (4; -5)
- (0; 5)
- (-4; -5)
Câu 18: Phương trình tiếp tuyến d của đường tròn (C):(x + 2)2 + (y + 2)2 = 9 tại điểm M (2; 1) là:
- d: – y + 1 = 0
- d: 4x + 3y + 14 = 0
- d: 3x – 4y – 2 = 0
- d: 4x + 3y – 11 = 0
Câu 19: Phương trình tổng quát của đường thẳng d đi qua điểm M(2; 2) và có vectơ pháp tuyến = (1; 3) là:
- x + 3y – 6 = 0
- 3x + y – 8 = 0
- x + 3y – 8 = 0
- x + y – 3 = 0
Câu 20: Cho ba điểm A(1; 1), B(2; 4), C(4; 4). Tìm tọa độ điểm D sao cho ABCD là một hình bình hành.
- (4; 0)
- (4; -5)
- (1; 3)
- (-4; 5)
-----------Còn tiếp-----------
2. TRỌN BỘ ĐỀ THI TOÁN 10 CHÂN TRỜI SÁNG TẠO
Bộ đề Toán 10 Chân trời sáng tạo biên soạn đầy đủ gồm: đề thi + hướng dẫn chấm điểm, bảng năng lực và cấp độ tư duy, bảng đặc tả kĩ thuật
MA TRẬN KIỂM TRA TRẮC NGHIỆM KHÁCH QUAN
(30 câu – TN – 6 điểm, 5 câu – TL – 4 điểm)
TT | Nội dung kiến thức | Đơn vị kiến thức | Mức độ kiến thức, kĩ năng cần kiểm tra, đánh giá | Mức độ | |||
Nhận biết | Thông hiểu | Vận dụng | Vận dụng cao | ||||
1
|
Mệnh đề và tập hợp
| 1.1. Mệnh đề | Nhận biết: - Biết thế nào là một mệnh đề, mệnh đề phủ định, mệnh đề chứa biến. - Biết ý nghĩa kí hiệu phổ biến (") và kí hiệu tồn tại ($). - Biết được mệnh đề kéo theo, mệnh đề tương đương. Thông hiểu: - Lấy được ví dụ mệnh đề, phủ định một mệnh đề, xác định được tính đúng sai của các mệnh đề trong những trường hợp đơn giản. - Phân biệt được điều kiện cần và điều kiện đủ, giả thiết và kết luận. |
2 |
1 |
0 |
0 |
1.2. Tập hợp | Nhận biết: - Biết cho tập hợp bằng cách liệt kê các phần tử của tập hợp hoặc chỉ ra tính chất đặc trưng của các phần tử của tập hợp Thông hiểu: - Biểu diễn được các khoảng, đoạn trên trục số. - Lấy được ví dụ về tập hợp, tập hợp con, tập hợp bằng nhau. | 1 | 1 | 0 | 0 | ||
1.3. Các phép toán trên tập hợp | Nhận biết: - Hiểu được các kí hiệu ℕ*, ℕ, ℤ, ℚ, ℝ và mối quan hệ giữa các tập hợp đó. Thông hiểu: - Thực hiện được các phép toán giao của hai tập hợp, hợp của hai tập hợp, phần bù của một tập con. - Sử dụng đúng các kí hiệu Î, Ï, Ì, É, Æ, A\B, CEA. - Sử dụng đúng các kí hiệu (a; b); [a; b]; (a; b]; [a; b); (–¥; a); (–¥; a]; (a;+¥); [a; +¥); (– ¥; +¥). | 2 | 1 | 0 | 0 | ||
2
|
Bất phương trình và hệ bất phương trình bậc nhất hai ẩn
| 2.1 Bất phương trình bậc nhất hai ẩn | Nhận biết: Nhận biết được bất phương trình hai ẩn, nghiệm và tập hợp nghiệm của bất phương trình hai ẩn. Thông hiểu: Xác định được nghiệm, miền nghiệm của bất phương trình. | 2 | 1 | 0 | 0 |
2.2. Hệ bất phương trình bậc nhất hai ẩn | Nhận biết: Nhận biết được hệ bất phương trình hai ẩn, nghiệm và tập hợp nghiệm của hệ bất phương trình hai ẩn. Thông hiểu: Xác định được nghiệm, miền nghiệm của hệ bất phương trình hai ẩn. Vận dụng: Ý nghĩa của hệ bất phương trình hai ẩn thông qua các ví dụ thực tiễn. | 2 | 1 | 0 | 0 | ||
3
|
Hệ thức lượng trong tam giác
| 3.1 Giá trị lượng giác của một góc từ 00 đến 1800 | Nhận biết: - Nhận biết được giá trị lượng giác của một góc từ 0° đến 180°. - Tính được giá trị lượng giác của một góc từ 0° đến 180° bằng máy tính cầm tay. Thông hiểu: | 1 | 1 | 1 | 0 |
3.2 Định lí coossin và định lí sin | Nhận biết: Nhận biết và ghi nhớ định lí côsin và định lí sin, công thức tính diện tích tam giác. Thông hiểu: Giải thích được định lí côsin và định lí sin, công thức tính diện tích tam giác. | 2 | 1 | 0 | 0 | ||
3.3 Giải tam giác và ứng dụng thực tế | Nhận biết: Nhận biết và ghi nhớ cách giải tam giác. Thông hiểu: Mô tả và thực hiện được cách giải tam giác. Vận dụng: Vận dụng vào bài toán thực tiễn. | 2 | 2 | 0 | 0 | ||
4 |
Vectơ | 4.1 Khái niệm vectơ | Nhận biết : Nhận biết được các khái niệm của vectơ | 1 | 1 | 1 | 0 |
4.2 Tổng và hiệu của hai vectơ | Nhận biết: Nhận biết được những tính chất hình học của tổng và hiệu của hai vectơ. Thông hiểu: Mô tả và thực hiện được tổng và hiệu của hai vectơ. | 2 | 0 | 0 | 0 | ||
4.3. Tích của một số với một vectơ | Nhận biết: Nhận biết được tích của một số với một vectơ. Thông hiểu: Mô tả và thực hiện được tích của một số với một vectơ. | 2 | 2 | 0 | 0 | ||
4.4 Tích vô hướng của hai vectơ | Nhận biết: Nhận biết được những tính chất hình học của tổng và hiệu của hai vectơ. Thông hiểu: Mô tả và thực hiện được tổng và hiệu của hai vectơ. Vận dụng cao: Vận dụng được bài toán thực tiễn hoặc chứng minh đẳng thức liên quan. | 1 | 2 | 0 | 1 | ||
Tổng | 20 | 15 | 2 | 1 | |||
ĐỀ THI GIỮA HỌC KỲ 1
MÔN: TOÁN 10
I. TRẮC NGHIỆM (7 điểm)
Câu 1. Cho các câu sau đây:
a) Không được nói chuyện!
b) Ngày mai bạn đi học không?
c) Chủ tịch Hồ Chí Minh sinh năm 1890.
d) 22 chia 3 dư 1.
e) 2005 không là số nguyên tố.
Có bao nhiêu câu là mệnh đề ?
A. 1;
B. 2;
C. 3;
D. 4.
Câu 2. Cho hai mệnh đề P: “x là số chẵn” và Q: “x chia hết cho 2”.
Phát biểu mệnh đề P kéo theo Q.
A. Hoặc x là số chẵn hoặc x chia hết cho 2;
B. Nếu x là số chẵn thì x chia hết cho 2;
C. Nếu x chia hết cho 2 thì x là số chẵn;
D. x là số chẵn và x chia hết cho 2.
Câu 3. Cho tập hợp A là các nghiệm của phương trình x2 – 6x + 5 = 0.
Viết tập hợp trên dưới dạng liệt kê các phần tử.
A. A = {2 ; 3};
B. A = {1 ; 5};
C. A = {4 ; 6};
D. A = {2 ; 4}.
Câu 4. Cho tập hợp H = [1; 7] ∩ (– 3; 5). Đáp án nào sau đây là đúng.
A. H = [1; 7];
B. H = (– 3; 5);
C. H = [1; 5];
D. H = [1; 5).
Câu 5. Cho hai tập hợp A = (0; 3), B = (2; 4). Xác định A \ B.
A. A \ B = (0; 2];
B. A \ B = (0; 2);
C. A \ B = (0; 4);
D. A \ B = [3; 4).
Câu 6. Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
A. 2x – 4y + 7 ≥ 0;
B. 5x3 – 4y3 – 2 ≤ 0;
C. x3 – 2y < 0;
D. x2 + 3 > 0.
Câu 7. Cặp số (–1; 3) là một nghiệm của bất phương trình:
A. –3x + 2y – 4 > 0;
B. x + 3y < 0;
C. 3x – y > 0;
D. 2x – y + 4 > 0.
Câu 8. Trong các hệ bất phương trình sau, đâu không là hệ bất phương trình bậc nhất hai ẩn:
A. ![]() ;
;
B.  ;
;
C. 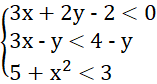 ;
;
D. ![]()
Câu 9. Trong các đẳng thức sau đây, đẳng thức nào đúng?
A. sin60° = ![]() ;
;
B. cos60° = ![]() ;
;
C. tan60° = 1;
D. cot60° = −1.
Câu 10. Cho α là góc nhọn. Khẳng định nào sau đây là đúng?
A. sin α < 0;
B. cos α < 0;
C. tan α < 0;
D. cot α > 0.
Câu 11. Chọn đáp án sai: Một tam giác giải được nếu biết:
A. Độ dài 3 cạnh;
B. Độ dài 2 cạnh và 1 góc bất kỳ;
C. Số đo 3 góc;
D. Độ dài 1 cạnh và 2 góc bất kỳ.
Câu 12. Cho hình vuông ABCD tâm O. Giá của vectơ AO là:
A. Đường thẳng AC;
B. Đường thẳng BC;
C. Đường thẳng AB;
D. Đường thẳng DO.
-----------Còn tiếp-----------

Đủ kho tài liệu môn học
=> Tài liệu sẽ được gửi ngay và luôn
Cách tải:
- Bước 1: Chuyển phí vào STK: 1214136868686 - cty Fidutech - MB
- Bước 2: Nhắn tin tới Zalo Fidutech - nhấn vào đây để thông báo và nhận tài liệu
=> Giáo án toán 10 chân trời sáng tạo (bản word)
Từ khóa: Giáo án và PPT đồng bộ Toán 10 chân trời sáng tạo, soạn giáo án word và powerpoint Toán 10 chân trời sáng tạo, soạn Toán 10 chân trời sáng tạoTài liệu giảng dạy môn Toán THPT
