Giáo án ppt kì 2 Toán 9 cánh diều
Đầy đủ giáo án PPT, điện tử, bài giảng kì 2, giáo án cả năm Toán 9 cánh diều. Bộ giáo án hoàn thiện, sinh động, hấp dẫn, được hỗ trợ tốt nhất hiện nay. Khi mua giáo án được tặng thêm: bộ phiếu trắc nghiệm, tự luận, bộ đề kiểm tra theo cấu trúc mới. Bài giảng được gửi ngay và luôn. Có thể xem tham khảo bất kì bài nào phía dưới trước khi mua.
Một số tài liệu quan tâm khác
Phần trình bày nội dung giáo án
I. SLIDE ĐIỆN TỬ KÌ 2 TOÁN 9 CÁNH DIỀU
- Giáo án điện tử Toán 9 cánh diều Bài 1: Mô tả và biểu diễn dữ liệu trên các bảng, biểu đồ
- Giáo án điện tử Toán 9 cánh diều Bài 2: Tần số. Tần số tương đối
- Giáo án điện tử Toán 9 cánh diều Bài 3: Tần số ghép nhóm. Tần số tương đối ghép nhóm
- Giáo án điện tử Toán 9 cánh diều Bài 4: Phép thử ngẫu nhiên và không gian mẫu. Xác suất của biến cố
- Giáo án điện tử Toán 9 cánh diều Bài tập cuối chương VI
- Giáo án điện tử Toán 9 cánh diều Hoạt động thực hành và trải nghiệm Chủ đề 2: Mật độ dân số
- Giáo án điện tử Toán 9 cánh diều Bài 1: Hàm số y = ax^2 (a ≠ 0)
- Giáo án điện tử Toán 9 cánh diều Bài 2: Phương trình bậc hai một ẩn
- Giáo án điện tử Toán 9 cánh diều Bài 3: Định lí Viète
- Giáo án điện tử Toán 9 cánh diều Bài tập cuối chương VII
- Giáo án điện tử Toán 9 cánh diều Bài 1: Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác
- Giáo án điện tử Toán 9 cánh diều Bài 2: Tứ giác nội tiếp đường tròn
- Giáo án điện tử Toán 9 cánh diều Bài tập cuối chương VIII
- Giáo án điện tử Toán 9 cánh diều Bài 1: Đa giác đều. Hình đa giác đều trong thực tiễn
- Giáo án điện tử Toán 9 cánh diều Bài 2: Phép quay
- Giáo án điện tử Toán 9 cánh diều Bài tập cuối chương IX
- Giáo án điện tử Toán 9 cánh diều Bài 1: Hình trụ
- Giáo án điện tử Toán 9 cánh diều Bài 2: Hình nón
- Giáo án điện tử Toán 9 cánh diều Bài 3: Hình cầu
- Giáo án điện tử Toán 9 cánh diều Bài tập cuối chương X
- Giáo án điện tử Toán 9 cánh diều Hoạt động thực hành và trải nghiệm Chủ đề 3: Tạo đồ dùng dạng hình nón, hình trụ
- Giáo án điện tử Toán 9 cánh diều Bài Thực hành phần mềm GeoGebra
CHÀO MỪNG CẢ LỚP ĐẾN VỚI BUỔI HỌC HÔM NAY!
KHỞI ĐỘNG

Đội văn nghệ của lớp 9A có 3 bạn nam và 3 bạn nữ. Cô giáo phụ trách đội chọn ngẫu nhiên hai bạn từ 6 bạn đó để hát song ca. Xét biến cố sau: “Trong 2 bạn được chọn ra, có 1 bạn nam và 1 bạn nữ”.
- Làm thế nào để tính được xác suất của biến cố ngẫu nhiên nói trên?
BÀI 4. PHÉP THỬ NGẪU NHIÊN VÀ KHÔNG GIAN MẪU XÁC SUẤT CỦA BIẾN CỐ
NỘI DUNG BÀI HỌC
Phép thử ngẫu nhiên và không gian mẫu
Xác suất của biến cố
I. PHÉP THỬ NGẪU NHIÊN VÀ KHÔNG GIAN MẪU
HĐ1
a) Hãy thực hiện hành động: Tung một đồng xu một lần.
b) Xét phép thử “Tung một đồng xu một lần”.
Viết tập hợp Ω (đọc là: ô-mê-ga) gồm các kết quả có thể xảy ra đối với mặt xuất hiện của đồng xu. Tập hợp Ω có bao nhiêu phần tử?
Giải
a) HS thực hiện hành động tung một đồng xu.
b) Ta có Ω = {Sấp; Ngửa}.
Tập hợp Ω có 2 phần tử.
Ghi nhớ
Có những phép thử mà tập hợp gồm các kết quả có thể xảy ra của phép thử đó hoàn toàn xác định. Tuy nhiên, các kết quả xảy ra có tính ngẫu nhiên, ta không thể đoán trước được. Những phép thử như thế gọi là phép thử ngẫu nhiên (gọi tắt là phép thử) và tập hợp gọi là không gian mẫu của phép thử.
CHÚ Ý
- Các kết quả có thể xảy ra của một phép thử có khả năng xuất hiện như nhau được gọi là đồng khả năng.
- Kết quả thuận lợi cho biến cố A là một kết quả có thể của phép thử làm cho biến cố A xảy ra.
Ví dụ 1: Xét phép thử “Gieo một xúc xắc một lần”.
a) Nêu những kết quả có thể xảy ra đối với mặt xuất hiện của xúc xắc.
b) Viết không gian mẫu của phép thử đó.
Giải
a) Các kết quả có thể xảy ra đối với mặt xuất hiện của xúc xắc là: mặt 1 chấm; mặt 2 chấm; mặt 3 chấm; mặt 4 chấm; mặt 5 chấm; mặt 6 chấm.
b) Không gian mẫu của phép thử đó là:
mặt 1 chấm; mặt 2 chấm; mặt 3 chấm; mặt 4 chấm; mặt 5 chấm; mặt 6 chấm
Luyện tập 1
Một hộp có 12 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, ..., 12; hai thẻ khác nhau thì ghi hai số khác nhau. Xét phép thử “Rút ngẫu nhiên một thẻ trong hộp”.
a) Nêu những kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra.
b) Viết không gian mẫu của phép thử đó.
Giải
a) Những kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra là: số 1; số 2; số 3; số 4; số 5; số 6; số 7; số 8; số 9; số 10; số 11; số 12.
b) Không gian mẫu của phép thử là:
Ω = {Số 1; số 2; số 3; số 4; số 5; số 6; số 7; số 8; số 9; số 10;
số 11; số 12}.
II. XÁC SUẤT CỦA BIẾN CỐ
HĐ2
Hình 27 mô tả một đĩa tròn bằng bìa cứng được chia làm 12 phần bằng nhau và ghi các số 1, 2, 3, ..., 12; chiếc kim được gắn cố định vào trục quay ở tâm của đĩa. Xét phép thử “Quay đĩa tròn một lần”.
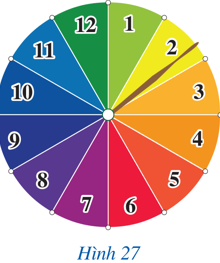
a) Viết tập hợp gồm các kết quả có thể xảy ra đối với số ghi ở hình quạt mà chiếc kim chỉ vào khi đĩa dừng lại.
b) Liệt kê các kết quả thuận lợi cho biến cô : “Chiếc kim chỉ vào hình quạt ghi số chia hết cho 3”.
c) Tìm tỉ số giữa số các kết quả thuận lợi cho biến cố và số phần tử của tập hợp .
Giải
a) Tập hợp gồm các kết quả có thể xảy ra đối với số ghi ở hình quạt mà chiếc kim chỉ vào khi đĩa dừng lại là:
Ω = {1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12}.
b) Trong các số 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12, có 3 số chia hết cho 3 là: 3; 6; 9; 12.
Do đó các kết quả thuận lợi cho biến cố A là 3; 6; 9; 12.
c) Tỉ số giữa số các kết quả thuận lợi cho biến cố A và số phần tử của tập hợp Ω là 4/12=1/3
KẾT LUẬN
Giả thiết rằng các kết quả có thể xảy ra của một phép thử là đồng khả năng.
Khi đó, xác suất của biến cố , kí hiệu là , bằng tỉ số giữa số kết quả thuận lợi cho biến cố và tổng số kết quả có thể xảy ra:

Nhận xét: Để tính xác suất của biến cố , ta có thể thực hiện các bước sau:
Bước 1. Kiểm tra tính đồng khả năng đối với các kết quả có thể xảy ra của phép thử
Bước 2. Đếm số kết quả có thể xảy ra, tức là đếm số phần tử của không gian mẫu
Bước 3. Đếm số kết quả thuận lợi cho biến cố
Bước 4. Lập tỉ số giữa số kết quả thuận lợi cho biến cố và tổng số kết quả có thể xảy ra.
----------------------------------
----------------------- Còn tiếp -------------------------
CHÀO MỪNG CÁC EM
ĐÃ ĐẾN VỚI BUỔI HỌC!
KHỞI ĐỘNG
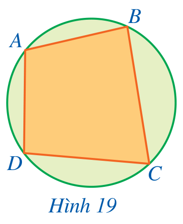
Hình 19 minh họa một đường tròn và tứ giác có bốn đỉnh thuộc đường tròn.
Tứ giác ABCD được gọi là gì?
BÀI 2. TỨ GIÁC NỘI TIẾP ĐƯỜNG TRÒN
NỘI DUNG BÀI HỌC
Định nghĩa
Tính chất
Hình chữ nhật, hình vuông nội tiếp đường tròn
I. ĐỊNH NGHĨA
HĐ 1
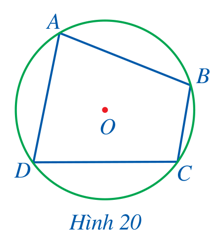
Quan sát Hình 20 và cho biết các đỉnh của tứ giác có thuộc đường tròn hay không.
Giải
Ở hình 20, các đỉnh A, B, C,D của tứ giác ABCD đều thuộc đường tròn (O).
Ghi nhớ
Tứ giác có bốn đỉnh thuộc một đường tròn được gọi là tứ giác nội tiếp đường tròn (hay còn gọi là tứ giác nội tiếp).
Chú ý: Trong hình 20, tứ giác ABCD là tứ giác nội tiếp và đường tròn (O) được gọi là đường tròn ngoại tiếp tứ giác ABCD.
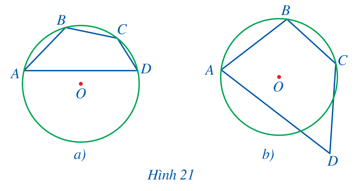
Ví dụ 1: Trong các hình 21a, 21b, ở hình nào ta có tứ giác nội tiếp đường tròn ? Vì sao?
Giải
- Ở Hình 21a, đường tròn (O) là đường tròn ngoại tiếp tứ giác ABCD vì nó đi qua cả bốn đỉnh A, B, C, D của tứ giác đó.
- Ở Hình 21b, đường tròn (O) không là đường tròn ngoại tiếp tứ giác ABCD vì nó không đi qua cả đỉnh D của tứ giác đó.
Luyện tập 1
Dùng thước thẳng và compa vẽ một tứ giác nội tiếp đường tròn theo các bước sau:
- Vẽ một đường tròn.
- Vẽ tứ giác có bốn đỉnh thuộc đường tròn.
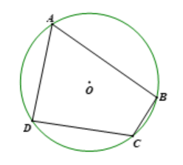
Giải
Vẽ đường tròn (O), lấy 4 điểm A, B, C, D (theo thứ tự cùng chiều kim đồng hồ) thuộc đường tròn (O) và nối các đoạn thẳng AB, BC, CD, DA thì ta được tứ giác ABCD có bốn đỉnh thuộc đường tròn (O).
II. TÍNH CHẤT
HĐ 2
Trong Hình 22, cho biết (AOC) ̂=α.
Tính số đo của các cung và góc sau theo α:
a) (ADC) ̂, (ABC) ̂; b) (ABC) ̂, (ADC) ̂; c) (ADC) ̂+(ABC) ̂
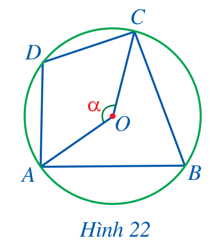
Giải
a) Xét đường tròn (O) có:
(AOC) ̂ là góc ở tâm chắn cung ADC nên sđ⏜ADC=(AOC) ̂=α.
(ABC) ̂ là góc nội tiếp chắn cung ADC nên (ABC) ̂=1/2 sđ⏜ADC=1/2 α.
b) Xét đường tròn (O) có:
sđ⏜ABC=360°-sđ⏜ADC=360°-α.
(ADC) ̂ là góc nội tiếp chắn cung ABC nên (ADC) ̂=1/2 sđ⏜ABC=1/2(360°-α).
c) Ta có: (ADC) ̂+(ABC) ̂=1/2 (360°-α)+1/2 α
=1/2 (360°-α+α)=1/2.360°=180°
Vậy (ADC) ̂+(ABC) ̂=180°.
KẾT LUẬN
Trong một tứ giác nội tiếp đường tròn, tổng số đo hai góc đối bằng 180^O
Ví dụ 2: Tìm α trong Hình 23.
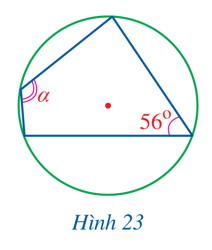
Giải
Từ Hình 23, ta có α+56^o=180^o (tổng hai góc đối của tứ giác nội tiếp).
Suy ra α=180^o-56^o
α=124^o .
----------------------------------
----------------------- Còn tiếp -------------------------
II. BÀI TẬP TỰ LUẬN KÌ 2 TOÁN 9 CÁNH DIỀU
- Bài tập file word Toán 9 cánh diều Bài 1: Mô tả và biểu diễn dữ liệu trên các bảng, biểu đồ
- Bài tập file word Toán 9 cánh diều Bài 2: Tần số. Tần số tương đối
- Bài tập file word Toán 9 cánh diều Bài 3: Tần số ghép nhóm. Tần số tương đối ghép nhóm
- Bài tập file word Toán 9 cánh diều Bài 4: Phép thử ngẫu nhiên và không gian mẫu. Xác suất của biến cố
- Bài tập file word Toán 9 cánh diều Thực hành trải nghiệm Chủ đề 2: Mật độ dân số
- Bài tập file word Toán 9 cánh diều Bài 1: Hàm số y = ax^2 (a ≠ 0)
- Bài tập file word Toán 9 cánh diều Bài 2: Phương trình bậc hai một ẩn
- Bài tập file word Toán 9 cánh diều Bài 3: Định lí Viète
- Bài tập file word Toán 9 cánh diều Bài 1: Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác
- Bài tập file word Toán 9 cánh diều Bài 2: Từ giác nội tiếp đường tròn
- Bài tập file word Toán 9 cánh diều Bài 1: Đa giác đều. Hình đa giác đều trong thực tiễn
- Bài tập file word Toán 9 cánh diều Bài 2: Phép quay
- Bài tập file word Toán 9 cánh diều Bài 1: Hình trụ
- Bài tập file word Toán 9 cánh diều Bài 2: Hình nón
- Bài tập file word Toán 9 cánh diều Bài 3: Hình cầu
- Bài tập file word Toán 9 cánh diều Thực hành trải nghiệm Chủ đề 3: Tạo đồ dùng dạng hình nón, hình trụ
CHƯƠNG 7: HÀM SỐ 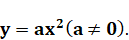 PHƯƠNG TRÌNH BẬC HAI MỘT ẨN
PHƯƠNG TRÌNH BẬC HAI MỘT ẨN
BÀI 1: HÀM SỐ 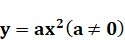
(17 câu)
1. NHẬN BIẾT (4 câu)
Câu 1: Trình bày các bước để vẽ đồ thị hàm số ![]()
Trả lời:
Để vẽ đồ thị của hàm số ![]() , ta thực hiện các bước sau:
, ta thực hiện các bước sau:
Bước 1. Lập bảng giá trị để tìm giá trị của ![]() tương ứng với một số giá trị cụ thể của
tương ứng với một số giá trị cụ thể của ![]()
Bước 2. Căn cứ vào bảng giá trị, vẽ một số điểm thuộc đồ thị của hàm số đó
Bước 3. Vẽ parabol đi qua gốc tọa độ và các điểm đã xác định ở bước 2, ta nhận được đồ thì của hàm số ![]()
Câu 2: Cho hàm số ![]() .Tìm giá trị của
.Tìm giá trị của ![]() tương ứng với giá trị của
tương ứng với giá trị của ![]() trong bảng như sau:
trong bảng như sau:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Trả lời:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Câu 3: Cho hàm số ![]()
a) Tìm giá trị của hàm số khi ![]() nhận các giá trị lần lượt là
nhận các giá trị lần lượt là ![]()
b) Tìm các giá trị của ![]() , biết rằng
, biết rằng ![]()
Trả lời:
a) Ta có: ![]()
b) Ta có: ![]()
Câu 4: Cho hàm số ![]() . Tìm những điểm thuộc đồ thị của hàm số có tung độ là
. Tìm những điểm thuộc đồ thị của hàm số có tung độ là ![]() .
.
Trả lời:
Thay ![]() vào đồ thị của hàm số
vào đồ thị của hàm số ![]() ta được:
ta được:
![]()
![]()
![]() và
và ![]()
Vậy có hai điểm ![]() thuộc đồ thị hàm số có tung độ bằng
thuộc đồ thị hàm số có tung độ bằng ![]()
2. THÔNG HIỂU (4 câu)
Câu 1: Cho hàm số ![]() . Tìm điều kiện của
. Tìm điều kiện của ![]() biết rằng
biết rằng ![]() .
.
Trả lời:
Ta có: ![]()
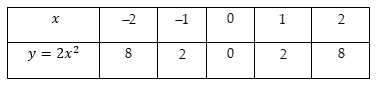
Câu 2: Vẽ đồ thị của hàm số ![]() .
.
Trả lời:
- Bảng giá trị của ![]() tương ứng với giá trị của
tương ứng với giá trị của ![]() như sau:
như sau:
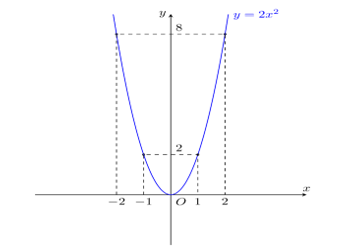
- Vẽ các điểm ![]() thuộc đồ thị hàm số
thuộc đồ thị hàm số ![]() trong mặt phẳng
trong mặt phẳng ![]() .
.
- Vẽ đường parabol đi qua các điểm trên, ta nhận được đồ thị của hàm số ![]()
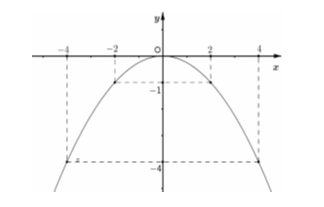
Câu 3: Cho hàm số: ![]() có đồ thị
có đồ thị ![]() . Vẽ đồ thị
. Vẽ đồ thị ![]() .
.
Trả lời:
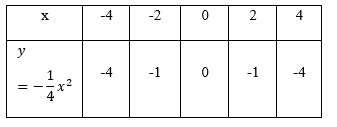
- Bảng giá trị của ![]() tương ứng với giá trị của
tương ứng với giá trị của ![]() như sau:
như sau:
- Vẽ các điểm ![]() thuộc đồ thị hàm số
thuộc đồ thị hàm số ![]() trong mặt phẳng
trong mặt phẳng ![]() .
.
- Vẽ đường parabol đi qua các điểm trên, ta nhận được đồ thị của hàm số ![]()
----------------------------------
----------------------- Còn tiếp -------------------------
CHƯƠNG 8: ĐƯỜNG TRÒN NGOẠI TIẾP VÀ ĐƯỜNG TRÒN NỘI TIẾP BÀI 1: ĐƯỜNG TRÒN NGOẠI TIẾP TAM GIÁC. ĐƯỜNG TRÒN NỘI TIẾP TAM GIÁC
(13 câu)
1. NHẬN BIẾT (4 câu)
Câu 1: Cho hình vẽ sau :
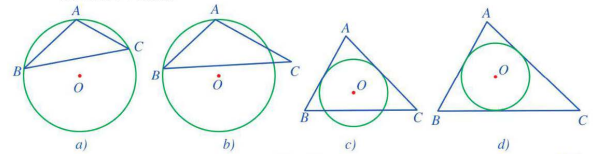
a) Hình nào có đường tròn ![]() ngoại tiếp tam giác
ngoại tiếp tam giác ![]() ?
?
b) Hình nào có đường tròn ![]() nội tiếp tam giác
nội tiếp tam giác![]() ?
?
Trả lời:
a) Hình ![]()
b) Hình ![]()
Câu 2: Nêu công thức tính bán kính đường tròn ngoại tiếp của tam giác đều cạnh là a ?
Trả lời:
Tam giác đều cạnh ![]() có bán kính đường tròn ngoại tiếp là
có bán kính đường tròn ngoại tiếp là ![]()
Câu 3: Nêu công thức tính bán kính đường tròn nội tiếp của tam giác đều cạnh là a ?
Trả lời:
Tam giác đều cạnh ![]() có bán kính đường tròn nội tiếp là
có bán kính đường tròn nội tiếp là ![]()
Câu 4: Cho tam giác ![]() vuông tại
vuông tại ![]() , có
, có ![]() và
và ![]() . Tính bán kính đường tròn ngoại tiếp tam giác
. Tính bán kính đường tròn ngoại tiếp tam giác ![]() .
.
Trả lời:
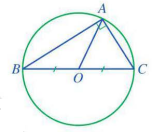
Xét ![]() vuông tại
vuông tại ![]() , theo pythagore ta có:
, theo pythagore ta có:
![]()
![]()
![]()
![]()
Tam giác ![]() vuông tại
vuông tại ![]() nên bán kính
nên bán kính ![]() đường tròn ngoại tiếp tam giác
đường tròn ngoại tiếp tam giác ![]() bằng nữa cạnh huyền
bằng nữa cạnh huyền ![]() hay
hay ![]()
2. THÔNG HIỂU (3 câu)
Câu 1: Cho ![]() vuông tại
vuông tại ![]() , có
, có ![]() và
và ![]() ngoại tiếp đường tròn
ngoại tiếp đường tròn ![]() . Tính
. Tính ![]()
Trả lời:
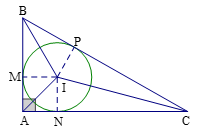
Đường tròn ![]() tiếp xúc với các cạnh
tiếp xúc với các cạnh ![]() theo thứ tự
theo thứ tự ![]()
Ta có: ![]()
Cộng ![]() vế theo vế, ta được:
vế theo vế, ta được: ![]()
Mà ![]() ,
, ![]()
Nên ta có: ![]() .
.
Câu 2: Ba đường tròn tiếp xúc với nhau từng đôi một và tiếp xúc với các cạnh của tam giác như hình bên. Nếu mỗi đường tròn có bán kính là 3, thì chu vi của tam giác sẽ bằng bao nhiêu?
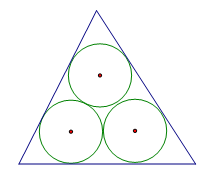
Trả lời:
Từ tâm ![]() và
và ![]() vẽ
vẽ ![]() và
và ![]() vuông góc với cạnh
vuông góc với cạnh ![]() của tam giác
của tam giác
Các tam giác ![]() và
và ![]() là nửa tam giác đều với
là nửa tam giác đều với ![]()
![]()
Vậy chu vi tam giác là: ![]()
----------------------------------
----------------------- Còn tiếp -------------------------

Đủ kho tài liệu môn học
=> Tài liệu sẽ được gửi ngay và luôn
Cách tải:
- Bước 1: Chuyển phí vào STK: 1214136868686 - cty Fidutech - MB
- Bước 2: Nhắn tin tới Zalo Fidutech - nhấn vào đây để thông báo và nhận tài liệu
