Giáo án ppt kì 2 Toán 9 kết nối tri thức
Đầy đủ giáo án PPT, điện tử, bài giảng kì 2, giáo án cả năm Toán 9 kết nối tri thức. Bộ giáo án hoàn thiện, sinh động, hấp dẫn, được hỗ trợ tốt nhất hiện nay. Khi mua giáo án được tặng thêm: bộ phiếu trắc nghiệm, tự luận, bộ đề kiểm tra theo cấu trúc mới. Bài giảng được gửi ngay và luôn. Có thể xem tham khảo bất kì bài nào phía dưới trước khi mua.
Một số tài liệu quan tâm khác
Phần trình bày nội dung giáo án
I. SLIDE ĐIỆN TỬ KÌ 2 TOÁN 9 KẾT NỐI TRI THỨC
- Giáo án điện tử Toán 9 kết nối Bài 18: Hàm số y = ax^2 (a ≠ 0)
- Giáo án điện tử Toán 9 kết nối Bài 19: Phương trình bậc hai một ẩn
- Giáo án điện tử Toán 9 kết nối Chương 6 Luyện tập chung (1)
- Giáo án điện tử Toán 9 kết nối Bài 20: Định lí Viète và ứng dụng
- Giáo án điện tử Toán 9 kết nối Bài 21: Giải bài toán bằng cách lập phương trình
- Giáo án điện tử Toán 9 kết nối Chương 6 Luyện tập chung (2)
- Giáo án điện tử Toán 9 kết nối Bài tập cuối chương VI
- Giáo án điện tử Toán 9 kết nối Bài 22: Bảng tần số và biểu đồ tần số
- Giáo án điện tử Toán 9 kết nối Bài 23: Bảng tần số tương đối và biểu đồ tần số tương đối
- ………………
- Giáo án điện tử Toán 9 kết nối Bài 31: Hình trụ và hình nón
- Giáo án điện tử Toán 9 kết nối Bài 32: Hình cầu
- Giáo án điện tử Toán 9 kết nối Chương 10 Luyện tập chung
- Giáo án điện tử Toán 9 kết nối Bài tập cuối chương X
- Giáo án điện tử Toán 9 kết nối Hoạt động thực hành trải nghiệm: Giải phương trình, hệ phương trình và vẽ đồ thị hàm số với phần mềm GeoGebra
- Giáo án điện tử Toán 9 kết nối Hoạt động thực hành trải nghiệm: Vẽ hình đơn giản với phần mềm GeoGebra
- Giáo án điện tử Toán 9 kết nối Hoạt động thực hành trải nghiệm: Xác định tần số, tần số tương đối, vẽ các biểu đồ biểu diễn bảng tần số, tần số tương đối bằng Excel
- Giáo án điện tử Toán 9 kết nối Hoạt động thực hành trải nghiệm: Gene trội trong các thế hệ lai
- Giáo án điện tử Toán 9 kết nối Bài tập ôn tập cuối năm
CHÀO MỪNG CÁC EM ĐẾN VỚI TIẾT HỌC MÔN TOÁN!
KHỞI ĐỘNG
Với dãy dữ liệu ![]() có nhiều giá trị giống nhau thì có cách nào biểu diễn dãy dữ liệu này thuận tiện hơn không? Chúng ta sẽ tìm hiểu vấn đề này trong bài học
có nhiều giá trị giống nhau thì có cách nào biểu diễn dãy dữ liệu này thuận tiện hơn không? Chúng ta sẽ tìm hiểu vấn đề này trong bài học
CHƯƠNG VII.
TẦN SỐ VÀ TẦN SỐ TƯƠNG ĐỐI
BÀI 22. BẢNG TẦN SỐ VÀ BIỂU ĐỒ TẦN SỐ
NỘI DUNG BÀI HỌC
01 BẢNG TẦN SỐ
HĐ1
Bạn Minh muốn tìm hiểu về dự định của các bạn học sinh khối lớp 9 trong trường sau khi tốt nghiệp Trung học cơ sở. Em hãy giúp bạn Minh thực hiện khảo sát ý kiến của các bạn trong lớp mình theo mẫu phiếu bên.
a) Bạn Minh muốn khảo sát ý kiến của những ai? Em đã giúp bạn Minh khảo sát ý kiến của tất cả những người đó?
b) Liệt kê dãy dữ liệu thu được và đếm số học sinh theo mỗi lựa chọn.

Giải
a) Bạn Minh muốn khảo sát ý kiến của tất cả các bạn học sinh khối 9 trong trường.
b) Ví dụ
A. Học trung học phổ thông trong nước: 35 bạn
B. Đi du học: 0 bạn
C. Đi học nghề: 10 bạn
D. Lựa chọn khác: 0 bạn
NHẬN XÉT
Dữ liệu mà bạn Minh muốn có là dữ liệu về ý kiến của tất cả học sinh khối lớp 9 trong trường. Dãy dữ liệu mà em thu được trong khảo sát trên là một phần của dữ liệu bạn Minh muốn có và được gọi là mẫu dữ liệu. Số giá trị của mẫu dữ liệu được gọi là cỡ mẫu.
GHI NHỚ
+ Tần số của một giá trị là số lần xuất hiện giá trị đó trong mẫu dữ liệu.
+ Bảng tần số là bảng thống kê cho biết tần số của các giá trị trong mẫu dữ liệu. Bảng tần số có dạng sau:
| Giá trị | …. | |||
| Tần số | …. |
Trong đó ![]() là tần số của
là tần số của ![]() là tần số của
là tần số của ![]() ….,
…., ![]() là tần số của
là tần số của ![]() .
.
Lập bảng tần số cho mẫu dữ liệu thu được trong HĐ1.
Giải
| Dự định | Học THPT trong nước | Đi du học | Đi học nghề | Lựa chọn khác |
| Tần số | 35 | 0 | 10 | 0 |
Ví dụ 1
Để mua giày thể thao cho các bạn nam trong lớp luyện tập chuẩn bị cho giải bóng đá của trường, Huy đã thu thập cỡ giày của các bạn nam trong lớp và thu được kết quả như sau:
40, 36, 37, 36, 40, 38, 39, 38, 37, 36, 40, 39, 36, 38, 37, 38, 38, 37, 38, 38, 38, 36.
a) Bạn Huy cần mua giày các cỡ nào? Mỗi loại bao nhiêu đôi?
b) Lập bảng tần số cho dãy dữ liệu trên. Từ bảng tần số, cho biết cỡ giày nào phù hợp với nhiều bạn nam trong lớp nhất.
Giải
a) Bạn Huy cần mua giày với các cỡ 36, 37, 38, 39, 40. Giày cỡ 36 cần 5 đôi; cỡ 37 cần 4 đôi; cỡ 38 cần 8 đôi; cỡ 39 cần 2 đôi; cỡ 40 cần 3 đôi.
b) Bảng tần số:
| Cỡ giày | 36 | 37 | 38 | 39 | 40 |
| Tần số | 5 | 4 | 8 | 2 | 3 |
> Giày cỡ 38 phù hợp với nhiều bạn nam trong lớp nhất.
Luyện tập 1
Bảng sau đây ghi lại tên các bạn đạt điểm tốt vào các ngày trong tuần của lớp 9E, mỗi điểm tốt ghi tên một lần.
| Ngày | Thứ Hai | Thứ Ba | Thứ Tư | Thứ Năm | Thứ Sáu |
| Tên bạn đạt điểm tốt | Bình Nam | Tuấn Thảo | Bình | Yến Nam | Nam Thảo |
a) Trong tuần những bạn nào đạt điểm tốt? Mỗi bạn đạt được mấy điểm tốt?
b) Lập bảng tần số cho dãy dữ liệu này. Bạn nào có số lần đạt điểm tốt nhiều nhất?
Giải
a) Các bạn đạt điểm tốt trong tuần là: Bình, Tuấn, Nam, Yến, Thảo.
Bình được 2 điểm tốt, Tuấn được 1 điểm tốt, Nam được 3 điểm tốt, Yến được 1 điểm tốt, Thảo được 2 điểm tốt.
b) Bảng tần số
| Tên học sinh | Bình | Nam | Tuấn | Thảo | Yến |
| Tần số | 2 | 3 | 1 | 2 | 1 |
> Nam đạt được điểm tốt nhiều lần nhất, với 3 lần.
NHẬN XÉT
Trong bảng tần số, ta chỉ liệt kê các giá trị ![]() khác nhau. Các giá trị
khác nhau. Các giá trị ![]() này có thể không là số.
này có thể không là số.
Tần số của một giá trị cho biết giá trị đó xuất hiện trong mẫu dữ liệu nhiều hay ít, từ đó ta dễ dàng xác định được giá trị xuất hiện nhiều nhất, ít nhất.
02 BIỂU ĐỒ TẦN SỐ
------------------------- Còn tiếp -------------------------
CHÀO MỪNG TẤT CẢ CÁC EM ĐẾN VỚI BÀI HỌC HÔM NAY!
KHỞI ĐỘNG
Cho trước một tam giác ABC. Bằng thước kẻ và compa, em có thể vẽ được một đường tròn đi qua ba đỉnh của tam giác và đường tròn tiếp xúc với ba cạnh của tam giác hay không?
BÀI 28. ĐƯỜNG TRÒN NGOẠI TIẾP VÀ ĐƯỜNG TRÒN NỘI TIẾP CỦA MỘT TAM GIÁC
NỘI DUNG BÀI HỌC

1 ĐƯỜNG TRÒN NGOẠI TIẾP MỘT TAM GIÁC
Khái niệm đường tròn ngoại tiếp tam giác
HĐ 1
Cho d là đường trung trực của đoạn thẳng AB và O là một điểm trên d (H.9.12). Hỏi đường tròn tâm O đi qua A thì có đi qua B không?
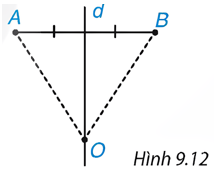
Giải
Vì ![]() nằm trên đường trung trực
nằm trên đường trung trực ![]() của đoạn thẳng
của đoạn thẳng ![]() nên
nên ![]() .
.
Do đó đường tròn tâm ![]() đi qua
đi qua ![]() cũng đi qua
cũng đi qua ![]() .
.
HĐ 2
Cho tam giác ABC có ba đường trung trực đồng quy tại O (H.9.13). Hãy giải thích tại sao đường tròn (O; OA) đi qua ba đỉnh của tam giác ABC.
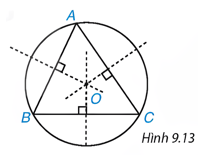
Giải:
Vì ![]() là giao điểm 3 đường trung trực nên
là giao điểm 3 đường trung trực nên ![]() , nên đường tròn
, nên đường tròn ![]() đi qua ba đỉnh của tam giác
đi qua ba đỉnh của tam giác ![]() .
.
ĐỊNH NGHĨA
Đường tròn ngoại tiếp một tam giác là đường tròn đi qua ba đỉnh của tam giác đó.
Hãy kể tên bốn tam giác nội tiếp đường tròn (O) trong Hình 9.14.
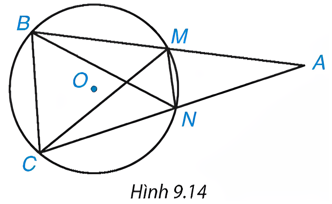
Giải
+ Các tam giác: ![]() .
.
+ Tam giác ![]() không nội tiếp đường tròn
không nội tiếp đường tròn ![]() .
.
Đường tròn ngoại tiếp tam giác vuông
HĐ 3
Cho tam giác ABC vuông tại đỉnh A. Gọi N, P lần lượt là trung điểm của các cạnh AB và AC (H.9.15).
a) Vẽ hai đường trung trực a, b của các cạnh AB, AC, cắt nhau tại M.
b) Hãy giải thích vì sao MN, MP là các đường trung bình của tam giác ABC.
c) Hãy giải thích vì sao M là trung điểm của BC, từ đó suy ra đường tròn ngoại tiếp của tam giác ABC có tâm M và bánh kính ![]() .
.
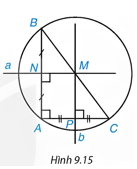
Giải:
b) Ta có ![]() (do cùng vuông góc với
(do cùng vuông góc với ![]() ) và
) và ![]() là trung điểm
là trung điểm ![]() nên
nên ![]() là đường trung bình của tam giác
là đường trung bình của tam giác ![]()
Tương tự ta cũng có ![]() là đường trung bình của tam giác
là đường trung bình của tam giác ![]() .
.
c) Do ![]() là đường trung bình của tam giác
là đường trung bình của tam giác ![]() nên
nên ![]() là trung điểm
là trung điểm ![]() . Từ đó, do
. Từ đó, do ![]() là trung trực của đoạn
là trung trực của đoạn ![]() nên
nên ![]() .
.
Vậy ![]() là tâm đường tròn ngoại tiếp tam giác
là tâm đường tròn ngoại tiếp tam giác ![]() và
và ![]() .
.
ĐỊNH NGHĨA
Đường tròn ngoại tiếp tam giác vuông có tâm là trung điểm của cạnh huyển và bán kính bằng một nửa cạnh huyền.
Ví dụ 1: Cho tam giác ABC vuông tại A có ![]() ,
, ![]() . Vẽ đường tròn
. Vẽ đường tròn ![]() ngoại tiếp tam giác ABC và tính bán kính R.
ngoại tiếp tam giác ABC và tính bán kính R.
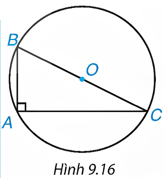
Lấy O là trung điểm của BC và vẽ đường tròn (O) đi qua A.
Khi đó, (O) là đường tròn ngoại tiếp tam giác ABC.
Theo định lí Pythagore, ta có:
![]() nên
nên ![]() (cm)
(cm)
Vậy đường tròn (O) có bán kính ![]() cm
cm
Luyện tập 1
Cho tam giác ABC có ![]() ,
, ![]() và
và ![]() . Tính bán kính của đường tròn ngoại tiếp tam giác ABC.
. Tính bán kính của đường tròn ngoại tiếp tam giác ABC.
Giải
Tam giác ![]() có
có
![]()
nên ![]() là tam giác vuông.
là tam giác vuông.
Suy ra bán kính đường tròn ngoại tiếp tam giác ![]() là 2,5 cm.
là 2,5 cm.
Đường tròn ngoại tiếp tam giác đều
HĐ 4
a) Vẽ tam giác đều ABC. Hãy trình bày cách xác định tâm đường tròn ngoại tiếp tam giác ABC và vẽ đường tròn đó.
b) Giải thích vì sao tâm O của đường tròn ngoại tiếp tam giác ABC trùng với trọng tâm của tam giác đó (H.9.17)
c) Giải thích vì sao ![]() và
và ![]() (với M là trung điểm của BC) (H.9.17)
(với M là trung điểm của BC) (H.9.17)
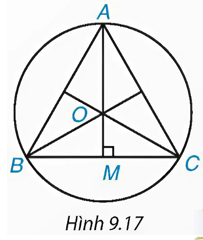
Giải:
a) Tâm đường tròn ngoại tiếp tam giác đều là giao điểm của các đường trung trực và các đường trung trực trong tam giác đều cũng là đường cao, đường trung tuyến, đường phân giác.
b) Vì tam giác ABC đều nên ba đường trung trực cũng đồng thời là ba đường trung tuyến, do đó giao điểm O của ba đường trên là trọng tâm của tam giác.
c) Trong tam giác đều, đường phân giác xuất phát từ một đỉnh trùng với đường trung tuyến xuất phát từ đỉnh đó nên ![]() là phân giác
là phân giác ![]() . Do đó
. Do đó ![]() . Xét
. Xét ![]() vuông tại
vuông tại ![]() có
có ![]()
Do ![]() là trung điểm
là trung điểm ![]() nên
nên ![]()
Suy ra ![]()
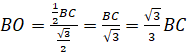
ĐỊNH NGHĨA
------------------------- Còn tiếp -------------------------
II. BÀI TẬP TỰ LUẬN KÌ 2 TOÁN 9 KẾT NỐI TRI THỨC
- Bài tập file word Toán 9 kết nối Bài 18: Hàm số y = ax^2 (a ≠ 0)
- Bài tập file word Toán 9 kết nối Bài 19: Phương trình bậc hai một ẩn
- Bài tập file word Toán 9 kết nối Bài 20: Định lí Viète và ứng dụng
- Bài tập file word Toán 9 kết nối Bài 21: Giải bài toán bằng cách lập phương trình
- Bài tập file word Toán 9 kết nối Bài 22: Bảng tần số và biểu đồ tần số
- Bài tập file word Toán 9 kết nối Bài 23: Bảng tần số tương đối và biểu đồ tần số tương đối
- Bài tập file word Toán 9 kết nối Bài 24: Bảng tần số, tần số tương đối ghép nhóm và biểu đồ
- Bài tập file word Toán 9 kết nối Bài 25: Phép thử ngẫu nhiên và không gian mẫu
- Bài tập file word Toán 9 kết nối Bài 26: Xác suất của biến cố liên quan tới phép thử
- Bài tập file word Toán 9 kết nối Bài 27: Góc nội tiếp
- Bài tập file word Toán 9 kết nối Bài 28: Đường tròn ngoại tiếp và đường tròn nội tiếp của một tam giác
- Bài tập file word Toán 9 kết nối Bài 29: Tứ giác nội tiếp
- Bài tập file word Toán 9 kết nối Bài 30: Đa giác đều
- Bài tập file word Toán 9 kết nối Bài 31: Hình trụ và hình nón
- Bài tập file word Toán 9 kết nối Bài 32: Hình cầu
BÀI 21: GIẢI TOÁN BẰNG CÁCH LẬP PHƯƠNG TRÌNH
(13 CÂU)
1. NHẬN BIẾT (4 CÂU)
Câu 1: Em hãy nêu các bước giải một bài toán bằng cách lập phương trình.
Trả lời
Bước 1. Lập phương trình:
Chọn ẩn số và đặt điều kiện thích hợp cho ẩn số.
Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết.
Lập phương trình biểu thị mối quan hệ giữa các đại lượng.
Bước 2. Giải phương trình.
Bước 3. Trả lời: Kiểm tra xem trong các nghiệm của phương trình, nghiệm nào thoả mãn điều kiện của ẩn, nghiệm nào không, rồi kết luận.
Câu 2: Khi lập phương trình, các đại lượng chưa biết được biểu diễn dựa trên những gì?
Trả lời
Các đại lượng chưa biết được biểu diễn theo ẩn số và các đại lượng đã biết.
Câu 3: Trong lúc học nhóm, bạn Hùng yêu cầu bạn Minh và bạn Lan mỗi người chọn một số sao cho hai số này hơn kém nhau là 5 và tích của chúng phải bằng 150. Vậy hai bạn Minh và Lan phải chọn những số nào?
Trả lời:
Gọi số mà một bạn đã chọn là x và số bạn kia là x + 5
Tích của hai số là x(x + 5)
Theo đầu bài, ta có phương trình x(x + 5)=150 <=>x2 + 5x - 150 = 0 .
Giải phương trình = 25 – 4 . (- 150) = 625 = 252 nên x1 = 10; x2 = - 15
Trả lời: Nếu bạn Minh chọn số 10 thì bạn Lan chọn số 15 hoặc ngược lại.
Nếu bạn minh chọn số – 15 thì bạn Lan chọn số – 10 hoặc ngược lại.
Câu 4: Một hình chữ nhật có chiều dài gấp 3 lần chiều rộng. Nếu cả chiều dài và chiều rộng cùng tăng thêm 5 cm thì được một hình chữ nhật mới có diện tích bằng 153 cm². Tìm chiều dài và chiều rộng của hình chữ nhật ban đầu.
Trả lời:
Gọi x là chiều rộng hình chữ nhật lúc đầu (x > 0) (cm)
Chiều dài hình chữ nhật lúc đầu: 3x (cm)
Chiều rộng hình chữ nhật lúc sau: x + 5 (cm)
Chiều dài hình chữ nhật lúc sau: 3x + 5 (cm)
Theo đề bài ta có phương trình: (x + 5)(3x + 5) = 153
<=> 3x2 + 20x - 128 = 0 <=> x = 4 (thỏa mãn) hay x = - 32/3 < 0(L)
Vậy chiều dài và chiều rộng hình chữ nhật ban đầu là: 12 cm và 4 cm.
Câu 5: Một mảnh đất hình chữ nhật có chiều dài hơn chiều rộng 5 m. Tính kích thước của mảnh đất, biết rằng diện tích mảnh đất là 150 m²
Trả lời:
Gọi chiều rộng của mảnh đất là a (m), a > 0
Khi đó ta có chiều dài của mảnh đất là a + 5(m)
Theo bài ra ta có diện tích của mảnh đất m² nên: a(a - 15) = 150 => a = 10(tm) ; a = - 15 (loại)
Vậy chiều rộng là 10m, chiều dài là 15 m.
2. THÔNG HIỂU (4 CÂU)
Câu 1: Trong tháng đầu hai tổ công nhân sản xuất được 800 chi tiết máy. Sang tháng thứ hai, tổ 1 sản xuất vượt mức 15%, tổ II sản xuất vượt mức 20%. Do đó cuối tháng cả hai tổ sản xuất được 945 chi tiết máy. Hỏi trong tháng đầu mỗi tổ công nhân sản xuất được bao nhiêu chi tiết máy.
Trả lời:
Gọi x là số chi tiết máy của tổ I sản xuất trong tháng đầu (0<x<800, x∈N)
Số chi tiết máy của tổ II sản xuất trong tháng đầu là: 800 – x (chi tiết).
Số chi tiết máy tổ 1 vượt mức ở tháng thứ hai là: ![]() x (chi tiết)
x (chi tiết)
Số chi tiết máy tổ II vượt mức ở tháng thứ hai là: ![]() (800-x) (chi tiết)
(800-x) (chi tiết)
Số chi tiết máy cả hai tổ vượt mức trong tháng thứ hai là: 945-800=145 (chi tiết)
Ta có phương trình: ![]() x +
x + ![]() (800-x) = 145
(800-x) = 145
15x – 20x + 16000 <=> x = 300 (nhận)
Vậy trong tháng đầu tổ 1 sản xuất được 300 chi tiết máy; Tổ II sản xuất được 800-300 = 500 chi tiết máy.
Câu 2: Một đội xe cần chở 12 tấn hàng. Khi làm việc, do 2 xe cần điều đi nơi khác. Nên mỗi xe phải chở thêm 16 tấn hàng. Hỏi lúc đầu đội có bao nhiêu xe?
Trả lời:
Gọi số xe của đội lúc đầu là x(xe) (xe ![]() N, x>12)
N, x>12)
Theo dự định mỗi xe phải chở ![]() (tấn hàng)
(tấn hàng)
Số xe trên thực tế là: x - 2 (xe).
Thực tế mỗi xe phải chở: ![]() (tấn hàng)
(tấn hàng)
Ta có phương trình: ![]() -
- ![]() = 16
= 16
<=> 120x – 120(x – 2) = 16x(x – 2) <=> x2 – 2x - 15 = 0
<=> x = 5 (nhận) hoặc x = -3 (loại)
Vậy đội lúc đầu có 5 xe.
Câu 3: Một phân xưởng theo kế hoạch cần phải sản xuất 1100 sản phẩm trong một số ngày quy định. Do mỗi ngày phân xưởng đó sản xuất vượt mức 5 sản phẩm nên phân xưởng đã hoàn thành kế hoạch sớm hơn thời gian quy định 2 ngày. Hỏi theo kế hoạch, mỗi ngày phân xưởng phải sản xuất bao nhiêu sản phẩm?
Trả lời:
Gọi x (sp) là sản phẩm xưởng sản xuất trong 1 ngày theo kế hoạch (x > 0)
Số ngày theo kế hoạch là: ![]()
Số ngày thực tế là: ![]()
Ta có phương trình: ![]() -
- ![]() = 2
= 2
<=> 1100(x + 5) – 1100x = 2x(x + 5) <=> 2x2 + 10x – 5500 = 0
<=> x = 50 (nhận) hoặc x = -55 (loại)
Vậy theo kế hoạch mỗi ngày phân xưởng phải sản xuất là 50 sản phẩm.
Câu 4: Một lâm trường dự định trồng 75 ha rừng trong một số tuần (mỗi tuần trồng được diện tích bằng nhau). Thực tế, mỗi tuần lâm trường trồng vượt mức 5 ha so với dự định nên cuối cùng đã trồng được 80 ha và hoàn thành sớm hơn dự định một tuần. Hỏi mỗi tuần lâm trường dự định trồng bao nhiêu ha rừng?
Trả lời:
Gọi diện tích rừng mà mỗi tuần lâm trường dự định trồng là x(ha) (Điều kiện: x > 0 )
Theo dự định, thời gian trồng hết 75 ha rừng là: ![]() (tuần)
(tuần)
Vì mỗi tuần lâm trường trồng vượt mức 5 ha so với dự định nên thực tế mỗi tuần lâm trường trồng được: x + 5 (ha)
Do đó thời gian thực tế lâm trường trồng hết 80 ha rừng là: 80/(x + 5) (tuần)
Vì thực tế, lâm trường trồng xong sớm so với dự định là 1 tuần nên ta có phương trình:
![]()
<=> 75( x + 5) – 80x = x(x + 5)
<=> x = 15 (nhận) hoặc x = -25 (loại)
Vậy mỗi tuần lâm trường dự định trồng 15 ha rừng.
Câu 5: Quãng đường từ A đến B dài 90 km. Một người đi xe máy từ A đến B. Khi đến B, người đó nghỉ 30 phút rồi quay trở về A với vận tốc lớn hơn vận tốc lúc đi là 9 km/h. Thời gian kể từ lúc bắt đầu đi từ A đến lúc trở về đến A là 5 giờ. Tính vận tốc xe máy lúc đi từ A đến B.
Trả lời:
Đặt x (km/h) là vận tốc đi từ A đến B, vậy vận tốc đi từ B đến A là x + 9 (km/h)
Do giả thiết ta có:
![]()
<=> ![]()
<=> x(x + 9) = 20(2x + 9)
<=> x2 – 31x – 180 = 0
<=> x = 36 (do x > 0)
Vậy vận tốc xe máy lúc đi từ A đến B là 36 km/h
------------------------- Còn tiếp -------------------------
BÀI 29: TỨ GIÁC NỘI TIẾP
(14 CÂU)
2. THÔNG HIỂU (4 CÂU)
Câu 1: Trong hình vẽ dưới đây, cho a = 140 độ
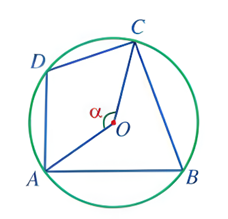
a) Tính các góc ![]() ,
, ![]() của tứ giác ABCD
của tứ giác ABCD
b) Tính ![]() +
+ ![]()
Trả lời:
a) Ta có: ![]() (góc nội tiếp và góc ở tâm cùng chắn cung AC)
(góc nội tiếp và góc ở tâm cùng chắn cung AC)
![]() +
+ ![]() =
= ![]() (tứ giác ABCD nội tiếp đường tròn)
(tứ giác ABCD nội tiếp đường tròn)
![]() +
+ ![]() =
= ![]()
![]() =
= ![]() -
- ![]()
![]() =
= ![]()
b) Tứ giác ABCD nội tiếp đường trong nên ![]() +
+ ![]() =
= ![]()
Câu 2: Cho tứ giác ABCD nội tiếp đường tròn. Tính số đo các góc còn lại của tứ giác đó trong trường hợp sau: ![]() = 45
= 45![]() và
và ![]() = 155
= 155![]()
Trả lời:
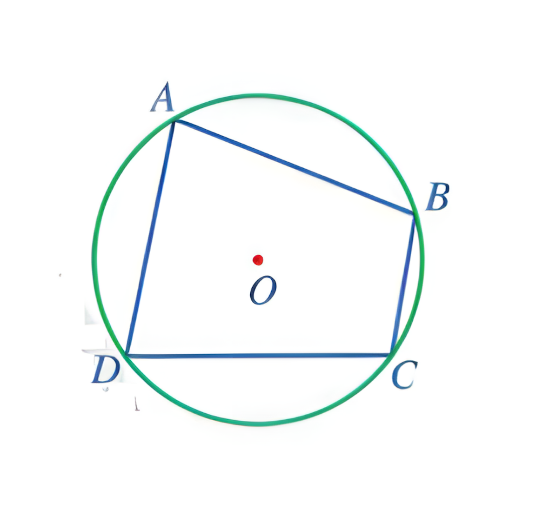
Ta có: ![]() (tứ giác
(tứ giác ![]() nội tiếp đường tròn )
nội tiếp đường tròn )
![]()
Ta có: ![]() (tứ giác
(tứ giác ![]() nội tiếp đường tròn )
nội tiếp đường tròn )
![]()
Câu 3: Trong hình vẽ dưới đây, cho ADC = 40 độ, BCD = 100 độ
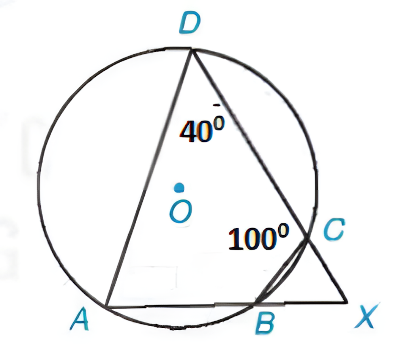
a) Tính các góc ![]() ,
, ![]() của tứ giác ABCD
của tứ giác ABCD
b) Tính ![]()
Trả lời:
a) Ta có:
b) Ta có:
![]()
Câu 4: Cho tam giác ABC có ba góc nhọn. Vẽ các đường cao BD và CE của tam giác ABC . Gọi H là giao điểm của BD và CE. Chứng minh ADHE là tứ giác nội tiếp
Trả lời:
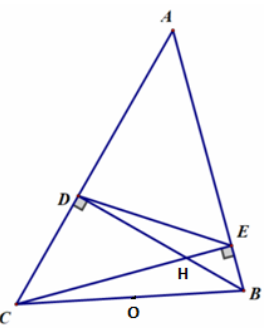
Vì BD, CE là các đường cao của tam giác ABC nên ![]()
 =
=  = 90 độ
= 90 độ
Xét tứ giác ADHE có ![]() +
+ ![]() = 90
= 90![]() + 90
+ 90![]() = 180
= 180![]()
=> ADHE là tứ giác nội tiếp (tứ giác có tổng 2 góc đối bằng 180![]() )
)
3. VẬN DỤNG (2 CÂU)
Câu 1: Cho nửa đường tròn đường kính AD. Lấy điểm B thuộc nửa đường tròn (B khác A và D), trên cung BD lấy điểm C (C khác B và D). Hai dây AC, BD cắt nhau tại điểm E. Kẻ đoạn thẳng EF vuông góc với AD (F∈ AD):
a) Chứng minh tứ giác ABEF nội tiếp
b) Chứng minh AE.AC = AF.AD.
Trả lời:
Ta có hình vẽ:
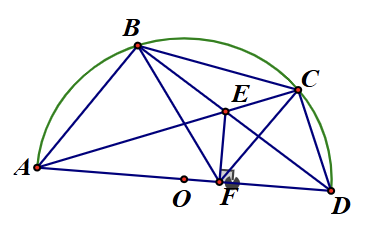
a) Chứng minh tứ giác ABEF nội tiếp
B thuộc (O) ⇒ ![]() = 90° (góc nội tiếp chắn nửa đường tròn ) ⇒
= 90° (góc nội tiếp chắn nửa đường tròn ) ⇒ ![]() = 90° EF
= 90° EF![]() AD (gt) ⇒
AD (gt) ⇒ ![]() = 90°
= 90°
Xét tứ giác ABEF có ![]() mà 2 góc này đối nhau
mà 2 góc này đối nhau
⇒ABEF là tứ giác nội tiếp
b) Chứng minh AE.AC = AF.AD :
Có C ∈ (O) ⇒![]() = 90° (góc nội tiếp chắn nửa đường tròn)
= 90° (góc nội tiếp chắn nửa đường tròn)
Xét ∆AFE và ∆ACD có:![]() chung,
chung, ![]()
⇒ ∆AFE ![]() ∆ACD (g . g) ⇒
∆ACD (g . g) ⇒ ![]() AE.AC = AF.AD (đpcm).
AE.AC = AF.AD (đpcm).
Câu 2: Cho tam giác nhọn ![]() . Đường tròn
. Đường tròn ![]() đường kính
đường kính ![]() cắt
cắt ![]() lần lượt tại
lần lượt tại ![]() . Đường thẳng
. Đường thẳng ![]() cắt
cắt ![]() tại
tại ![]() và đường thẳng
và đường thẳng ![]() cắt
cắt ![]() tại
tại ![]() .
.
a) Chứng minh tứ giác ![]() nội tiếp.
nội tiếp.
b) Chứng minh tứ giác ![]() nội tiếp.
nội tiếp.
Trả lời:
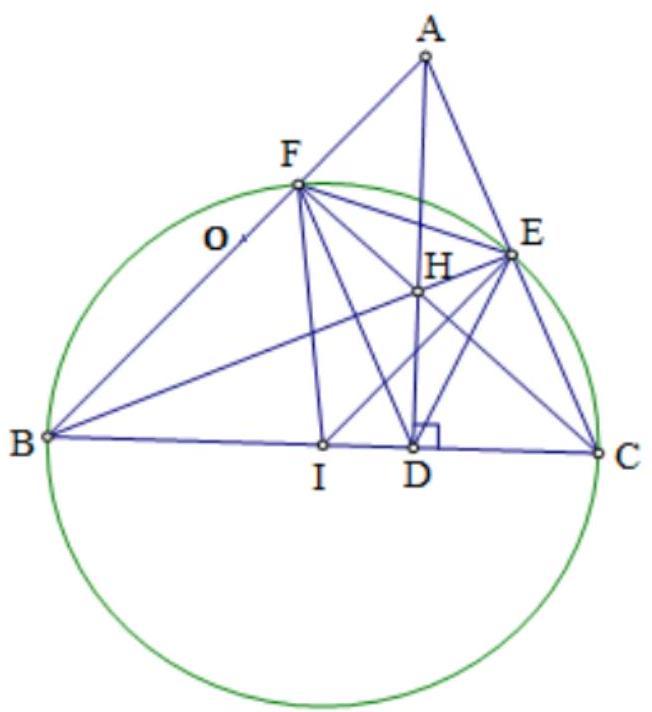
a) Chứng minh tứ giác ![]() nội tiếp.
nội tiếp.
- Xét đường tròn ![]() có:
có:![]() (góc nội tiếp chắn nửa đường tròn)
(góc nội tiếp chắn nửa đường tròn) ![]()
![]() (góc nội tiếp chắn nửa đường tròn)
(góc nội tiếp chắn nửa đường tròn) ![]()
Suy ra ![]() là trực tâm của tam giác
là trực tâm của tam giác ![]() hay
hay ![]()
- Xét tứ giác ![]() có:
có:
![]()
tứ giác ![]() có tổng hai góc đối
có tổng hai góc đối ![]() bằng
bằng ![]() nên tứ giác
nên tứ giác ![]() nội tiếp.
nội tiếp.
b) Chứng minh tứ giác ![]() nội tiếp.
nội tiếp.
Gọi ![]() là trung điểm
là trung điểm ![]() .
.
Xét tam giác ![]() có
có ![]() và
và ![]() là đường trung tuyến nên
là đường trung tuyến nên ![]()
------------------------- Còn tiếp -------------------------

Đủ kho tài liệu môn học
=> Tài liệu sẽ được gửi ngay và luôn
Cách tải:
- Bước 1: Chuyển phí vào STK: 1214136868686 - cty Fidutech - MB
- Bước 2: Nhắn tin tới Zalo Fidutech - nhấn vào đây để thông báo và nhận tài liệu
=> Giáo án toán 9 kết nối tri thức
Từ khóa: giáo án điện tử kì 2 Toán 9 kết nối tri thức, giáo án Toán 9 kết nối tri thức, ppt Toán 9 kết nối tri thức