Giáo án điện tử chuyên đề Toán 11 kết nối Bài tập cuối CĐ 1

CHÀO MỪNG CÁC EM 

ĐẾN VỚI TIẾT HỌC

HÔM NAY!

KHỞI ĐỘNG

Mặt phẳng tọa độ, phép tịnh tiến theo vectơ biến đường thẳng thành đường thẳng có phương trình

                   A.                           B.

                   C.                           D.

Giải

Phép tịnh tiến theo vectơ biến điểm thành điểm thì: 

Thay vào phương trình được:

hay

Đáp án cần chọn là B.

CHUYÊN ĐỀ 1: PHÉP BIẾN HÌNH TRONG MẶT PHẲNG

BÀI TẬP CUỐI CHUYÊN ĐỀ 1 

ÔN TẬP 

CUỐI CHUYÊN ĐỀ 1

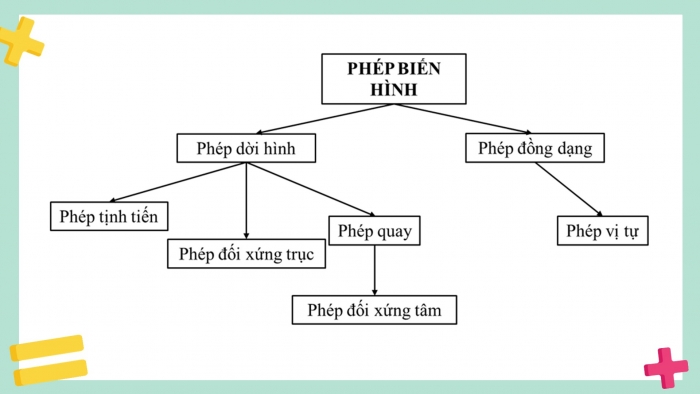
- Phép dời hình (chẳng hạn phép tịnh tiến, phép đối xứng trục, phép quay và phép đối xứng tâm) bảo toàn khoảng cách giữa hai điểm bất kì; biến đường thẳng thành đường thẳng, biến tia thành tia, biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn có cùng bán kính và có tâm là ảnh của tâm.

- Phép đồng dạng (chẳng hạn phép vị tự hoặc thực hiện liên tiếp một phép dời hình và một phép vị tự) biến đường thẳng thành đường thẳng, biến tia thành tia, biến tam giác thành tam giác đồng dạng với nó, biến đường tròn thành đường tròn với tâm là ảnh của tâm.

HOẠT ĐỘNG 

LUYỆN TẬP

Bài 1.27 (SGK-tr33) Trong mặt phẳng toạ độ , cho đường thẳng và hai điểm

a) Tìm toạ độ điểm là ảnh của điểm qua phép đối xứng trục .

b) Xác định điểm thuộc đường thẳng sao cho đạt giá trị nhỏ nhất.

Giải

a) Phép đối xứng trục biến điểm thành điểm .

b) ta có : và

nên hai điểm nằm về một phía của đường thẳng .

Vì và và đối xứng nhau qua nên và và nằm về hai phía của đường thẳng .

Do đó, đạt giá trị nhỏ nhất khi là giao của và .

Có : , suy ra là một vectơ pháp tuyến của đường thẳng  

Phương trình đường thẳng là hay

Tọa độ giao điểm của và là nghiệm của hệ phương trình 

Bài 1.28 (SGK-tr33) Trong mặt phẳng toạ độ , cho đường thẳng . Viết phương trình đường thẳng là ảnh của đường thẳng qua phép tịnh tiến theo vectơ

Gọi thuộc và là ảnh của điểm qua phép tịnh tiến theo vectơ .

Khi đó

Ta có  

Do đó thuộc đường thẳng có phương trình

Vì là ảnh của qua phép tịnh tiến theo vectơ nên thuộc .

Vậy phương trình đường thẳng là .

Bài 1.29 (SGK-tr33) Trong mặt phẳng toạ độ , cho đường tròn . Viết phương trình của đường tròn là ảnh của đường tròn qua phép đối xứng tâm

Giải

Ta có đường tròn có tâm và bán kính

Gọi và lần lượt là tâm và bán kính của đường tròn . Vì là ảnh của qua phép đối xứng tâm nên là ảnh của qua phép đối xứng tâm và

Vì là ảnh của qua phép đối xứng tâm nên là trung điểm của .

Vậy phương trình đường tròn là : .

Bài 1.30 (SGK-tr33) Trong mặt phẳng toạ độ , cho đường tròn . Phép vị tự tâm với tỉ số biến đường tròn thành đường tròn Viết phương trình đường tròn

Ta có Tâm và bán kính

Gọi và lần lượt là tâm và bán kính của . Vì là ảnh của qua phép vị tự tâm với tỉ số nên là ảnh của qua phép vị tự tâm với tỉ số và .

Vì là ảnh của qua phép vị tự nên .

Suy ra

Vậy phương trình đường tròn là: .

HOẠT ĐỘNG 

VẬN DỤNG

Bài 1.31 (SGK-tr33) Cho đường thẳng và hai điểm cùng thuộc một nửa mặt phẳng bờ . Hai điểm thay đổi trên sao cho không đổi. Xác định vị trí của hai điểm để nhỏ nhất.

Giải

Qua phép tịnh tiến theo vectơ điểm biến thành thì cố định và

.

Gọi là điểm đối xứng của qua thì

Dấu xảy ra khi thẳng hàng, tức là trùng với giao điểm của và .

Khi đó điểm là ảnh của qua phép tịnh tiến theo vectơ .

Bài 1.32 (SGK-tr33) Cho tam giác ABC nội tiếp đường tròn tâm O. Các đỉnh B, C cố định còn đỉnh A thay đổi trên đường tròn đó. Vẽ hình bình hành ABCD. Chứng minh rằng điểm D luôn thuộc một đường tròn cố định.

Giải

Vì là hình bình hành nên

Do cố định nên vectơ cố định.

Khi đó ta có phép tịnh tiến theo vectơ biến điểm thành điểm . Mặt khác, thuộc đường tròn tâm ngoại tiếp

thuộc đường tròn tâm có định là ảnh của đường tròn tâm qua phép tịnh tiến theo vectơ .

--------------- Còn tiếp ---------------