Giáo án điện tử chuyên đề Toán 11 kết nối Bài tập cuối CĐ 2
Tải giáo án điện tử Chuyên đề học tập Toán 11 kết nối tri thức Bài tập cuối CĐ 2. Bộ giáo án chuyên đề được thiết kế sinh động, đẹp mắt. Thao tác tải về đơn giản, dễ dàng sử dụng và chỉnh sửa. Thầy, cô kéo xuống để xem chi tiết.
Xem: => Giáo án toán 11 kết nối tri thức
Xem toàn bộ: Giáo án điện tử chuyên đề toán 11 kết nối tri thức
CHÀO MỪNG
TẤT CẢ CÁC EM
ĐẾN VỚI TIẾT HỌC!
KHỞI ĐỘNG
Trình bày khái niệm: Đường đi Euler và Đường đi Hamilton?
CHUYÊN ĐỀ 2: LÀM QUEN VỚI
MỘT VÀI KHÁI NIỆM CỦA
LÍ THUYẾT ĐỒ THỊ
BÀI TẬP CUỐI CHUYÊN ĐỀ 2
HOẠT ĐỘNG
LUYỆN TẬP
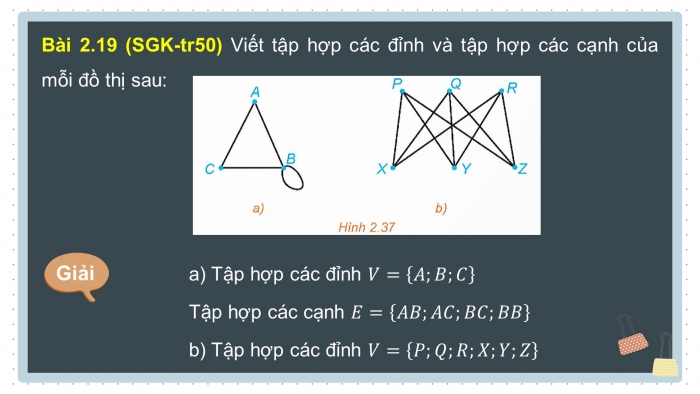
Bài 2.19 (SGK-tr50) Viết tập hợp các đỉnh và tập hợp các cạnh của mỗi đồ thị sau:
Giải
a) Tập hợp các đỉnh 
Tập hợp các cạnh 
b) Tập hợp các đỉnh 
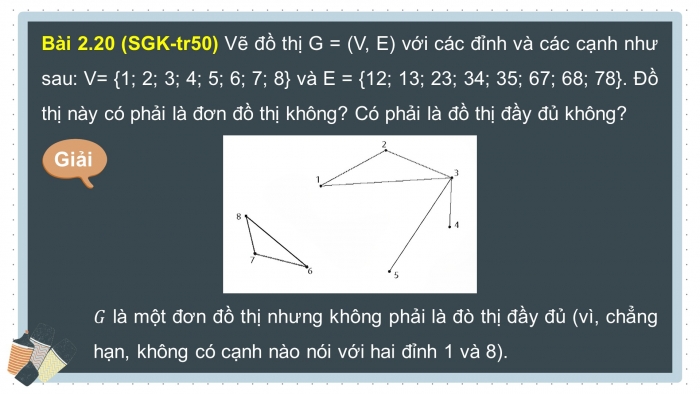
Bài 2.20 (SGK-tr50) Vẽ đồ thị G = (V, E) với các đỉnh và các cạnh như sau: V= {1; 2; 3; 4; 5; 6; 7; 8} và E = {12; 13; 23; 34; 35; 67; 68; 78}. Đồ thị này có phải là đơn đồ thị không? Có phải là đồ thị đầy đủ không?
Giải
là một đơn đồ thị nhưng không phải là đò thị đầy đủ (vì, chẳng hạn, không có cạnh nào nói với hai đỉnh 1 và 8).
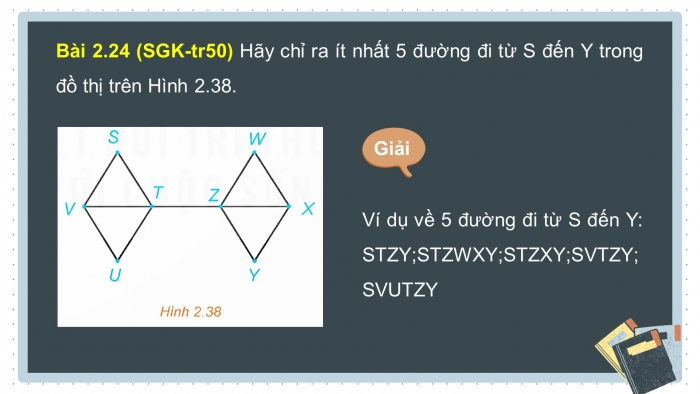
Bài 2.24 (SGK-tr50) Hãy chỉ ra ít nhất 5 đường đi từ S đến Y trong đồ thị trên Hình 2.38.
Giải
Ví dụ về 5 đường đi từ S đến Y: STZY;STZWXY;STZXY;SVTZY;SVUTZY
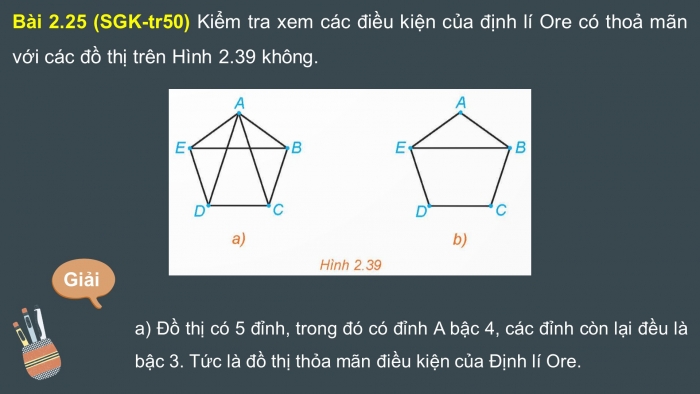
Bài 2.25 (SGK-tr50) Kiểm tra xem các điều kiện của định lí Ore có thoả mãn với các đồ thị trên Hình 2.39 không.
Giải
a) Đồ thị có 5 đỉnh, trong đó có đỉnh A bậc 4, các đỉnh còn lại đều là bậc 3. Tức là đồ thị thỏa mãn điều kiện của Định lí Ore.
b) Đồ thị có 5 đỉnh, trong đó có hai đỉnh B,E bậc 3, các đỉnh còn lại đều là bậc 2. Tức là đồ thị không thỏa mãn điều kiện của định lí Ore.
Bài 2.26 (SGK-tr51) Tìm một chu trình Euler trong đồ thị trên Hình 2.40.
Giải
Một chu trình Euler cần tìm là 
.
HOẠT ĐỘNG
VẬN DỤNG
Bài 2.21 (SGK-tr50) Chứng minh rằng không có đơn đồ thị với 12 đỉnh và 28 cạnh mà các đỉnh đều có bậc 3 hoặc 6.
Giải
Gọi 
là số đỉnh bậc 3 của đồ thị
Khi đó số đỉnh bậc 6 của đồ thị là: 
Tổng số bậc của các đỉnh là: 
Do đồ thị có 28 cạnh nên ta có: 
Do đồ thị có 28 cạnh nên ta có: 
, tức là 
. Phương trình này không có nghiệm là số tự nhiên. Do đó, không tồn tại đồ thị thỏa mãn điều kiện đề bài.
Bài 2.22 (SGK-tr50) Chứng minh rằng nếu G là một đơn đồ thị có ít nhất hai đỉnh thì G có ít nhất hai đỉnh có cùng bậc.
Giải
Giả sử 
là một đơn đồ thị với 
đỉnh 
Vì 
là một đơn đồ thị nên mỗi đỉnh được nối với tối đa 
đỉnh khác (do hai đỉnh chỉ được nối với nhau bằng nhiều nhất một cạnh).
Do đó, mỗi đỉnh có số bậc tối đa là 
Ta thấy 
có 
đỉnh, mà có 
loại bậc, nên tồn tại ít nhất hai đỉnh có cùng bậc với nhau.
--------------- Còn tiếp ---------------
Trên chỉ là 1 phần của giáo án. Giáo án khi tải về có đầy đủ nội dung của bài. Đủ nội dung của học kì I + học kì II
Hệ thống có đủ tài liệu:
- Giáo án điện tử chuyên đề toán 11 kết nối tri thức (350k)
- Giáo án toán 11 kết nối tri thức (300k)
- Giáo án powerpoint toán 11 kết nối tri thức (350k)
- Giáo án dạy thêm toán 11 kết nối tri thức (300k)
- Giáo án chuyên đề toán 11 kết nối tri thức (300k)
- Câu hỏi và bài tập trắc nghiệm toán 11 kết nối tri thức (150k)
- Đề thi toán 11 kết nối tri thức (200k)
- File bài tập toán 11 Kết nối tri thức (150k)
- File word đáp án toán 11 kết nối tri thức (100k)
- Bài tập file word Toán 11 kết nối tri thức (150k)
- Kiến thức trọng tâm Toán 11 kết nối tri thức (150k)
- Đề kiểm tra 15 phút Toán 11 kết nối tri thức (100k)
- Giáo án powerpoint chuyên đề toán 11 kết nối tri thức (350k)
- Phiếu học tập theo bài Toán 11 kết nối tri thức cả năm (150k)
- Trắc nghiệm đúng sai Toán 11 kết nối tri thức cả năm (150k)
- Trắc nghiệm dạng câu trả lời ngắn Toán 11 kết nối tri thức cả năm (150k)
=> Có thể chọn nâng cấp VIP với phí là 1050k để tải tất cả tài liệu ở trên
- Chỉ gửi 500k. Tải về dùng thực tế, 1 ngày sau mới gửi số còn lại.
Cách tải hoặc nâng cấp:
- Bước 1: Chuyển phí vào STK: 1214136868686 - cty Fidutech - MB
- Bước 2: Nhắn tin tới Zalo Fidutech - nhấn vào đây để thông báo và nhận tài liệu
Xem toàn bộ: Giáo án điện tử chuyên đề toán 11 kết nối tri thức
ĐẦY ĐỦ GIÁO ÁN CÁC BỘ SÁCH KHÁC
GIÁO ÁN WORD LỚP 11 KẾT NỐI TRI THỨC
GIÁO ÁN POWERPOINT LỚP 11 KẾT NỐI TRI THỨC
GIÁO ÁN CHUYÊN ĐỀ LỚP 11 KẾT NỐI TRI THỨC
GIÁO ÁN DẠY THÊM 11 KẾT NỐI TRI THỨC
CÁCH ĐẶT MUA:
Liên hệ Zalo: Fidutech - nhấn vào đây