Giáo án powerpoint dạy thêm Toán 8 chân trời Bài: Bài tập cuối chương 3
Tải giáo án Powerpoint dạy thêm Toán 8 chân trời sáng tạo Chương 3 Bài tập cuối chương 3. Giáo án điện tử thiết kế hiện đại, đẹp mắt, nhiều bài tập ôn tập, mở rộng kiến thức phong phú. Tài liệu tài về và chỉnh sửa được. Mời thầy cô và các bạn kéo xuống theo dõi.
Xem: => Giáo án toán 8 chân trời sáng tạo
Click vào ảnh dưới đây để xem 1 phần giáo án rõ nét



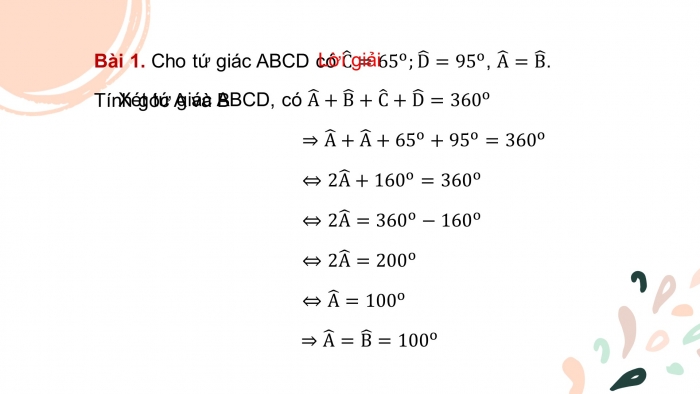
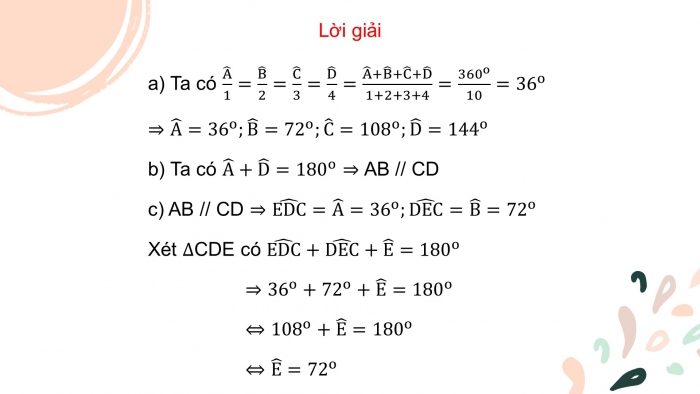

Các tài liệu bổ trợ khác
Xem toàn bộ: Giáo án powerpoint dạy thêm toán 8 chân trời sáng tạo đủ cả năm
NHIỆT LIỆT CHÀO MỪNG
CÁC EM HỌC SINH
THAM DỰ BUỔI HỌC HÔM NAY
BÀI TẬP CUỐI CHƯƠNG 3
PHIẾU BÀI TẬP SỐ 1
Bài 1. Cho tứ giác ABCD có C ̂=〖65〗^o;D ̂=〖95〗^o, A ̂=B ̂.
Tính góc A và B
Lời giải
Xét tứ giác ABCD, có A ̂+B ̂+C ̂+D ̂=〖360〗^o
⇒A ̂+A ̂+〖65〗^o+〖95〗^o=〖360〗^o
⇔2A ̂+〖160〗^o=〖360〗^o
⇔2A ̂=〖360〗^o-〖160〗^o
⇔2A ̂=〖200〗^o
⇔A ̂=〖100〗^o
⇒A ̂=B ̂=〖100〗^o
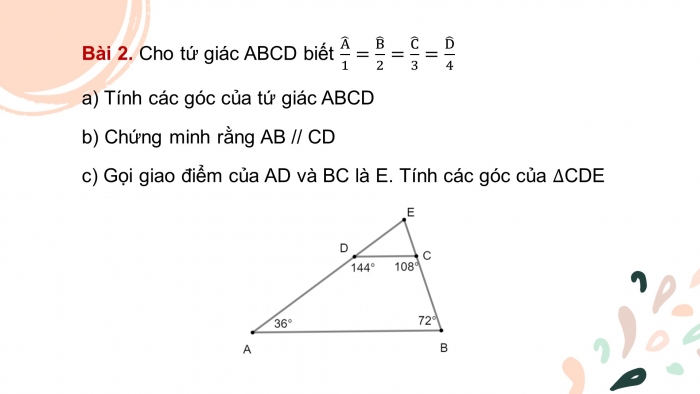
Bài 2. Cho tứ giác ABCD biết A ̂/1=B ̂/2=C ̂/3=D ̂/4
- a) Tính các góc của tứ giác ABCD
- b) Chứng minh rằng AB // CD
- c) Gọi giao điểm của AD và BC là E. Tính các góc của ∆CDE
Lời giải
- a) Ta có A ̂/1=B ̂/2=C ̂/3=D ̂/4=(A ̂+B ̂+C ̂+D ̂)/(1+2+3+4)=〖360〗^o/10=〖36〗^o
⇒A ̂=〖36〗^o;B ̂=〖72〗^o;C ̂=〖108〗^o;D ̂=〖144〗^o
- b) Ta có A ̂+D ̂=〖180〗^o⇒ AB // CD
- c) AB // CD ⇒(EDC) ̂=A ̂=〖36〗^o;(DEC) ̂=B ̂=〖72〗^o
Xét ∆CDE có (EDC) ̂+(DEC) ̂+E ̂=〖180〗^o
⇒〖36〗^o+〖72〗^o+E ̂=〖180〗^o
⇔〖108〗^o+E ̂=〖180〗^o
⇔E ̂=〖72〗^o
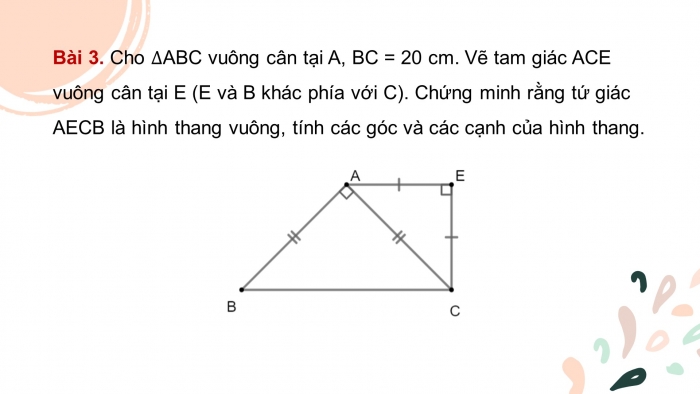
Bài 3. Cho ∆ABC vuông cân tại A, BC = 20 cm. Vẽ tam giác ACE vuông cân tại E (E và B khác phía với C). Chứng minh rằng tứ giác AECB là hình thang vuông, tính các góc và các cạnh của hình thang.
Lời giải
∆ABC vuông cân tại A ⇒(ACB) ̂=〖45〗^o
∆AEC vuông cân tại E ⇒(EAC) ̂=〖45〗^o
⇒(ACB) ̂=(EAC) ̂=〖45〗^o
Mà hai góc ở vị trí so le trong
⇒ AE // BC ⇒ AECB là hình thang
Lại có (AEC) ̂=〖90〗^o⇒ AECB là hình thang vuông
Đặt AB = AC = x ⇒2x^2=4⇔x=√2 cm
Đặt AE = EC = y ⇒2y^2=2⇔y=1 cm
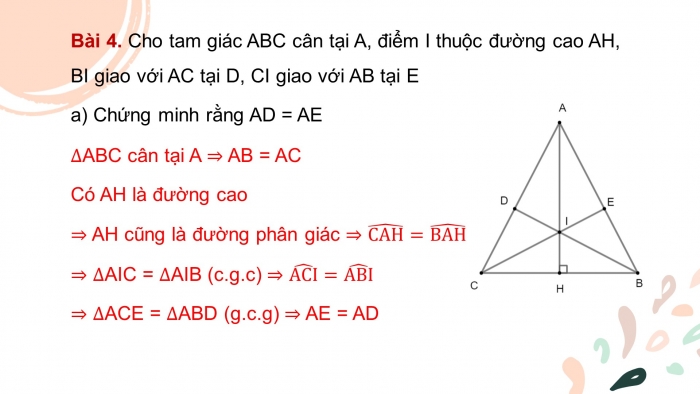
Bài 4. Cho tam giác ABC cân tại A, điểm I thuộc đường cao AH, BI giao với AC tại D, CI giao với AB tại E
- a) Chứng minh rằng AD = AE
∆ABC cân tại A ⇒ AB = AC
Có AH là đường cao
⇒ AH cũng là đường phân giác ⇒(CAH) ̂=(BAH) ̂
⇒∆AIC = ∆AIB (c.g.c) ⇒(ACI) ̂=(ABI) ̂
⇒∆ACE = ∆ABD (g.c.g) ⇒ AE = AD
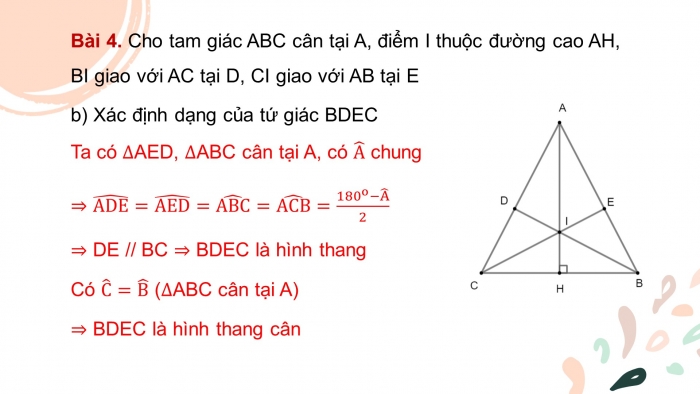
- b) Xác định dạng của tứ giác BDEC
Ta có ∆AED, ∆ABC cân tại A, có A ̂ chung
⇒(ADE) ̂=(AED) ̂=(ABC) ̂=(ACB) ̂=(〖180〗^o-A ̂)/2
⇒ DE // BC ⇒ BDEC là hình thang
Có C ̂=B ̂ (∆ABC cân tại A)
⇒ BDEC là hình thang cân
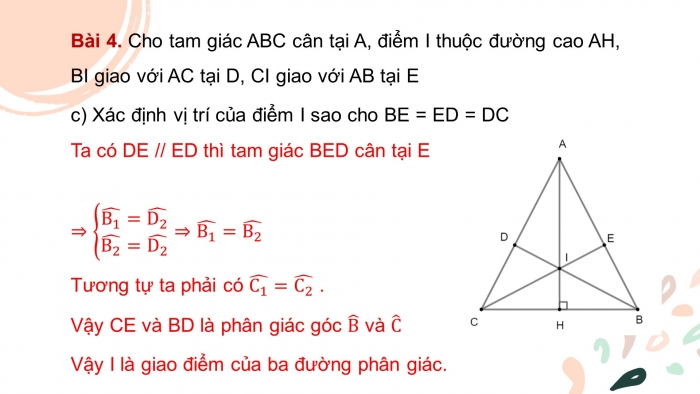
- c) Xác định vị trí của điểm I sao cho BE = ED = DC
Ta có DE // ED thì tam giác BED cân tại E
⇒ {█((B_1 ) ̂=(D_2 ) ̂@(B_2 ) ̂=(D_2 ) ̂ )┤⇒(B_1 ) ̂=(B_2 ) ̂
Tương tự ta phải có (C_1 ) ̂=(C_2 ) ̂ .
Vậy CE và BD là phân giác góc B ̂ và C ̂
Vậy I là giao điểm của ba đường phân giác.
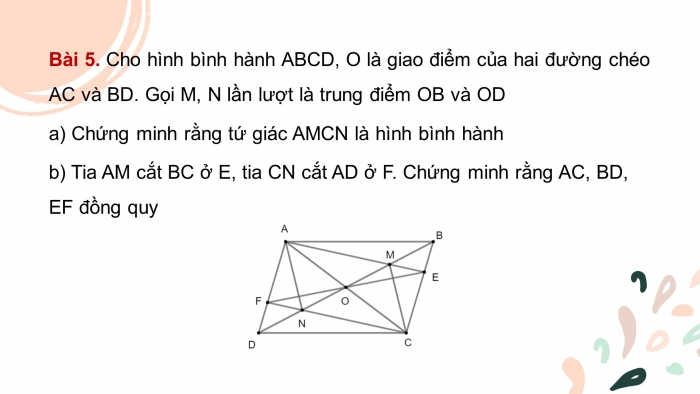
Bài 5. Cho hình bình hành ABCD, O là giao điểm của hai đường chéo AC và BD. Gọi M, N lần lượt là trung điểm OB và OD
- a) Chứng minh rằng tứ giác AMCN là hình bình hành
- b) Tia AM cắt BC ở E, tia CN cắt AD ở F. Chứng minh rằng AC, BD, EF đồng quy
Lời giải
- a) ABCD là hình bình hành
⇒ OA = OC; OB = OD
có M, N là trung điểm của OB, OD
⇒ ON = OM
Xét tứ giác AMCN có OA = OC; ON = OM
⇒ AMCN là hình bình hành
- b) Ta có AMCN là hình bình hành ⇒ AM // CN
mà AM cắt BC tại E ⇒ A, M , E thẳng hàng
CN cắt AD tại F ⇒ A, N, F thẳng hàng
⇒ AE // CF (1)
Mặt khác ABCD là hình bình hành ⇒ AD // BC ⇒ AF // EC (2)
Từ (1) và (2) suy ra AECF là hình bình hành ⇒ AC và EF cắt nhau tại O
Mà AC và BD cắt nhau tại O (ABCD là hình bình hành)
⇒ AC, BD, EF đồng quy
Bài 6. Cho hình bình hành ABCD có AC vuông góc AD. Gọi E, F theo thứ tự là trung điểm của các cạnh AB, CD. Chứng minh tứ giác AECF là hình thoi.
Lời giải
Ta có ABCD là hình bình hành ⇒ AB // DC; AB = DC
Mà E, F là trung điểm của AB, DC ⇒ AE = BE; DF = CF
⇒ AE // DF, AE = DF ⇒ AEFD là hình bình hành ⇒ EF // AD
Lại có AC ⊥ AD
⇒ AC ⊥ EF
⇒ AECF là hình thoi
Bài 7. Cho tam giác ABC cân tại A, các đường trung tuyến BD, CE cắt nhau tại O. Gọi M là điểm đối xứng của O qua D và N là
điểm đối xứng của O qua E. Tứ giác BNMC là hình gì? Vì sao?
Lời giải
Ta có M là điểm đối xứng với O qua D nên OD = DM
O là trọng tâm của ∆ABC nên BO = 2OD ⇒ BO = OM
Tương tự ta có CO = ON
Tứ giác BNMC có OD = DM; CO = ON
Mà NC và BM là hai đường chéo
⇒ BNMC là hình bình hành
Có ∆BDC = ∆CEB (c.g.c) ⇒(B_1 ) ̂=(C_1 ) ̂⇒ BO = CO ⇒ BM = CN
⇒ BNMC là hình chữ nhật
Bài 8. Cho hình vuông ABCD. Trên cạnh AD, DC lần lượt lấy các điểm E, F sao cho AE = DF. Chứng minh
- a) Hai tam giác ADF và BAE bằng nhau;
- b) BE vuông góc với AF.
Lời giải
- a) Vì ABCD là hình vuông nên AB = AD và D ̂=(EAB) ̂=〖90〗^o
Xét ∆ADF và ∆BAE ta có:
AD = AB
D ̂=(EAB) ̂=〖90〗^o
AE = DF (gt)
Do đó: ΔADF = ΔBAE (c – g – c)
- b) Gọi giao điểm của BE và AF là G.
Ta có: (DFA) ̂+(DAF) ̂=〖90〗^o
Mà (DFA) ̂=(AEB) ̂
(hai góc tương ứng của hai tam giác bằng nhau ΔADF = ΔBAE)
Nên (AEB) ̂+(DAF) ̂=〖90〗^o hay (AEG) ̂+(EAG) ̂=〖90〗^o
Mà theo định lý tổng ba góc trong tam giác AEG ta có:
(AGE) ̂+(AEG) ̂+(EAG) ̂=〖180〗^o ⇒ (AGE) ̂+〖90〗^o=〖180〗^o
⇒ (AGE) ̂=〖90〗^o⇒ BE ⊥ AF tại G
PHIẾU BÀI TẬP SỐ 2
Bài 1. Cho tứ giác lồi ABCD, biết A ̂=D ̂=〖90〗^o, góc B và C khác nhau
- a) Chứng minh AB // DC
...
Trên chỉ là 1 phần của giáo án. Giáo án khi tải về có đầy đủ nội dung của bài. Đủ nội dung của học kì I + học kì II
Đủ kho tài liệu môn học
=> Tài liệu sẽ được gửi ngay và luôn
Cách tải:
- Bước 1: Chuyển phí vào STK: 1214136868686 - cty Fidutech - MB
- Bước 2: Nhắn tin tới Zalo Fidutech - nhấn vào đây để thông báo và nhận tài liệu
Xem toàn bộ: Giáo án powerpoint dạy thêm toán 8 chân trời sáng tạo đủ cả năm
ĐẦY ĐỦ GIÁO ÁN CÁC BỘ SÁCH KHÁC
GIÁO ÁN WORD LỚP 8 CHÂN TRỜI SÁNG TẠO
GIÁO ÁN POWERPOINT LỚP 8 CHÂN TRỜI SÁNG TẠO
GIÁO ÁN DẠY THÊM LỚP 8 CHÂN TRỜI SÁNG TẠO
CÁCH ĐẶT MUA:
Liên hệ Zalo: Fidutech - nhấn vào đây
