Giáo án điện tử chuyên đề Toán 11 chân trời Bài 2: Đường đi Euler và đường đi Hamilton
Tải giáo án điện tử Chuyên đề học tập Toán 11 chân trời sáng tạo Bài 2: Đường đi Euler và đường đi Hamilton. Bộ giáo án chuyên đề được thiết kế sinh động, đẹp mắt. Thao tác tải về đơn giản, dễ dàng sử dụng và chỉnh sửa. Thầy, cô kéo xuống để xem chi tiết.
Xem: => Giáo án toán 11 chân trời sáng tạo
Xem toàn bộ: Giáo án điện tử chuyên đề Toán 11 chân trời sáng tạo
CHÀO MỪNG CÁC EM
ĐẾN VỚI TIẾT HỌC!
KHỞI ĐỘNG
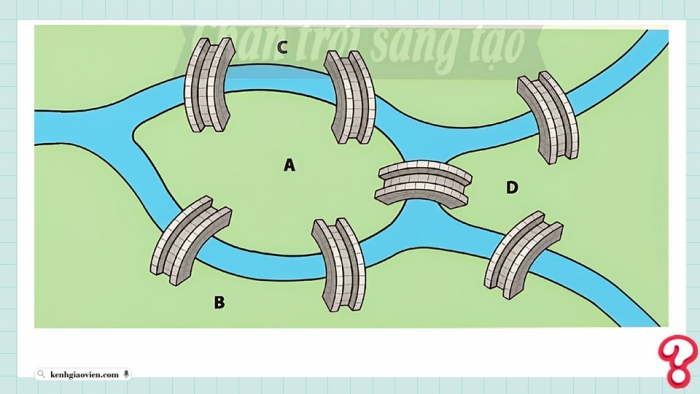
Thành phố Königsberg thuộc Phổ (nay là kaliningrad thuộc Nga) có bảy cây cầu nối bốn vùng đất được chia bởi các nhánh sông Pregel như ở hình dưới.
Vào mỗi sáng Chủ Nhật, người dân thành phố thường đi dạo qua các câu cầu. Họ tự hỏi không biết có thể bắt đầu từ một điểm nào đó trong thành phố, đi qua khắp các cây cầu, mỗi cầu chỉ đi qua một lần, rồi quay về điểm xuất phát.
Theo em, có hay không một cách đi như vậy?
CHUYÊN ĐỀ 2:
LÍ THUYẾT ĐỒ THỊ
BÀI 2: ĐƯỜNG ĐI EULER VÀ ĐƯỜNG ĐI HAMILTON
NỘI DUNG BÀI HỌC
...........................................
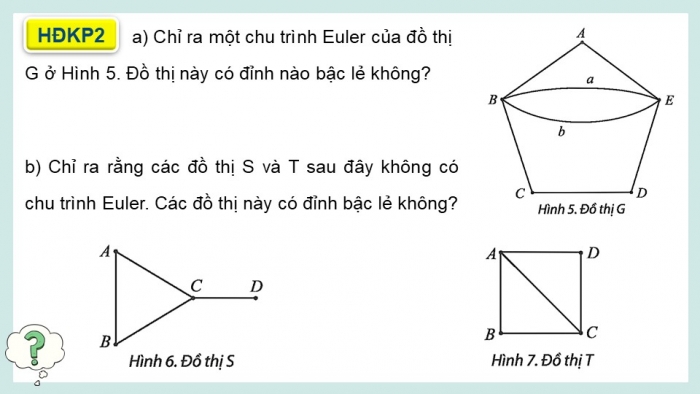
HĐKP2
a) Chỉ ra một chu trình Euler của đồ thị G ở Hình 5. Đồ thị này có đỉnh nào bậc lẻ không?
b) Chỉ ra rằng các đồ thị S và T sau đây không có chu trình Euler. Các đồ thị này có đỉnh bậc lẻ không?
Giải:
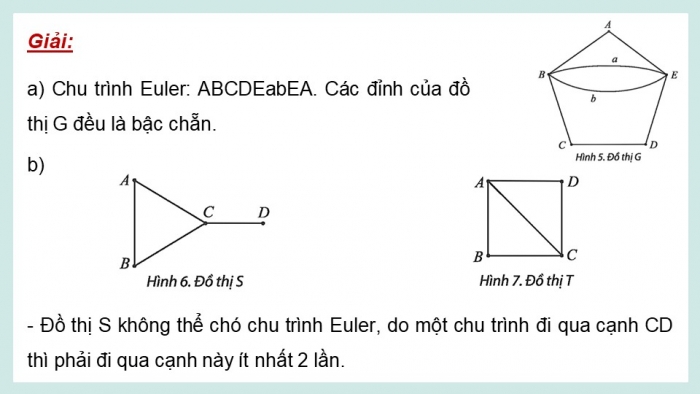
a) Chu trình Euler: ABCDEabEA. Các đỉnh của đồ thị G đều là bậc chẵn.
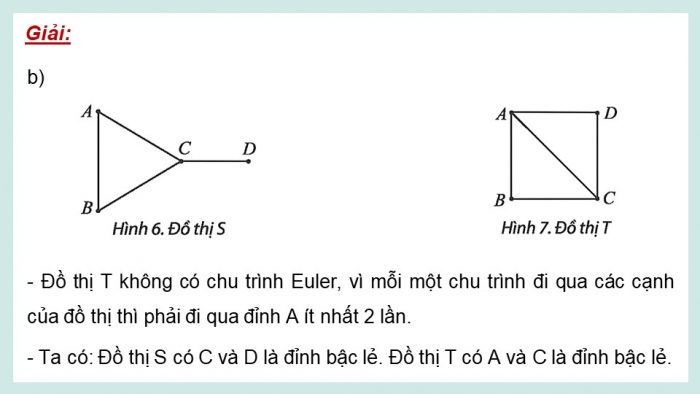
b)
- Đồ thị S không thể chó chu trình Euler, do một chu trình đi qua cạnh CD thì phải đi qua cạnh này ít nhất 2 lần.
- Đồ thị T không có chu trình Euler, vì mỗi một chu trình đi qua các cạnh của đồ thị thì phải đi qua đỉnh A ít nhất 2 lần.
- Ta có: Đồ thị S có C và D là đỉnh bậc lẻ. Đồ thị T có A và C là đỉnh bậc lẻ.
ĐỊNH LÍ 1
Đồ thị liên thông G có chu trình Euler khi và chỉ khi mọi đỉnh của nó đều có bậc chẵn.
Ví dụ 3:Mỗi đồ thị sau đây có chu trình Euler không? Nếu có, hãy chỉ ra một chu trình như vậy.
Giải:
a) Đồ thị G không có chu trình Euler, vì có đỉnh B bậc 3 là bậc lẻ.
b) Ta thấy tất cả các đình của đồ thị H đều có bậc chẵn nên H có chu trình Euler, chẳng hạn, AEBCDFCABDA.
HĐKP3
Hãy chỉ ra một đường đi Euler trên mỗi đồ thị sau. Mỗi đồ thị có bao nhiêu đỉnh bậc lẻ?
Giải:
- Đường đi Euler của đồ thị G: ACBDab
- Đường đi Euler của đồ thị H: EABFEDCF
- Mỗi đồ thị có 2 đỉnh bậc lẻ (bậc 3).
Định lí 2
Đồ thị liên thông G có đường đi Euler nhưng không có chu trình Euler nếu và chỉ nếu nó có đúng hai đỉnh bậc lẻ.
Khi đó, đường đi Euler đi từ đỉnh bậc lẻ này đến đỉnh bậc lẻ kia.
Ví dụ 4:Mỗi đồ thị trong Hình 10 có đường đi Euler không? Nếu có, hãy chỉ ra một đường đi như vậy.
Giải:
a) Đồ thị G không có đường đi Euler, có đến 4 đỉnh bậc lẻ là A, B, C, D.
b) Đồ thị H có đúng hai đỉnh bậc lẻ là B và C nên nó có đường đi Euler. Chẳng hạn, đường đi BAEabEDCBFC là một đường đi Euler trên H.
Ví dụ 5:Có năm vùng đất A, B, C, D và E được nối với nhau bởi những cây cầu như Hình 11. Có hay không một cách đi qua tất cả các cây cầu, mỗi cây cầu chỉ qua một lần và quay trở lại nơi xuất phát ban đầu? Nếu có, hãy chỉ ra một cách đi như vậy.
Giải:
Biểu thị mỗi vùng đất bằng một đỉnh, mỗi cây cầu bằng một cạnh nối hai đỉnh, ta được đồ thị như Hình 12.
Ta thấy các đỉnh của đồ thị đều có bậc chẵn.
Do đó, đồ thị có chu trình Euler.
Nói cách khác, có cách đi qua tất cả các cây cầu, mỗi cây cầu chỉ đi qua một lần và quay trở lại nơi xuất phát ban đầu.
Chẳng hạn, bắt đầu từ D, ta có thể đi theo chu trình Euler: DAabACBED.
THỰC HÀNH 1
Mỗi đồ thị sau đây có chu trình Euler không? Nếu có, hãy chỉ ra một chu trình như vậy.
Giải:
- Đồ thị G có chu trình Euler vì tất cả các đỉnh đều có bậc chẵn (bằng 4).
Một chu trình Euler của đồ thị G là: ADBECABCDEA
- Đồ thị H không có chu trình Euler, vì đỉnh B và đỉnh C có bậc lẻ (bằng 3).
THỰC HÀNH 2
Đồ thị sau có đường đi Euler không? Nếu có, hãy chỉ ra một đường đi như vậy.
Giải:
Đồ thị H có đường đi Euler, vì có đúng hai đỉnh bậc lẻ là E và F.
Chẳng hạn, có đường đi Euler: EBabBCcdCFDAEF.
--------------- Còn tiếp ---------------
Trên chỉ là 1 phần của giáo án. Giáo án khi tải về có đầy đủ nội dung của bài. Đủ nội dung của học kì I + học kì II
Hệ thống có đủ tài liệu:
- Giáo án điện tử chuyên đề Toán 11 chân trời sáng tạo (350k)
- Giáo án toán 11 chân trời sáng tạo (300k)
- Giáo án chuyên đề toán 11 chân trời sáng tạo (300k)
- Giáo án powerpoint toán 11 chân trời sáng tạo (350k)
- Giáo án dạy thêm toán 11 chân trời sáng tạo (300k)
- Câu hỏi và bài tập trắc nghiệm toán 11 chân trời sáng tạo (150k)
- Đề thi toán 11 chân trời sáng tạo (150k)
- File bài tập toán 11 chân trời sáng tạo (150k)
- File word đáp án toán 11 chân trời sáng tạo (100k)
- Bài tập file word toán 11 chân trời sáng tạo (150k)
- Kiến thức trọng tâm Toán 11 chân trời sáng tạo (150k)
- Đề kiểm tra 15 phút Toán 11 chân trời sáng tạo (100k)
- Giáo án powerpoint chuyên đề toán 11 chân trời sáng tạo (350k)
- Phiếu học tập theo bài Toán 11 chân trời sáng tạo cả năm (150k)
- Trắc nghiệm đúng sai Toán 11 chân trời sáng tạo cả năm (150k)
- Trắc nghiệm dạng câu trả lời ngắn Toán 11 chân trời sáng tạo cả năm (150k)
=> Có thể chọn nâng cấp VIP với phí là 1050k để tải tất cả tài liệu ở trên
- Chỉ gửi 500k. Tải về dùng thực tế, 1 ngày sau mới gửi số còn lại.
Cách tải hoặc nâng cấp:
- Bước 1: Chuyển phí vào STK: 1214136868686 - cty Fidutech - MB
- Bước 2: Nhắn tin tới Zalo Fidutech - nhấn vào đây để thông báo và nhận tài liệu
Xem toàn bộ: Giáo án điện tử chuyên đề Toán 11 chân trời sáng tạo
ĐẦY ĐỦ GIÁO ÁN CÁC BỘ SÁCH KHÁC
GIÁO ÁN WORD LỚP 11 CHÂN TRỜI SÁNG TẠO
GIÁO ÁN POWERPOINT LỚP 11 CHÂN TRỜI SÁNG TẠO
GIÁO ÁN CHUYÊN ĐỀ 11 CHÂN TRỜI SÁNG TẠO
GIÁO ÁN DẠY THÊM 11 CHÂN TRỜI SÁNG TẠO
CÁCH ĐẶT MUA:
Liên hệ Zalo: Fidutech - nhấn vào đây