Đề thi toán 12 kết nối tri thức có ma trận
Ma trận đề thi, đề kiểm tra Toán 12 kết nối tri thức. Cấu trúc của đề thi gồm: Đề thi (trắc nghiệm, trắc nghiệm Đ/S, trắc nghiệm trả lời ngắn), hướng dẫn chấm điểm, bảng năng lực và cấp độ tư duy, bảng đặc tả kĩ thuật. Bộ tài liệu có nhiều đề thi giữa kì 1, cuối kì 1, giữa kì 2, cuối kì 2. Tài liệu là bản word, có thể tải về và điều chỉnh những chỗ cần thiết. Thầy cô kéo xuống xem chi tiết
Click vào ảnh dưới đây để xem giáo án rõ







Một số tài liệu quan tâm khác
Phần trình bày nội dung giáo án
SỞ GD & ĐT ………………. | Chữ kí GT1: ........................... |
TRƯỜNG THPT………………. | Chữ kí GT2: ........................... |
ĐỀ KIỂM TRA GIỮA HỌC KÌ I
TOÁN 12 – KẾT NỐI TRI THỨC
NĂM HỌC: 2024 - 2025
Thời gian làm bài: 90 phút (Không kể thời gian phát đề)
Họ và tên: …………………………………… Lớp: ……………….. Số báo danh: …………………………….……Phòng KT:………….. | Mã phách |
![]()
Điểm bằng số
| Điểm bằng chữ | Chữ ký của GK1 | Chữ ký của GK2 | Mã phách |
PHẦN I. Câu trắc nghiệm nhiều phương án lực chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chọn một phương án.
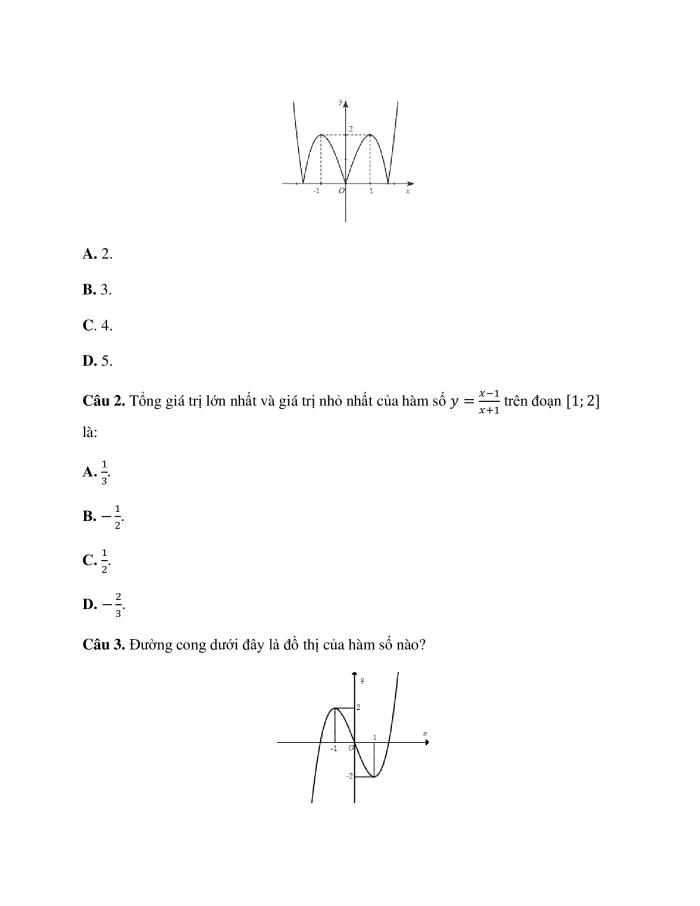
Câu 1. Cho hàm số ![]() liên tục trên
liên tục trên ![]() và có đồ thị như hình vẽ. Hỏi hàm số có bao nhiêu điểm cực trị?
và có đồ thị như hình vẽ. Hỏi hàm số có bao nhiêu điểm cực trị?
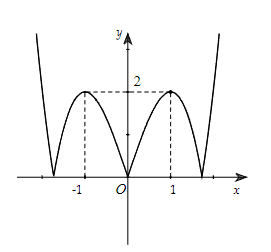
A. 2.
B. 3.
C. 4.
D. 5.
Câu 2. Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số ![]() trên đoạn
trên đoạn ![]() là:
là:
A. ![]()
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Câu 3. Đường cong dưới đây là đồ thị của hàm số nào?
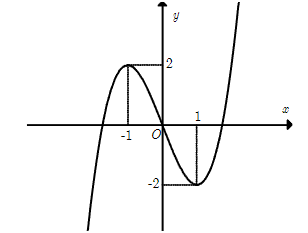
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Câu 4. Cho hàm số ![]() có bảng biến thiên như sau:
có bảng biến thiên như sau:

Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A. ![]()
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Câu 5. Đường tiệm cận ngang của đồ thị hàm số ![]() có phương trình là:
có phương trình là:
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Câu 6. Hàm số ![]() nghịch biến trên khoảng:
nghịch biến trên khoảng:
A. ![]() .
.
B. ![]()
C. ![]() .
.
D. ![]() .
.
Câu 7. Cho hàm số ![]() có đồ thị là đường cong
có đồ thị là đường cong ![]() và các giới hạn
và các giới hạn ![]() ;
; ![]() ;
;![]() . Hỏi mệnh đề nào sau đây đúng?
. Hỏi mệnh đề nào sau đây đúng?
A. Đường thẳng ![]() là tiệm cận đứng của
là tiệm cận đứng của ![]() .
.
B. Đường thẳng ![]() là tiệm cận ngang của
là tiệm cận ngang của ![]() .
.
C. Đường thẳng ![]() là tiệm cận ngang của
là tiệm cận ngang của ![]() .
.
D. Đường thẳng ![]() là tiệm cận đứng của
là tiệm cận đứng của ![]() .
.
Câu 8. Cho hàm số ![]() liên tục trên
liên tục trên ![]() và có bảng biến thiên như sau:
và có bảng biến thiên như sau:

Tìm giá trị lớn nhất của hàm số ![]() trên đoạn
trên đoạn ![]() .
.
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Câu 9. Cho hình chóp ![]() , với
, với ![]() là giao điểm của
là giao điểm của ![]() và
và ![]() . Mệnh đề nào sau đây là đúng?
. Mệnh đề nào sau đây là đúng?
A. Nếu ![]() là hình bình hành thì
là hình bình hành thì ![]() .
.
B. Nếu ![]() thì
thì ![]() là hình bình hành.
là hình bình hành.
C. Nếu ![]() là hình bình hành thì
là hình bình hành thì ![]() .
.
D. Nếu ![]() thì
thì ![]() là hình bình hành.
là hình bình hành.
Câu 10. Cho hàm số ![]() có đồ thị
có đồ thị ![]() . Phương trình tiếp tuyến với đồ thị
. Phương trình tiếp tuyến với đồ thị ![]() tại giao điểm của
tại giao điểm của ![]() với trục tung là:
với trục tung là:
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Câu 11. Cho tứ diện ![]() có trọng tâm
có trọng tâm ![]() . Mệnh đề nào sau đây là sai?
. Mệnh đề nào sau đây là sai?
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Câu 12. Cho ![]() có đồ thị
có đồ thị ![]() với
với ![]() là tham số. Các đồ thị
là tham số. Các đồ thị ![]() luôn đi qua hai điểm cố định có tọa độ là:
luôn đi qua hai điểm cố định có tọa độ là:
A. ![]() và
và ![]() .
.
B. ![]() và
và ![]() .
.
C. ![]() và
và ![]() .
.
D. ![]() và
và ![]() .
.
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1. Cho hàm số ![]() liên tục trên
liên tục trên ![]() và có bảng biến thiên:
và có bảng biến thiên:

a) Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng ![]() .
.
b) Hàm số đã cho có cực tiểu bằng ![]() và
và ![]() .
.
c) Hàm số đồng biến trên khoảng ![]() ).
).
d) Đường thẳng ![]() cắt đồ thị hàm số tại 2 điểm.
cắt đồ thị hàm số tại 2 điểm.
Câu 2. Cho hàm số ![]() .
.
a) Hàm số đã cho đồng biến trên khoảng ![]() và
và ![]() .
.
b) Hàm số đã cho có 2 cực trị.
c) Đồ thị hàm số nhận điểm ![]() là tâm đối xứng.
là tâm đối xứng.
d) Có 5 điểm thuộc đồ thị hàm số có tọa độ nguyên.
Câu 3. Cho hình lập phương ![]() . Gọi
. Gọi ![]() là tâm của hình lập phương. Khi đó:
là tâm của hình lập phương. Khi đó:
a) ![]() .
.
b) ![]() ).
).
c) Góc giữa hai vectơ ![]() và
và ![]() bằng
bằng ![]() .
.
d) ![]() .
.
Câu 4. Cho hình chóp ![]() có đáy
có đáy ![]() là hình bình hành tâm
là hình bình hành tâm ![]() . Khi đó:
. Khi đó:
a) ![]() .
.
b) ![]()
c) Nếu G là điểm thỏa mãn ![]() thì
thì ![]() thẳng hàng.
thẳng hàng.
d) ![]() .
.
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1. Tìm tất cả các giá trị của tham số ![]() để hàm số
để hàm số ![]() đạt cực tiểu tại
đạt cực tiểu tại ![]() .
.
Câu 2. Một người bán gạo muốn đóng một thùng tôn có hình dạng là hình hộp chữ nhật để đựng gạo với thể tích bằng ![]() . Trên thị trường, giá tôn làm đáy thùng là 100 000 đồng/
. Trên thị trường, giá tôn làm đáy thùng là 100 000 đồng/![]() và giá tôn làm thành xung quanh thùng là 50 000 đồng/
và giá tôn làm thành xung quanh thùng là 50 000 đồng/![]() . Hỏi, người bán gạo cần đóng thùng đựng gạo với cạnh đáy bằng bao nhiêu để chi phí mua nguyên liệu là nhỏ nhất? Biết đáy thùng là hình vuông và không có nắp.
. Hỏi, người bán gạo cần đóng thùng đựng gạo với cạnh đáy bằng bao nhiêu để chi phí mua nguyên liệu là nhỏ nhất? Biết đáy thùng là hình vuông và không có nắp.
Câu 3. Đồ thị của hàm số ![]() có hai điểm cực trị
có hai điểm cực trị ![]() và
và ![]() . Tính diện tích
. Tính diện tích ![]() của tam giác
của tam giác ![]() với
với ![]() là gốc tọa độ.
là gốc tọa độ.
Câu 4. Cho hình chóp ![]() có đáy là hình vuông cạnh
có đáy là hình vuông cạnh ![]() , cạnh bên
, cạnh bên ![]() vuông góc với đáy,
vuông góc với đáy, ![]() . Gọi
. Gọi ![]() là trung điểm của
là trung điểm của ![]() Tính góc giữa hai vectơ
Tính góc giữa hai vectơ ![]() và
và ![]() .
.
Câu 5. Cho hàm số ![]() có bảng biến thiên như hình dưới đây. Tìm giá trị lớn nhất của hàm số
có bảng biến thiên như hình dưới đây. Tìm giá trị lớn nhất của hàm số ![]() trên đoạn
trên đoạn ![]() .
.

Câu 6. Gọi ![]() lần lượt là trung điểm của các cạnh
lần lượt là trung điểm của các cạnh ![]() và
và ![]() của tứ diện
của tứ diện ![]() . Gọi
. Gọi ![]() là trung điểm của đoạn
là trung điểm của đoạn ![]() và
và ![]() là một điểm bất kỳ trong không gian. Tìm giá trị thực của
là một điểm bất kỳ trong không gian. Tìm giá trị thực của ![]() thỏa mãn đẳng thức vectơ
thỏa mãn đẳng thức vectơ ![]() .
.
TRƯỜNG THPT ........
HƯỚNG DẪN CHẤM KIỂM TRA GIỮA HỌC KÌ 1 (2024 – 2025)
MÔN: TOÁN 12 – KẾT NỐI TRI THỨC
PHẦN I
(Mỗi câu trả lời đúng thí sinh được 0,25 điểm)
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
D | A | B | A | C | C | B | C | D | D | A | D |
PHẦN II
Điểm tối đa của 01 câu hỏi là 1 điểm.
- Thí sinh chỉ lựa chọn chính xác 01 ý trong 1 câu hỏi được 0,1 điểm.
- Thí sinh chỉ lựa chọn chính xác 02 ý trong 1 câu hỏi được 0,25 điểm.
- Thí sinh chỉ lựa chọn chính xác 03 ý trong 1 câu hỏi được 0,5 điểm.
- Thí sinh lực chọn chính xác cả 04 ý trong 1 câu hỏi được 1 điểm.
Câu | Câu 1 | Câu 2 | Câu 3 | Câu 4 |
a) | S | Đ | Đ | S |
b) | Đ | S | Đ | Đ |
c) | S | Đ | S | Đ |
d) | Đ | S | S | S |
PHẦN III
(Mỗi câu trả lời đúng thí sinh được 0,5 điểm)
Câu | 1 | 2 | 3 | 4 | 5 | 6 |
Trả lời |
| 2m | 5 | 120 | 12 |
|
TRƯỜNG THPT .........
BẢNG NĂNG LỰC VÀ CẤP ĐỘ TƯ DUY
MÔN: TOÁN 12 – KẾT NỐI TRI THỨC
Năng lực | Cấp độ tư duy | |||||
Chương I. Ứng dụng đạo hàm để khảo sát hàm số | Chương II. Vectơ và hệ tọa độ trong không gian | |||||
Nhận biết | Thông hiểu | Vận dụng | Nhận biết | Thông hiểu | Vận dụng | |
Tư duy và lập luận Toán học | 6 | 3 | 0 | 3 | 2 | 1 |
Giải quyết vẫn đề Toán học | 4 | 5 | 2 | 2 | 3 | 1 |
Mô hình hóa Toán học | 0 | 0 | 2 | 0 | 0 | 0 |
Tổng | 10 | 8 | 4 | 5 | 5 | 2 |
TRƯỜNG THPT .........
BẢN ĐẶC TẢ KĨ THUẬT ĐỀ KIỂM TRA GIỮA HỌC KÌ 1 (2024 – 2025)
MÔN: TOÁN 12 – CÁNH DIỀU
Nội dung | Cấp độ | Năng lực | Số ý/câu | Câu hỏi | ||||||
Tư duy và lập luận toán học | Giải quyết vấn đề | Mô hình hóa | TN nhiều đáp án (số ý) | TN đúng sai (số ý) | TN ngắn (số câu) | TN nhiều đáp án (số ý) | TN đúng sai (số ý) | TN ngắn (số câu) | ||
Chương I. Ứng dụng đạo hàm để khảo sát hàm số |
|
|
| 10 | 8 | 4 | ||||
Bài 1. Tính đơn điệu và cực trị của hàm số | Nhận biết | Nhận biết được tính đơn điệu, điểm cực trị, giá trị cực trị của hàm số thông qua bảng biến thiên hoặc thông qua hình ảnh của đồ thị |
| . | 2 | 2 |
| C1; C4 | C1b; C1c |
|
Thông hiểu | Xét tính đồng biến, nghịch biến của một hàm số trên một khoảng dựa vào dấu của đạo hàm cấp một của nó. | Thể hiện được tính đồng biến, nghịch biến của hàm số trong bảng biến thiên |
| 1 | 2 |
| C6 | C2a; C2b |
| |
Vận dụng |
|
| Vận dụng đạo hàm và tính đơn điệu của hàm số để giải quyết một số bài toán thực tiễn. |
|
| 1 |
|
| C1 | |
Bài 2. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số | Nhận biết | Nhận biết được giá trị lớn nhất, giá trị nhỏ nhất của hàm số dựa vào đồ thị và bảng biến thiên. |
|
| 1 | 1 |
| C8 | C1a |
|
Thông hiểu |
| Xác định được giá trị lớn nhất, giá trị nhỏ nhất của hàm số bằng đạo hàm trong những trường hợp đơn giản. |
| 1 |
|
| C2 |
|
| |
Vận dụng |
|
| Ứng dụng giải các bài toán thực tiễn. |
| 2 |
|
|
| C2; C5 | |
Bài 3. Đường tiệm cận của đồ thị hàm số | Nhận biết | Nhận biết được định nghĩa về đường tiệm cận đứng, tiệm cận ngang và tiệm cận xiên của đồ thị hàm số. |
|
| 2 |
|
| C5; C7 |
|
|
Thông hiểu | Xác định được các đường tiệm cận của đồ thị hàm số. |
|
|
|
|
|
|
|
| |
Vận dụng |
| Tìm các điều kiện để hàm số có tiệm cận. |
|
|
|
|
|
|
| |
Bài 4. Khảo sát và vẽ đồ thị của một số hàm số cơ bản | Nhận biết |
| Đọc đồ thị. |
| 1 | 1 |
| C3 | C1d |
|
Thông hiểu | Khảo sát và vẽ được đồ thị của các hàm số bậc ba và phân thức. |
|
| 2 | 2 |
| C10; C12 | C2c; C2d |
| |
Vận dụng |
|
| Vận dụng đạo hàm và khảo sát hàm số để giải quyết một số vấn đề liên quan đến thực tiễn. |
|
| 1 |
|
| C3 | |
Chương II. Vectơ và hệ tọa độ trong không gian |
|
|
| 2 | 8 | 2 | ||||
Bài 1. Vectơ và các phép toán trong không gian | Nhận biết | Nhận biết được định nghĩa vectơ và các phép toán vectơ trong không gian. |
|
| 1 | 4 |
| C9 | C3a; C3b; C4a; C4d |
|
Thông hiểu | Áp dụng quy tắc ba điểm, quy tắc hình bình hành, quy tắc hình hộp để biểu diễn các vectơ. -Tính được góc và tích vô hướng của hai vec tơ
| Chứng minh các đẳng thức vectơ. |
| 1 | 4 |
| C11 | C3c; C3d; C4b; C4c |
| |
Vận dụng | Tìm điều kiện để vectơ đồng phẳng. |
| Ứng dụng vectơ vào các bài toán thực tế và liên hệ giữa các môn học khác. |
|
| 2 |
|
| C4; C6 | |

Đủ kho tài liệu môn học
=> Tài liệu sẽ được gửi ngay và luôn
Cách tải:
- Bước 1: Chuyển phí vào STK: 1214136868686 - cty Fidutech - MB
- Bước 2: Nhắn tin tới Zalo Fidutech - nhấn vào đây để thông báo và nhận tài liệu
=> Giáo án toán 12 kết nối tri thức
Từ khóa: đề thi giữa kì 1 toán 12 kết nối tri thức, đề thi cuối kì 1 toán 12 kết nối tri thức, đề thi toán 12 sách kết nối tri thức, đề thi toán 12 sách kết nối tri thức mớiTài liệu giảng dạy môn Toán THPT
