Giáo án và PPT Toán 10 kết nối Bài 10: Vectơ trong mặt phẳng toạ độ

CHƯƠNG IV: VECTƠ

BÀI 10. VECTƠ TRONG MẶT PHẲNG TỌA ĐỘ

HOẠT ĐỘNG KHỞI ĐỘNG

GV yêu cầu HS thảo luận và trả lời:

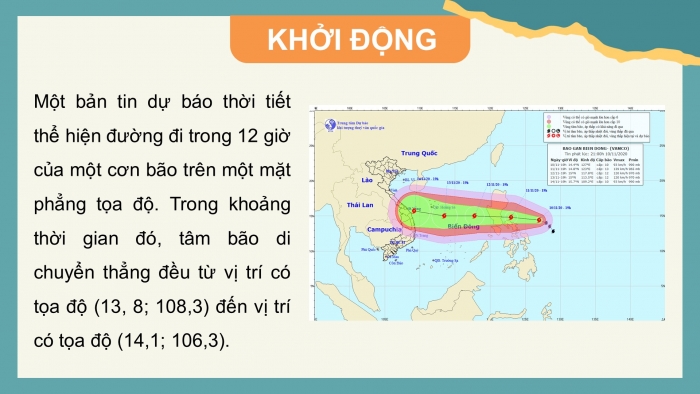
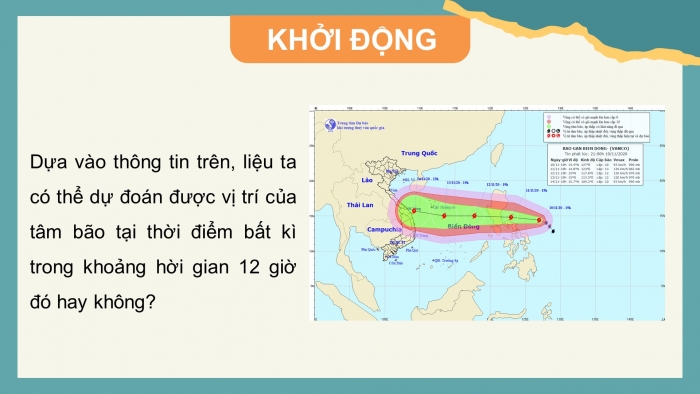
Một bản tin dự báo thời tiết thể hiện đường đi trong 12 giờ của một cơn bão trên một mặt phẳng tọa độ. Trong khoảng thời gian đó, tâm bāo di chuyển thẳng đều từ vị trí có tọa độ (13,8; 108,3) đến vị trí có toạ độ (14,1;106,3). Dựa vào thông tin trên, liệu ta có thể dự đoán được vị trí của tâm bão tại thời điểm bất kì trong khoảng thời gian 12 giờ đó hay không?

HOẠT ĐỘNG HÌNH THÀNH KIẾN THỨC

HOẠT ĐỘNG 1. TỌA ĐỘ CỦA VECTƠ

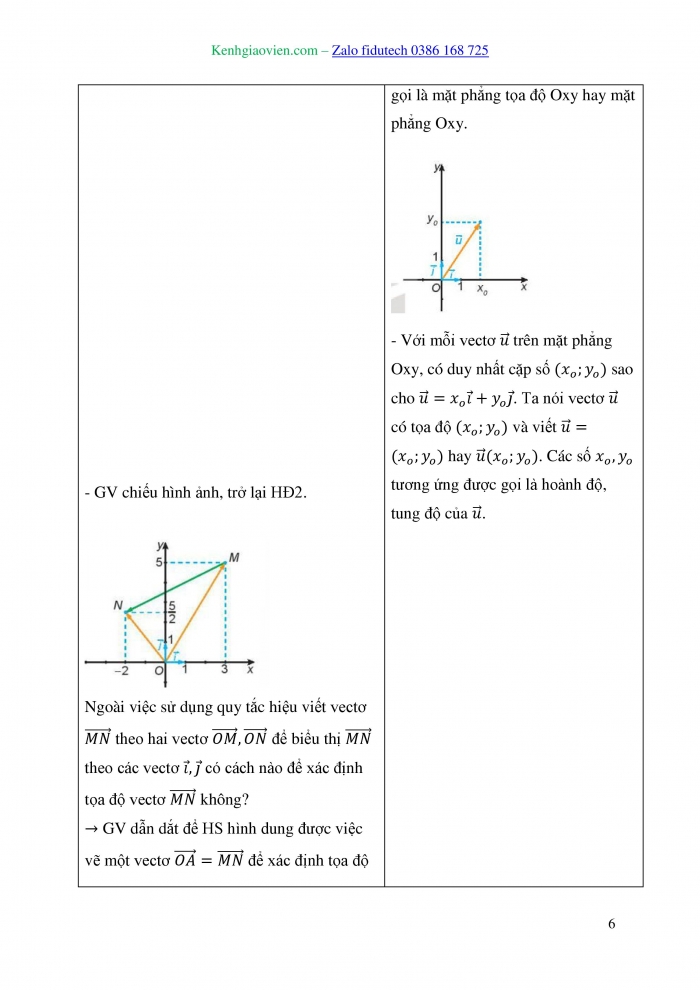
GV đặt câu hỏi hướng dẫn học sinh tìm hiểu: Trên trục số Ox, gọi A là điểm biểu diễn số 1 và đặt −−→OA=→iOA→=i→ (H.4.32a). Gọi M là điểm biểu diễn số 4, N là điểm biểu diễn số −32−32. Hãy biểu thị mỗi vectơ −−→OM,−−→ONOM→,ON→ theo vectơ →ii→.

Sản phẩm dự kiến:

Do A biểu diễn số 1, M biểu diễn số 4, nên hai vectơ và có cùng phương, cùng hướng và .

Suy ra .

Cũng vậy, do A biểu diễn số 1, N biểu diễn số nên hai vectơ và có cùng phương, ngược hướng và .

Suy ra .

- Trục tọa độ (còn gọi là trục, hay trục số) là một đường thẳng mà trên đó đã xác định một điểm O và một vectơ có độ dài bằng 1. 

Điểm O gọi là gốc tọa độ, vectơ gọi là vectơ đơn vị của trục. Điểm M trên trục biểu diễn số x_o nếu .

HOẠT ĐỘNG 2. BIỂU THỨC TỌA ĐỘ CỦA CÁC PHÉP TOÁN VECTƠ 

GV đưa ra câu hỏi: Trong mặt phẳng tọa độ Oxy, cho 

→u=(2;−3),→v=(4;1),→a=(8;−12)u→=(2;−3),v→=(4;1),a→=(8;−12)

a) Hãy biểu thị mỗi vectơ →u,→v,→au→,v→,a→ theo các vectơ →i,→ji→,j→

b) Tìm tọa độ của các vectơ →u+→v,4.→uu→+v→,4.u→

c) Tìm mối liên hệ giữa hai vectơ →u,→a

Sản phẩm dự kiến:

HĐ3:

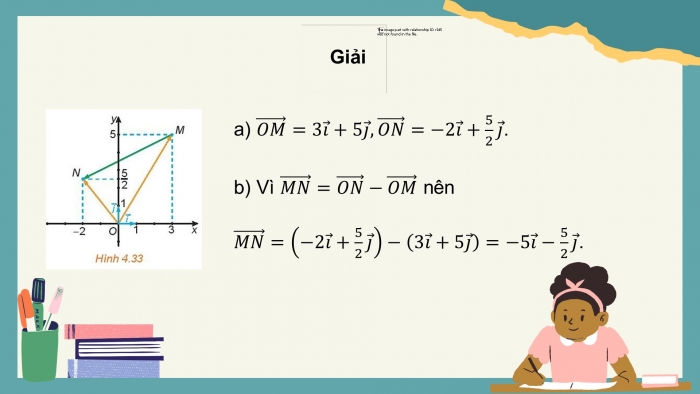
a) .

b) Vì

nên .

Vì nên .

Suy ra .

c) Vì và 

nên .

HOẠT ĐỘNG LUYỆN TẬP

Từ nội dung bài học,GV yêu cầu HS hoàn thành các bài tập trắc nghiệm sau:

Câu 1: Trong mặt phẳng tọa độ Oxy, cho các điểm M(1;3), N(4;2). Nhận xét nào sau đây đúng nhất về tam giác OMN.

A. Tam giác OMN là tam giác đều;

B. Tam giác OMN vuông cân tại M;

C. Tam giác OMN vuông cân tại N;

D. Tam giác OMN vuông cân tại O.

Câu 2: Trong mặt phẳng tọa độ Oxy, cho hai điểm A(2;1), B(3;3). Tìm điểm M(x;y) để OABM là một hình bình hành.

A. M(1; 2);

B. M(-1; 2);

C.M(1; -2);

D. M(-1; -2)

Câu 3:  Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có G là trọng tâm. Cho tọa độ các điểm A(1;3), B(2;4), G(-3;2). Tọa độ điểm C là:

A. C(0; 3);

B. C(-6; -5);

C. C(-12; -1);

D. C(0; 9).

Câu 4: Trong các vectơ sau đây, có bao nhiêu cặp vectơ cùng phương?

x→(−1;3);y→(2;−13);z→(−25;15);w→(4;−2)

A. Có 1 cặp;

B. Có 3 cặp;

C. Có 4 cặp;

D. Có 0 cặp.

Câu 5: Trong mặt phẳng tọa độ Oxy, cho u→=−5i→+6j→. Khi đó tọa độ của vectơ u→ là:

A. u→(5; 6);

B. u→-5; -6);

C. u→(6; -5);

D. u→(-5; 6).

Sản phẩm dự kiến:

HOẠT ĐỘNG VẬN DỤNG

Vận dụng kiến thức, GV yêu cầu HS hoàn thành bài tập sau:

Câu 1:  Trong mặt phẳng tọa độ Oxy, cho các điểm M(1; 3), N(4; 2)

a) Tính độ dài các đoạn thẳng OM, ON, MN.

b) Chứng minh rằng tam giác OMN vuông cân.

Câu 2: Trong mặt phẳng tọa độ Oxy, cho hai điểm A(2; 1), B(3; 3).

a) Các điểm O, A, B có thẳng hàng hay không?

b) Tìm điểm M(x; y) để OABM là một hình hành.