Trắc nghiệm câu trả lời ngắn Toán 11 cánh diều Bài 4: Hai mặt phẳng song song

BÀI 4. HAI MẶT PHẲNG SONG SONG

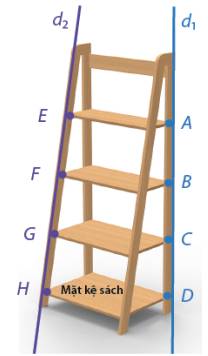
Câu 1: Hình ảnh dưới đây là kệ sách gỗ có 4 mặt kệ với thanh gỗ đứng và thanh gỗ xiên. Giá đỡ các mặt kệ xuất hiện ở các vị trí và . Biết và cách đều nhau và các mặt kệ song song với mặt đất. Tính độ dài đoạn .

• 105

Câu 2: Cho hình chóp có đáy là tam giác thỏa mãn Mặt phẳng song song với cắt đoạn tại sao cho Giao tuyến của mặt phẳng và các mặt (SAB), (SBC), (SAC) tạo thành một tam giác có diện tích là là phân số tối giản. Tính giá trị của

• 7

Câu 3:Cho hình chóp có đáy là hình thang cân với cạnh bên hai đáy Mặt phẳng song song với và cắt cạnh tại sao cho Giao tuyến của mặt phẳng và các mặt (SAB), (SBC), (SCD), (SAD) tạo thành một tứ giác có diện tích là là phân số tối giản. Tính .

• -4

Câu 4: Cho hình chóp có đáy là hình thang, và . Gọi là giao điểm của và . Lấy thuộc cạnh , thuộc cạnh sao cho .

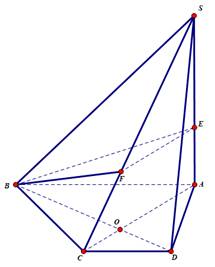
Gọi là mặt phẳng qua và song song với mặt phẳng . Gọi là giao điểm của với . Tính tỉ số , biết và . Tính giá trị biểu thức .

• 9

Câu 5: Người ta muốn thiết kế trại chào mừng ngày 26/03 có dạng như hình dưới.

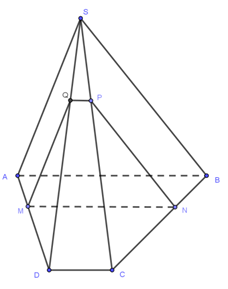
Hình chóp có đáy là hình thang , cạnh , . Tam giác cân tại . Mặt phẳng song song với cắt các cạnh theo thứ tự tại . Đặt . Biết tứ giác thì , Tính

• 3

BÀI TẬP THAM KHẢO THÊM

Câu 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O, gọi M, N lần lượt là trung điểm của SA, SD. Chứng minh rằng (OMN) // (SBC)

Trả lời: (OMN) // (SBC)

Câu 2:  Cho hình chóp S.ABCD có đáy là một hình bình hành. Gọi A′, B′, C′, D′ lần lượt là trung điểm của các cạnh SA, SB, SC, SD. Chứng minh rằng (A′B′C′D′) // (ABCD)

Trả lời: (A′B′C′D′) // (ABCD)

Câu 3:  Cho hình chóp S.ABCD với đáy ABCD là hình thang mà AD//BC và AD = 2BC. Gọi M, N lần lượt là trung điểm của SA và AD. Chứng minh: (BMN) // (SCD)

Trả lời: (BMN) // (SCD)

Câu 4: Cho hai hình bình hành ABCD và ABEF có chung cạnh AB và không đồng phẳng. Gọi I, J, K lần lượt là trung điểm AB, CD, EF. Chứng minh: (DIK) // (JBE)

Trả lời: (DIK) // (JBE)

Câu 5: Cho hình lăng trụ ABC.A′B′C′. Gọi I, J, K lần lượt là trọng tâm các tam giác ABC, ACC′, A′B′C′. Chứng minh rằng: (IJK) // (BCC′B′) và (A′JK) // (AIB′)

Trả lời: (IJK) // (BCC′B′) và (A′JK) // (AIB′)

Câu 6:  Cho hai hình vuông ABCD và ABEF ở trong hai mặt phẳng phân biệt. Trên các đường chéo AC và BF lần lượt lấy các điểm M, N sao cho AM = BN. Các đường thẳng song song với AB vẽ từ M, N lần lượt cắt AD và AF tại M′ và N′. Chứng minh rằng (CDF) // (MM′N′)

Trả lời: ………………………………………

Câu 7:  Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi G₁,G₂,G₃ ​ lần lượt là trọng tâm các tam giác SAB, ABC, SBD. Gọi M là một điểm thuộc đường thẳng G₂G₃ ​. Chứng minh G₁M // (SBC)

Trả lời: ………………………………………

Câu 8:  Cho lăng trụ tam giác ABC.A’B’C’. Gọi M, N lần lượt là trung điểm của BB’, CC’. Đường thẳng qua đi qua trọng tâm I của tam giác ABC cắt A’B và MN lần lượt tại P,Q. Khi đó tỷ số IP/IQ bằng bao nhiêu ?

Trả lời: ………………………………………

Câu 9:  Cho tứ diện đều S.ABC. Gọi I là trung điểm của AB, M là một điểm di động trên đoạn AI. Gọi (P) là mặt phẳng qua M và song song với (SIC). Thiết diện tạo bởi (P) và tứ diện S.ABC là?

Trả lời: ………………………………………

Câu 10: Cho tứ diện ABCD có AB = 6, CD = 8. Cắt tứ diện bởi một mặt phẳng song song với AB, CD để thiết diện thu được là một hình thoi. Cạnh của hình thoi đó bằng bao nhiêu ?

Trả lời: ………………………………………

Câu 11:  Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Gọi M là trung điểm của AB, N là tâm hình vuông AA’D’D. Tính diện tích thiết diện của hình lập phương ABCD.A’B’C’D’ tạo bởi mặt phẳng (CMN).

Trả lời: ………………………………………

Câu 12:  Cho hình chóp S.ABCD có đáy là hình bình hành ABCD tâm O. AB = 8, SA = SB = 6. (P) là mặt phẳng qua O và song song với (SAB). Tính diện tích thiết diện của hình chóp với (P) 

Trả lời: ………………………………………

Câu 13: Cho hình chóp S.ABCD có đáy là hình thang ABCD, AB//CD, AB = 2CD. M là điểm thuộc cạnh AD, (α) là mặt phẳng qua M và song song với mặt phẳng (SAB). Biết diện tích thiết diện của hình chóp cắt bởi mặt phẳng (α) bằng 2/3 diện tích tam giác SAB. Tính tỉ số x =

Trả lời: ………………………………………

Câu 14: Cho tứ diện ABCD có tất cả các cạnh đều bằng a, điểm G là trọng tâm của tam giác BCD. Gọi (P) là mặt phẳng đi qua G và song song với mặt phẳng (ABC). Tính diện tích S của thiết diện tạo bởi mặt phẳng (P) và tứ diện ABCD

Trả lời: ………………………………………

Câu 15: Cho hình chóp S.ABCD đáy là hình thang, đáy lớn BC = 2a, AD = a, AB = b. Mặt bên (SAD) là tam giác đều. Mặt phẳng (a) qua điểm M trên cạnh AB và song song với các cạnh SA và BC. Mặt phẳng (a) cắt CD, SC, SB lần lượt tại N, P, Q. Đặt x = AM (0 < x < b). Tính giá trị lớn nhất của diện tích thiết diện tạo bởi (a) và hình chóp S.ABCD

Trả lời: ………………………………………

Câu 16:  Cho hình hộp ABCD.A’B’C’D’. Trên cạnh AB lấy điểm M khác A và B . Gọi (P) là mặt phẳng đi qua M và song song với mặt phẳng ( ACD¢). Đặt = k, 0 < k < 1. Tìm k để thiết diện của hình hộp và mặt phẳng (P) có diện tích lớn nhất.

Trả lời: ………………………………………

Câu 17:  Cho hình bình hành ABCD. Gọi Bx, Cy, Dz là các đường thẳng song song với nhau lần lượt đi qua B, C, D và nằm về một phía của mặt phẳng (ABCD) , đồng thời không nằm trong mặt phẳng (ABCD) . Một mặt phẳng đi qua A cắt Bx, Cy, Dz lần lượt tại B’, C’, D’ với BB’ = 2; DD’ = 4. Khi đó độ dài CC¢ bằng bao nhiêu? 

Trả lời: ………………………………………

Câu 18:  Cho hình tứ diện ABCD. Gọi I, J, K lần lượt là trọng tâm của các tam giác ABD, ACD, ABC và M, N, P lần lượt là trung điểm của các cạnh BD, CD, BC. Chứng minh (IJK) // (BCD) 

Trả lời: ………………………………………

Câu 19:  Cho tứ diện đều S.ABC cạnh bằng 1. Gọi I là trung điểm của AB , M là điểm di động trên đoạn AI. Qua M vẽ mặt phẳng (a) song song với (SIC) . Tính chu vi của thiết diện tạo bởi (a) với tứ diện S.ABC, biết AM = x 

Trả lời: ………………………………………

Câu 20:  Cho tứ diện ABCD có tất cả các cạnh đều bằng 1 và G là trọng tâm của tam giác ABC. Cắt tứ diện bởi mặt phẳng (P) qua G và song song với mặt phẳng (BCD) . Tính diện tích thiết diện thu được (làm tròn kết quả đến hàng phần trăm).

Trả lời: ………………………………………

----------------------------------

----------------------- Còn tiếp -------------------------