Giáo án powerpoint dạy thêm Toán 11 cánh diều Chương 4 Bài 2: Hai đường thẳng song song trong không gian

CHÀO MỪNG CÁC EM 
ĐẾN VỚI BÀI HỌC HÔM NAY!

KHỞI ĐỘNG

+  + Nhóm 1: Cho hai đường thẳng phân biệt a, b và mặt phẳng . Giả sử a // b; b // . Khi đó:

              A. a // ;                                      B. ;            

              C. a cắt ;                                    D. a //  hoặc

+ Nhóm 2: Cho hai đường thẳng phân biệt a, b và mặt phẳng  + Nhóm 2: Cho hai đường thẳng phân biệt a, b và mặt phẳng . Giả sử a // , . Khi đó:

              A. a // b;                                          B. a, b chéo nhau;

BÀI 2. HAI ĐƯỜNG THẲNG 
SONG SONG TRONG KHÔNG GIAN

HỆ THỐNG KIẾN THỨC

1. Vị trí tương đối của hai đường thẳng phân biệt

- Cho hai đường thẳng a và b phân biệt trong không gian. Khi đó chỉ xảy ra một trong các trường hợp sau:

+ Trường hợp 1: Có một mặt phẳng chứa a và b. Khi đó ta nói a và b đồng phẳng.

+ Trường hợp 2: Không có mặt phẳng nào chứa a và b. Khi đó ta nói a và b chéo nhau, hay a chéo với b.

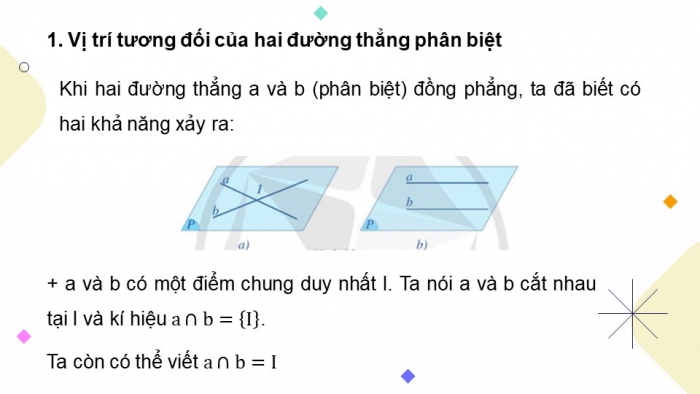
Khi hai đường thẳng a và b (phân biệt) đồng phẳng, ta đã biết có hai khả năng xảy ra:

+ a và b có một điểm chung duy nhất I. Ta nói a và b cắt nhau tại I và kí hiệu .

Ta còn có thể viết

+ a và b không có điểm chung. Ta nói a và b song song với nhau và kí hiệu là a // b

* Nhận biết: Cho hai đường thẳng song song a và b. Có suy nhất một mặt phẳng chứa hai đường thẳng đó, kí hiệu là mp(a, b).

2. Tính chất

a) Định lí 1: Trong không gian, qua một điểm không nằm trên đường thẳng cho trước, có một và chỉ một đường thẳng song song với đường thẳng đã cho.

b) Định lí 2: Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng quy, hoặc đôi một song song với nhau.

* Hệ quả: Nếu hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng (nếu có) sũng song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.

* Hệ quả: Nếu hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng (nếu có) sũng song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.

c) Định lí 3: Trong không gian, hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì song song với nhau.

LUYỆN TẬP, VẬN DỤNG

PHIẾU HỌC TẬP SỐ 1

DẠNG 1: Chứng minh đường thẳng song song hoặc đồng quy

Bài 1. Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng. Gọi O và O’ lần lượt là tâm của hai hình bình hành ABCD và ABEF.

a) Chứng minh OO’ song song với các mặt phẳng (ADF) và (BCE)

b) Gọi G và G’ lần lượt là trọng tâm các tam giác ABD và ABF. Chứng minh GG’ // (DCEF)

Giải

a) Ta có OO’ là đường trung bình của tam giác ACE và tam giác BDF nên: OO’ // CE và OO’ // DF.

Mà  nên OO’ // (BCE) và OO’ // (ADF)