Câu hỏi và bài tập tự luận toán 12 cánh diều

BÀI 1: TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ

(24 câu)

1. NHẬN BIẾT (7 câu)

Câu 1: Cho hàm số  có bảng biến thiên như sau:

a) Hãy xét tính đơn điệu của hàm số.

b) Hãy xác định các điểm cực trị và giá trị cực trị của hàm số đã cho.

Trả lời:

a) Hàm số  đồng biến trên khoảng  và .

    Hàm số  nghịch biến trên khoảng  và .

b) Hàm số đạt cực đại tại điểm , giá trị cực đại là .

    Hàm số đạt cực tiểu tại điểm , giá trị cực tiểu là .

Câu 2: Cho hàm số  có bảng xét dấu của đạo hàm như hình vẽ. Tìm các khoảng đơn điệu của hàm số.

Trả lời:

Hàm số  đồng biến trên khoảng

Hàm số  nghịch biến trên khoảng  và .

Câu 3: Cho hàm số  có đồ thị như hình vẽ dưới đây. Tìm các khoảng đơn điệu của hàm số.

Trả lời:

Hàm số  đồng biến trên khoảng  và .

Hàm số  nghịch biến trên khoảng  và .

Câu 4: Trong các hàm số dưới đây, hàm số nào đồng biến trên .

a)                                                         b)

c)                                              d)

Trả lời:

a) Ta có hàm số  không xác định tại điểm  nên hàm số không đồng biến trên .

b) Ta có tập xác định của hàm số là .

Vậy hàm số đồng biến trên .

c) Ta có tập xác định của hàm số là .

Vậy hàm số nghịch biến trên .

d) Ta có hàm số   không xác định tại điểm  nên hàm số không đồng biến trên .

Câu 5: Cho hàm số  có bảng biến thiên:

a) Tìm khoảng đơn điệu của hàm số.

b) Tìm các điểm cực trị của hàm số.

Trả lời:

a) Hàm số đồng biến trên các khoảng  và .

    Hàm số nghịch biến trên các khoảng .

b) Tại  dù đạo hàm không xác định nhưng hàm số  vẫn xác định và liên tục nên hàm số đạt cực đại tại .

    Tại  thì hàm số  không xác định, vì vậy hàm số không có cực trị tại .

Câu 6: Cho hàm số  xác định, liên tục trên  và có đồ thị của hàm số  là đường cong như hình vẽ bên dưới:

Hãy tìm khoảng đơn điệu của hàm số .

Trả lời:

Hàm số đồng biến trên .

Hàm số nghịch biến trên các khoảng  và .

Câu 7: Cho hàm số  có đạo hàm  xác định, liên tục trên  và  có đồ thị như hình vẽ bên dưới:

Hãy tìm khoảng đơn điệu của hàm số .

Trả lời:

Hàm số đồng biến trên  và .

Hàm số nghịch biến trên  và .

2. THÔNG HIỂU (7 câu)

Câu 1: Tìm khoảng đơn điệu của mỗi hàm số sau:

a) ;                                     b) ;

c)                                                                 d)

Trả lời:

a)

Tập xác định:

Ta có:

Xét

Ta có bảng biến thiên như sau:

Kết luận: Hàm số đồng biến trên các khoảng  và .

                Hàm số nghịch biến trên khoảng .

b)

Tập xác định: .

Ta có:

Xét

Ta có bảng biến thiên như sau:

Kết luận: Hàm số đồng biến trên các khoảng  và .

                Hàm số nghịch biến trên các khoảng  và .

c)   

Tập xác định: .

Ta có: .

Ta có bảng biến thiên như sau:

Kết luận: Hàm số đồng biến trên các khoảng  và .

d)

Tập xác định: .

Ta có:

Xét

Ta có bảng biến thiên như sau:

Kết luận: Hàm số đồng biên trên , nghịch biến trên .

Câu 2: Tìm cực trị của mỗi hàm số sau:

a)                                                   b)

c)                                                                 d)

Trả lời:

a) Tập xác định: .

Ta có: .

Xét

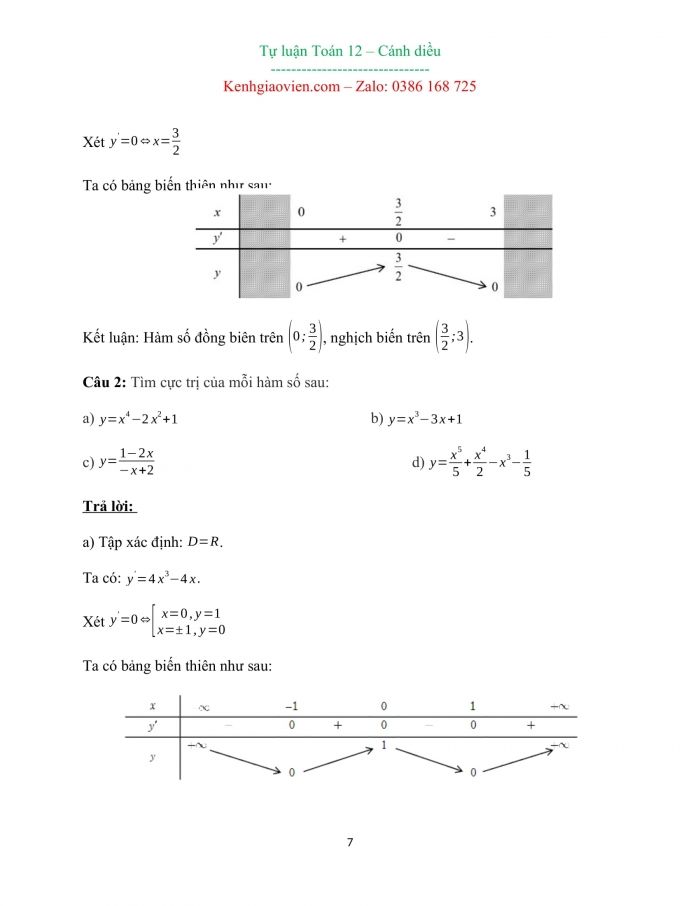
Ta có bảng biến thiên như sau:

Kết luận: Hàm số đạt cực tiểu tại  và , giá trị cực tiểu là .

                  Hàm số đạt cực đại tại , giá trị cực đại là .

b) Tập xác định: .

Ta có: .

Xét

Ta có bảng biến thiên như sau:

Kết luận: Hàm số đạt cực tiểu tại , giá trị cực tiểu là .

               Hàm số đạt cực đại tại , giá trị cực đại là .

c) Tập xác định: .

Ta có: .

Ta có bảng biến thiên như sau:

Kết luận: Hàm số đã cho không có cực trị.

d) Tập xác định: .

Ta có: .

Xét

Ta có bảng biến thiên như sau:

Kết luận: Hàm số đạt cực đại tại điểm , giá trị cực đại là .

                Hàm số đạt cực tiểu tại điểm , giá trị cực tiểu là .

Câu 3: Gọi  là các điểm cực trị của đồ thị hàm số . Tính khoảng cách .

Trả lời:

Tập xác định: .

Ta có:

Xét .

Ta có bảng biến thiên như sau:

Hai điểm cực trị của đồ thị hàm số là .

Do đó: .

Câu 4: Tìm  để hàm số  đồng biến trên tập xác định của nó.

Trả lời:  

Tập xác định: .

Hàm số đồng biến trên tập xác định khi và chỉ khi:

Vậy  

Câu 5: Cho hàm số  liên tục trên  và có đạo hàm , . Xét tính đơn điệu của hàm số đã cho.

Trả lời:

Ta có:

Ta có bảng xét dấu như sau:

Kết luận: Hàm số đồng biến trên .

                Hàm số nghịch biên trên các khoảng  và .

Câu 6: Tìm cực trị của hàm số .

Trả lời:

Tập xác định: .

Ta có: .

Xét

Ta có bảng biến thiên:

Kết luận: Hàm số đạt cực đại tại , giá trị cực đại là .

                Hàm số đạt cực tiểu tại , giá trị cực tiểu là .

Câu 7: Cho hàm số , với . Tìm khoảng đơn điệu của hàm số.

Trả lời:

Tập xác định: .

Ta có:

Xét

Do

Ta có bảng biến thiên như sau:

Kết luận: Hàm số đồng biến trên   và

                Hàm số nghịch biến trên

3. VẬN DỤNG (6 câu)

Câu 1: Cho hàm số . Tìm tất cả các giá trị của  để hàm số đồng biến trên tập xác định.

Trả lời:

Tập xác định: .

Ta có: .

Với , . Khi đó  đổi dấu trên tập xác định khi qua . Vậy  không thỏa mãn.

Với  ta có hàm số đồng biến khi và chỉ khi:

Vậy .

Câu 2: Cho hàm số . Tìm tập hợp tất cả các giá trị của  để hàm số đã cho đồng biến trên khoảng .

Trả lời:

Tập xác định: .

Ta có: .

Để hàm số đồng biến trên  thì .

Đặt .

Mà

Ta có:

Vậy .

Câu 3: Với giá trị nào của tham số  thì hàm số  có cực trị?  

Trả lời:

Tập xác định: .

Ta có: .

Hàm số có cực đại, cực tiểu  có 2 nghiệm phan biệt

Vậy  thì hàm số có cực đại, cực tiểu.

Câu 4: Có bao nhiêu giá trị nguyên của tham số  để đồ thị hàm số  có hai điểm cực trị nằm về hai phía của trục hoành?

Trả lời:

Đồ thị hàm số có hai điểm cực trị nằm về hai phía đối với trục hoành khi và chỉ khi phương trình  có 3 nghiệm phân biệt.

Ta có:

Phương trình có 3 nghiệm phân biệt khi và chỉ khi phương trình (*) có 2 nghiệm phân biệt khác 1.

Do  suy ra .

Vậy có 1 giá trị nguyên của tham số thỏa mãn đề bài.

Câu 5: Cho hàm số  với  là tham số. Tính tổng bình phương tất cả các giá trị của  để hàm số có hai điểm cực trị  thỏa mãn .

Trả lời:

Ta có: .

Để hàm số có hai điểm cực trị thỏa mãn yêu cầu đề bài thì:

Ta có (1)

Mặt khác ta có  (3)

Từ (2) và (3) ta có:

Vì

Vậy tổng bình phương tất cả các giá trị của  thỏa mãn yêu cầu đề bài là:

Câu 6: Tìm tất cả các giá trị của  để hàm số đồng biến trên .

Trả lời:

Ta có: .

Hàm số đồng biến trên

.

Ta thấy giá trị lớn nhất của  bằng  nên

4. VẬN DỤNG CAO (4 câu)

Câu 1: Cho hàm số , có bảng xét dấu  như sau:

Hàm số  đồng biến trên khoảng nào?

Trả lời:

Ta có: .

Hàm số  đồng biến

Vậy hàm số đồng biến trên khoảng  và .

Câu 2: Hàm số  nghịch biến trên khoảng  khi nào?

Trả lời:

Ta có: .

Đặt: , ta có: . Với   thì .

Hàm số nghịch biến trên  khi và chỉ khi hàm số  nghịch biến trên khoảng  

Xét hàm . Ta có:

Ta có bảng biến thiên:

Dựa vào bảng biến thiên, ta có:

Câu 3: Cho hàm số . Tìm  để hàm số đã cho đồng biến trên một khoảng có độ dài lớn hơn 1.

Trả lời:

Ta có: .

Hàm số đồng biến trên khoảng có độ dài lớn hơn 1  có hai nghiệm phân biệt thỏa mãn

Vậy .

Câu 4: Tìm  để đồ thị hàm số  có hai điểm cực trị và hai điểm cực trị đó nằm về cùng một phía đối với trục hoành.

Trả lời:

Tập xác định: .

Ta có:  có .

Để đồ thị hàm số  có hai cực trị thì  đổi dấu hai lần, tức là  có hai nghiệm phân biệt, tương đương

Vì  nên được .

Lúc này, hai nghiệm  của  lần lượt là hoành độ các điểm cực trị của hàm số.

Hai điểm cực trị đó nằm cùng 1 phía đối với trục hoành khi và chỉ khi , tương đương đồ thị hàm số đã cho cắt trục hoành tại đúng một điểm, tức là, phương trình  có duy nhất một nghiệm thực.

Xét  thì phương trình là : phương trình này có đúng một nghiệm thực nên chọn .

Xét  thì phương trình là : phương trình này có đúng một nghiệm thực nên chọn .

Xét  thì phương trình là : phương trình này có ba nghiệm thực nên loại .

Xét  thì phương trình là : phương trình này có đúng một nghiệm thực nên chọn .

Vậy .