Giáo án và PPT đồng bộ Toán 12 chân trời sáng tạo
Toán 12 chân trời sáng tạo. Giáo án word chỉn chu. Giáo án ppt (powerpoint) hấp dẫn, hiện đại. Word và PPT được soạn đồng bộ, thống nhất với nhau. Bộ tài liệu sẽ giúp giáo viên nhẹ nhàng trong giảng dạy. Thầy/cô tham khảo trước để biết chất lượng.
Một số tài liệu quan tâm khác
Phần trình bày nội dung giáo án
Trường:…………..
Giáo viên:
Bộ môn: Toán 12 Chân trời sáng tạo
PHẦN 1: SOẠN GIÁO ÁN WORD TOÁN 12 CHÂN TRỜI SÁNG TẠO
CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
BÀI 1. TÍNH ĐƠN ĐIỆU VÀ CỰC TRỊ CỦA HÀM SỐ
I. MỤC TIÊU:
1. Kiến thức:
Học xong bài này, HS đạt các yêu cầu sau:
Nhận biết được tính đồng biến, nghịch biến của một hàm số trên một khoảng dựa vào dấu của đạo hàm cấp một của nó.
Thể hiện được tính đồng biến, nghịch biến của hàm số trong bảng biến thiên.
Nhận biết được tính đơn điệu, điểm cực trị, giá trị cực trị của hàm số thông qua bảng biến thiên hoặc thông qua hình ảnh hình học của đồ thị hàm số.
Vận dụng đạo hàm và tính đơn điệu của hàm số để giải quyết một số vấn đề liên quan đến thực tiễn.
2. Năng lực
Năng lực chung:
Năng lực tự chủ và tự học trong tìm tòi khám phá.
Năng lực giao tiếp và hợp tác trong trình bày, thảo luận và làm việc nhóm.
Năng lực giải quyết vấn đề và sáng tạo trong thực hành, vận dụng.
Năng lực riêng: tư duy và lập luận toán học, giao tiếp toán học; mô hình hóa toán học; giải quyết vấn đề toán học.
Tư duy và lập luận toán học: Lập luận, phân tích, so sánh để xác định được khái niệm tính đồng biến, nghịch biến của hàm số, từ đó xác định được các điểm cực trị và giá trị cực trị của hàm số.
Mô hình hóa toán học: Thể hiện được tính đồng biến, nghịch biến của hàm số trong bảng biến thiên dựa vào dấu của đạo hàm.
Giải quyết vấn đề toán học: sử dụng dấu của đạo hàm để xác định tính đồng biến, nghịch biến, xác định cực trị của hàm số.
Giao tiếp toán học: Đọc hiểu thông tin toán học từ đồ thị, bảng biến thiên.
Sử dụng công cụ, phương tiện học toán: sử dụng máy tính cầm tay để tính giá trị cực trị của hàm số.
3. Phẩm chất
Tích cực thực hiện nhiệm vụ khám phá, thực hành, vận dụng.
Có tinh thần trách nhiệm trong việc thực hiện nhiệm vụ được giao.
Khách quan, công bằng, đánh giá chính xác bài làm của nhóm mình và nhóm bạn.
Tự tin trong việc tính toán; giải quyết bài tập chính xác.
II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU
1 - GV: SGK, SGV, Tài liệu giảng dạy, giáo án PPT, PBT (ghi đề bài cho các hoạt động trên lớp), các hình ảnh liên quan đến nội dung bài học,...
2 - HS:
- SGK, SBT, vở ghi, giấy nháp, đồ dùng học tập (bút, thước...), bảng nhóm, bút viết bảng nhóm.
III. TIẾN TRÌNH DẠY HỌC
A. HOẠT ĐỘNG KHỞI ĐỘNG (MỞ ĐẦU)
a) Mục tiêu:
- Tạo hứng thú, thu hút HS tìm hiểu nội dung bài học.
b) Nội dung: HS đọc bài toán mở đầu và thực hiện bài toán dưới sự dẫn dắt của GV (HS chưa cần giải bài toán ngay).
c) Sản phẩm: HS nhận biết được các thông tin trong bài toán và dự đoán câu trả lời cho câu hỏi mở đầu theo ý kiến cá nhân.
d) Tổ chức thực hiện:
Bước 1: Chuyển giao nhiệm vụ:
- GV chiếu Slide dẫn dắt và yêu cầu HS thảo luận và nêu dự đoán về câu hỏi mở đầu (chưa cần HS giải):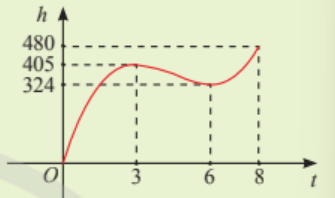 
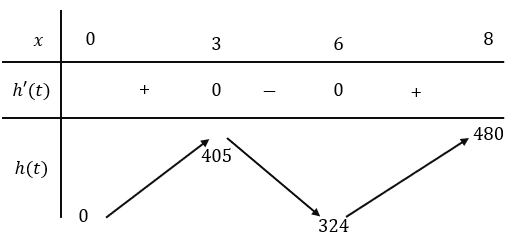
Trong 8 phút đầu kể từ khi xuất phát, độ cao h (tính bằng mét) của khinh khí cầu vào thời điểm t phút được cho bởi công thức ht=6t3-81t2+324t. Đồ thị của hàm số h(t) được biểu diễn trong hình bên.
Trong khoảng thời gian nào khinh khí cầu tăng dần độ cao, giảm dần độ cao?
Độ cao của khinh khí cầu vào các thời điểm 3 phút và 6 phút sau khi xuất phát có gì đặc biệt?
Bước 2: Thực hiện nhiệm vụ: HS quan sát và chú ý lắng nghe, thảo luận nhóm và thực hiện yêu cầu theo dẫn dắt của GV.
Bước 3: Báo cáo, thảo luận: GV gọi đại diện một số thành viên nhóm HS trả lời, HS khác nhận xét, bổ sung.
Bước 4: Kết luận, nhận định: GV ghi nhận câu trả lời của HS, trên cơ sở đó dẫn dắt HS vào tìm hiểu bài học mới: “Ở lớp dưới chúng ta đã học về tính đồng biến và nghịch biến của một hàm số. Trong bài học ngày hôm nay, chúng ta sẽ học cách xét tính đơn điệu của hàm số dựa vào dấu của đạo hàm và cách tìm điểm cực trị, giá trị cực trị của hàm số.”
B. HÌNH THÀNH KIẾN THỨC MỚI
Hoạt động 1: Tính đơn điệu của hàm số
a) Mục tiêu:
- HS nhận biết được tính đồng biến, nghịch biến của một hàm số trên một khoảng dựa vào dấu của đạo hàm cấp một của nó.
- HS thể hiện được tính đồng biến, nghịch biến của hàm số trong bảng biến thiên.
b) Nội dung:
- HS đọc SGK, nghe giảng, thực hiện các nhiệm vụ được giao, suy nghĩ trả lời câu hỏi, thực hiện HĐKP1; Thực hành 1, 2, 3, Vận dụng 1 và các Ví dụ.
c) Sản phẩm: HS hình thành được kiến thức bài học, câu trả lời của HS cho các câu hỏi, HS nhận biết được tính đồng biến, nghịch biến của hàm số, thể hiện được tính đơn điệu của hàm số trong bảng biến thiên.
d) Tổ chức thực hiện:
HĐ CỦA GV VÀ HS | SẢN PHẨM DỰ KIẾN |
Bước 1: Chuyển giao nhiệm vụ: NV1: Nhắc lại về tính đồng biến, nghịch biến của hàm số - GV yêu cầu học sinh nhắc lại về tính đồng biến, nghịch biến của hàm số. + Hàm số có tính chất như thế nào được gọi là đồng biến, nghịch biến?
+ Hàm số đồng biến có dạng đồ thị như thế nào? Hàm số nghịch biến có dạng đồ thị như thế nào?
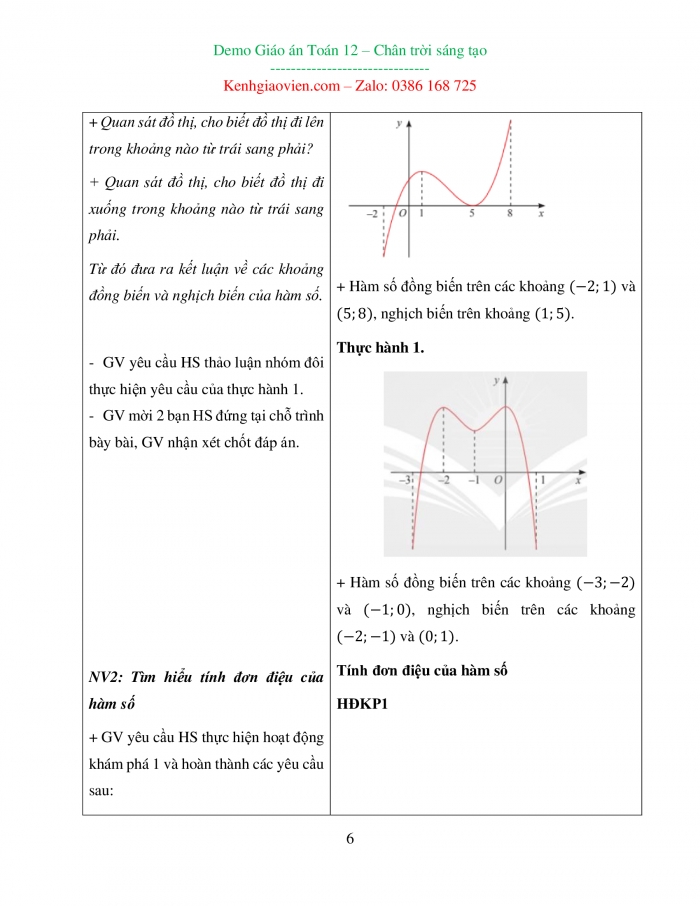
+ Quan sát đồ thị, cho biết đồ thị đi lên trong khoảng nào từ trái sang phải? + Quan sát đồ thị, cho biết đồ thị đi xuống trong khoảng nào từ trái sang phải. Từ đó đưa ra kết luận về các khoảng đồng biến và nghịch biến của hàm số.
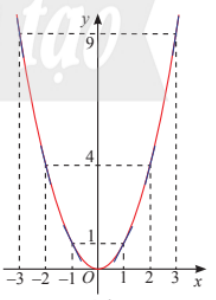
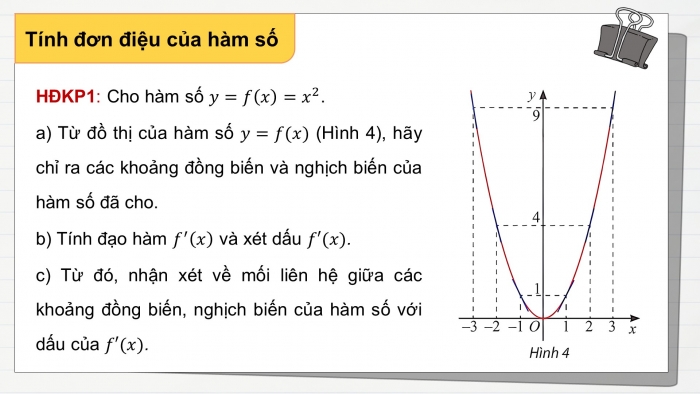
NV2: Tìm hiểu tính đơn điệu của hàm số + GV yêu cầu HS thực hiện hoạt động khám phá 1 và hoàn thành các yêu cầu sau: Cho hàm số y=fx=x2.
a) Từ đồ thị của hàm số y=f(x), hãy chỉ ra các khoảng đồng biến và nghịch biến của hàm số đã cho. b) Tính đạo hàm f'x và xét dấu f'(x).
c) Từ đó, nhận xét về mối liên hệ giữa các khoảng đồng biến, nghịch biến của hàm số với dấu của f'(x). - GV mời 3 HS lên bảng trình bày. - GV nhận xét, kết luận về tính đơn điệu của hàm số.
- GV chia lớp thành 4 nhóm để thảo luận và thực hiện phần Thực hành 2. + Nhóm 1 và 2, thực hiện câu a). + Nhóm 3 và 4, thực hiên câu b). + Các nhóm thực hiện trao đổi, thống nhất đáp án trong 6 - 8 phút.
a) fx=x3-6x2+9x; b) gx=1x. + Sau thời gian thảo luận, GV mời đại diện từng nhóm lên thực hiện bài giải của nhóm mình. + HS dưới lớp quan sát, thực hiện bài làm vào vở cá nhân. + GV quan sát, nhận xét bài làm của HS và rút ra kinh nghiệm làm bài cho HS.
+ Tính f'(x) của hàm số trên tập xác định. + Giá trị của cos x nằm trong khoảng nào? Từ đó xét dấu của f'(x).
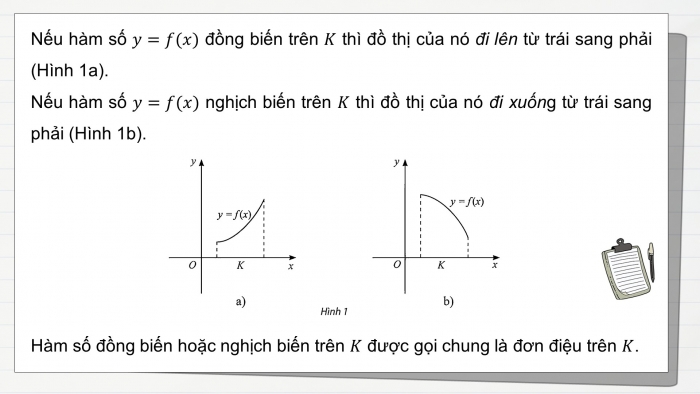
Bước 2: Thực hiện nhiệm vụ: - HĐ cá nhân: HS suy nghĩ, hoàn thành vở. Cả lớp chú ý thực hiện các yêu cầu của GV, chú ý bài làm các bạn và nhận xét. - GV: quan sát và trợ giúp HS. Bước 3: Báo cáo, thảo luận: - HS trả lời trình bày miệng/ trình bày bảng, cả lớp nhận xét, GV đánh giá, dẫn dắt, chốt lại kiến thức. Bước 4: Kết luận, nhận định: GV tổng quát lưu ý lại kiến thức trọng tâm + Nhắc lại về tính đồng biến, nghịch biến của hàm số. + Tính đơn điệu của hàm số. | 1. Tính đơn điệu của hàm số Nhắc lại về tính đồng biến, nghịch biến của hàm số Kí hiệu K là khoảng hoặc đoạn hoặc nửa khoảng. Giả sử hàm số y=f(x) xác định trên K. Hàm số y=f(x) gọi là đồng biến (tăng) trên K nếu với mọi x1,x2 thuộc K mà x1<x2 thì f(x1)<f(x2). Hàm số y=f(x) gọi là nghịch biến (giảm) trên K nếu với mọi x1,x2 thuộc K mà x1<x2 thì f(x1)>f(x2). Nếu hàm số y=f(x) đồng biến trên K thì đồ thị của nó đi lên từ trái sang phải.
Nếu hàm số y=f(x) nghịch biến trên K thì đồ thị của nó đi xuống từ trái sang phải.
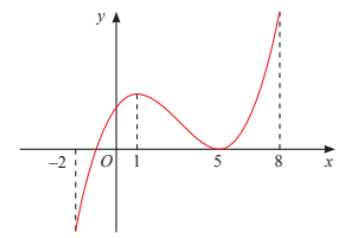
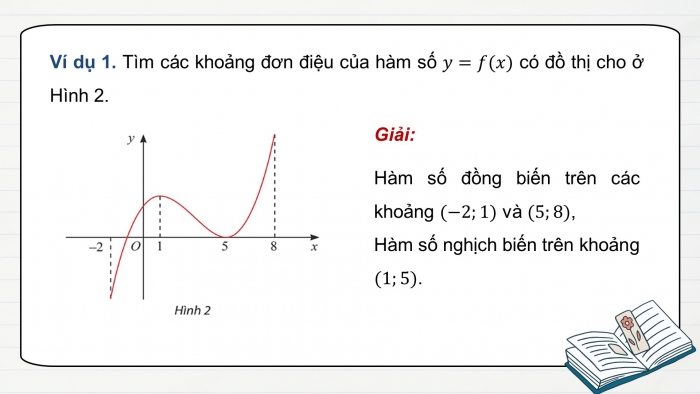
Ví dụ 1: Tìm các khoảng đơn điệu của hàm số y=f(x) có đồ thị cho ở Hình 2.
+ Hàm số đồng biến trên các khoảng (-2;1) và (5;8), nghịch biến trên khoảng (1;5). Thực hành 1.
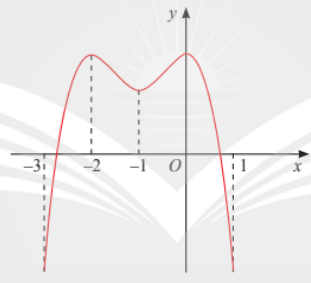
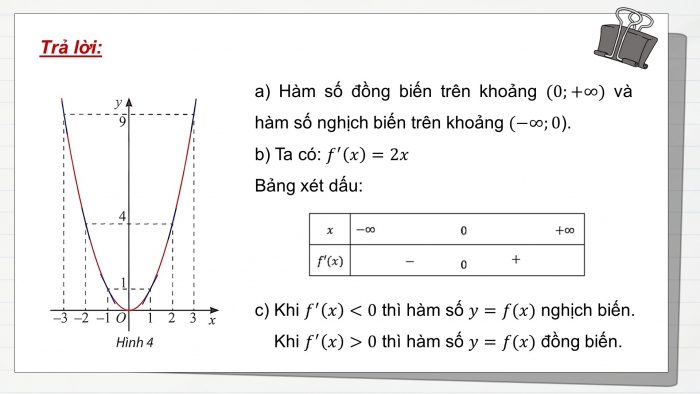
+ Hàm số đồng biến trên các khoảng (-3;-2) và (-1;0), nghịch biến trên các khoảng (-2;-1) và (0;1). Tính đơn điệu của hàm số HĐKP1
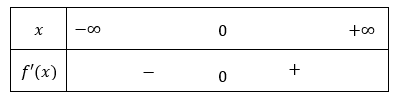
a) Hàm số đồng biến trên khoảng (0;+∞) và hàm số nghịch biến trên khoảng (-∞;0). b) Ta có: f'x=2x Bảng xét dấu:
c) Khi f'x<0 thì hàm số y=f(x) nghịch biến. Khi f'x>0 thì hàm số y=f(x) đồng biến.
Kết luận Cho hàm số y=f(x) có đạo hàm trên K. Nếu f'x>0 với mọi x thuộc K thì hàm số y=f(x) đồng biến trên K. Nếu f'x<0 với mọi x thuộc K thì hàm số y=f(x) nghịch biến trên K. Ví dụ 2 (SGK – tr.8) Hướng dẫn giải – SGK – tr.8
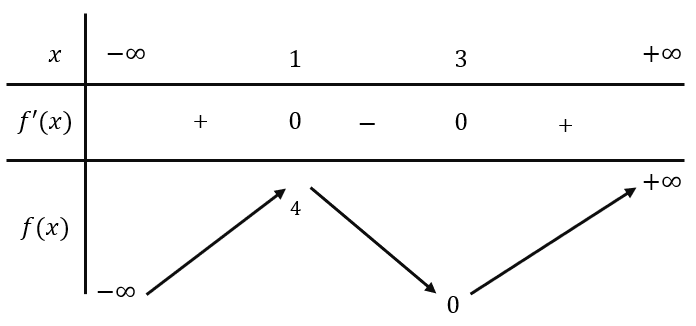
Chú ý: Khi xét tinh đơn điệu của hàm số mà chưa cho khoảng K, ta hiểu xét tính đơn điệu của hàm số đó trên tập xác định của nó. Các bước thực hiện Để xét tính đơn điệu của hàm số y=f(x), ta thực hiện các bước sau: Bước 1: Tìm tập xác định D của hàm số. Bước 2: Tính đạo hàm f'(x) của hàm số. Tìm các điểm x thuộc D mà tại đó đạo hàm f'(x) bằng 0 hoặc đạo hàm không tồn tại. Bước 3: Xét dấu f'(x) và lập bảng biến thiên. Bước 4: Nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số. Ví dụ 3 (SGK – Tr.8) Hướng dẫn giải – SGK – tr.8-9. Chú ý: a) Nếu hàm số y=f(x) có đạo hàm trên K, f'x≥0 với mọi x∈K và f'x=0 chỉ tại một số hữu hạn điểm thì hàm số đồng biến trên K. b) Nếu hàm số y=f(x) có đạo hàm trên K, f'x≤0 với mọi x∈K và f'x=0 chỉ tại một số hữu hạn điểm thì hàm số nghịch biến trên K. c) Nếu f'x=0 với mọi x∈K thì hàm số không đổi trên K. Thực hành 2. a) Tập xác định: D=R Ta có: f'x=3x2-12x+9 f'x=0⟺[x=1 x=3 Bảng biến thiên:
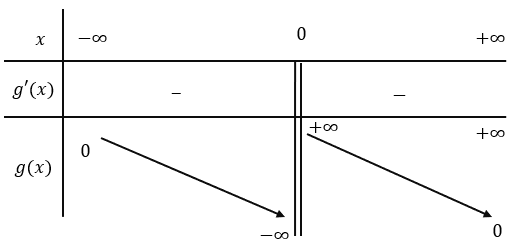
Hàm số đồng biến trên các khoảng -∞;1 và 3;+∞. Hàm số nghịch biến trên khoảng (1;3). b) Tập xác định: D=R\{0}. Ta có: g'x=-1x2<0 Bảng biến thiên:
Hàm số nghịch biến trên các khoảng (-∞;0) và (0;+∞). Thực hành 3. Tập xác định: D=R. Ta có: f'x=3-cos x Vì x≤1 nên f'x>0 Vậy hàm số đồng biến trên R.
Vận dụng 1. Ta có: h't=18t2-162t+324 h't=0⇔[t=3 t=6 Bảng biến thiên:
Trong khoảng thời gian (0;3) và (6;8) khinh khí cầu tăng dần độ cao, trong khoảng thời gian (3;6) khinh khí cầu giảm dần độ cao. |
-----------Còn tiếp-----------
PHẦN 2: BÀI GIẢNG POWERPOINT TOÁN 12 CHÂN TRỜI SÁNG TẠO
CHÀO MỪNG TẤT CẢ CÁC EM ĐẾN VỚI TIẾT HỌC HÔM NAY!
BÀI 1: TÍNH ĐƠN ĐIỆU VÀ CỰC TRỊ CỦA HÀM SỐ
CHÀO MỪNG TẤT CẢ HỌC SINH LỚP 12 ĐẾN VỚI BÀI HỌC NGÀY HÔM NAY
KHỞI ĐỘNG
- GV chiếu bài tập trắc nghiệm nhanh, HS nhanh chóng củng cố kiến thức và chuyển sang nội dung bài học mới.
HOẠT ĐỘNG HÌNH THÀNH KIẾN THỨC
1. TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ
HS hoàn thành thực hành 1 trang 7 toán 12 tập 1 ctst
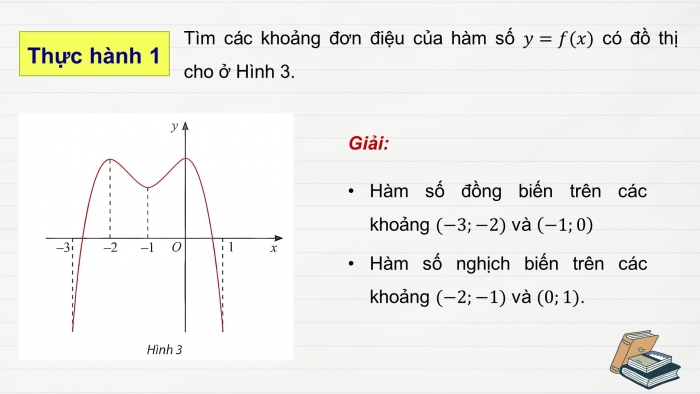
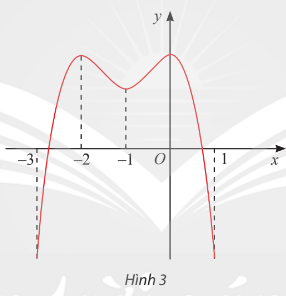
Tìm các khoảng đơn điệu của hàm số 
có đồ thị cho ở Hình 3.
Bài giải:
Hàm số đồng biến trên các khoảng 
và 
, nghịch biến trên khoảng 
và 
.
lý thuyết:
Cho hàm số 
có đạo hàm trên K.
Nếu 
với mọi x thuộc K thì hàm số 
đồng biến trên K.
Nếu 
với mọi x thuộc K thì hàm số 
nghịch biến trên K.
2. CỰC TRỊ CỦA HÀM SỐ
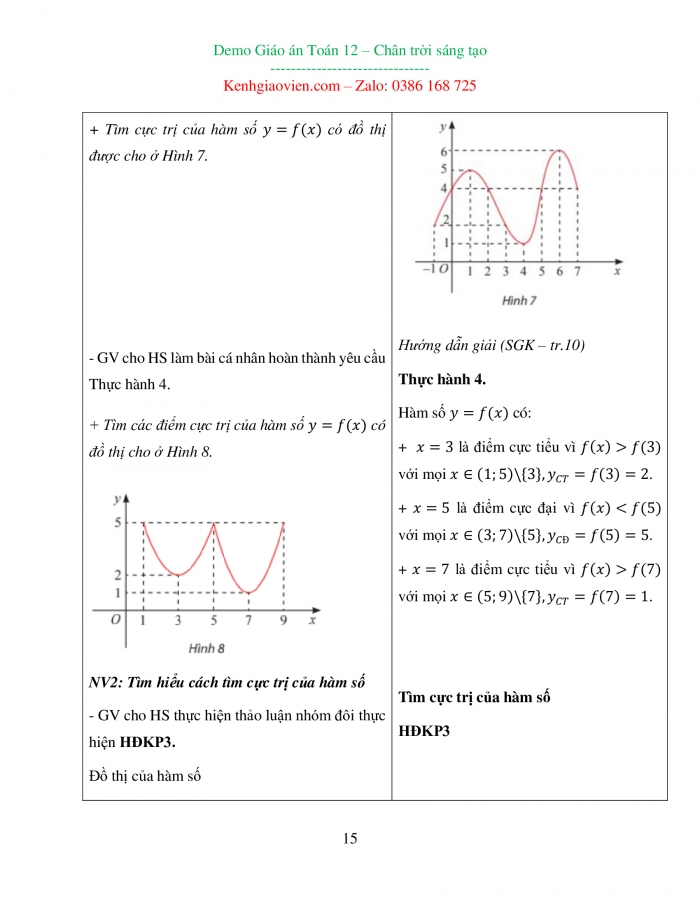
HS hoàn thành hoạt động 2 trang 10 toán 12 tập 1 ctst
Quan sát đồ thị của hàm số 
trong Hình 5.
a) Tìm khoảng 
chứa điểm 
mà trên đó 
với mọi 
.
b) Tìm khoảng 
chứa điểm 
mà trên đó 
với mọi 
.
c) Tồn tại hay không khoảng 
chứa điểm 
mà trên đó 
với mọi 
hoặc 
với mọi 
.
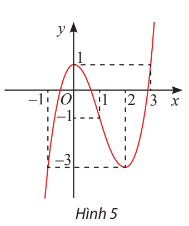
Bài giải:
a) Trên khoảng 
với mọi 
.
b) Trên khoảng 
với mọi 
.
c) Không tồn tại khoảng 
chứa điểm 
mà trên đó 
với mọi 
hoặc 
với mọi 
lý thuyết:
Cho hàm số 
xác định trên tập hợp 
và 
.
- Nếu tồn tại một khoảng 
chứa điểm 
và 
sao\ cho
với mọi 
thì 
được gọi là một điểm cục đại, 
được gọi là giá trị cụcc đại của hàm số 
, kí hiệu 
- Nếu tồn tại một khoảng 
chứa điểm 
và 
sao cho 
với mọi 
, thì 
được gọi là một điểm cực tiểu, 
được gọi là giá trị cực tiểu của hàm số 
, kí hiệu 
lý thuyết:
Cho hàm số 
liên tục trên khoảng (a ; b) chứa điểm 
và có đạo hàm trên các khoảng 
và 
. Khi đó:
- Nếu 
với mọi 
và 
với mọi 
thì hàm số 
đạt cực tiểu tại điểm 
;
- Nếu 
với mọi 
và 
với mọi 
thì hàm số 
đạt cực đại tại điểm 
.
3. BÀI TẬP CUỐI SÁCH GIÁO KHOA
Bài 1 trang 13 toán 12 tập 1 ctst
Tìm các khoảng đơn điệu và cực trị của các hàm số có đồ thị cho ở Hình 11.
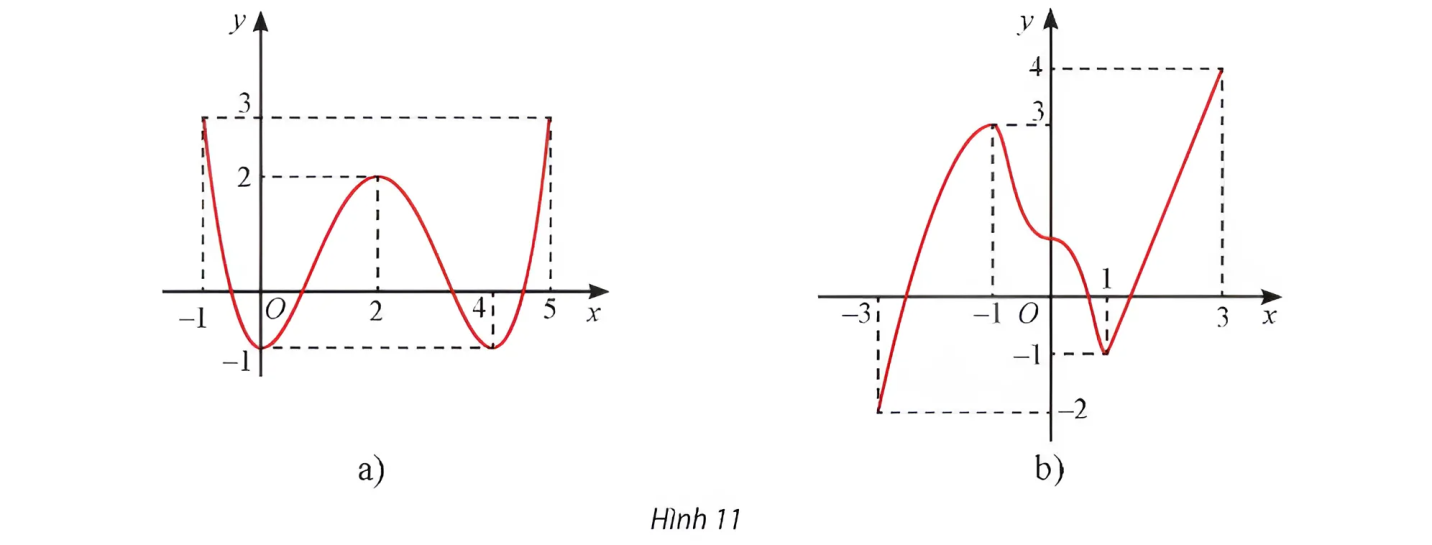
Bài giải:
a) Hàm số đồng biến trên các khoảng 
và
nghịch biến trên các khoảng 
và 
Hàm số đạt cực tiểu tại 
và 
, giá trị cực tiểu là 
; hàm số đạt cực đại tại 
, giá trị cực đại là
.
b) Hàm số đồng biến trên các khoảng 
và 
; nghịch biến trên các khoảng 
.
Hàm số đạt cực tiểu tại 
, giá trị cực tiểu là 
; hàm số đạt cực đại tại 
, giá trị cực đại là 
.
Bài 2 trang 13 toán 12 tập 1 ctst
Xét tính đơn điệu và tìm điểm cực trị của các hàm số sau:
a) 
;
b) 
.
Bài giải:
a) Xét hàm số 
Tập xác định: 
Ta có: 
hoặc 
Bảng biến thiên:
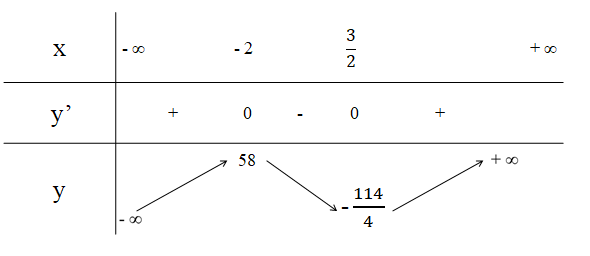
Hàm số 
đồng biến trên các khoảng 
và 
; hàm số nghịch biến trên các khoảng 
Hàm số đạt cực tiểu tại 
, giá trị cực tiểu là
; hàm số cực đại tại
, giá trị cực đại là 
.
b) Xét hàm số 
.
Tập xác định: 
Ta có: 
= 
= 
= 
Vì 
với mọi 
nên 
Bảng biến thiên:
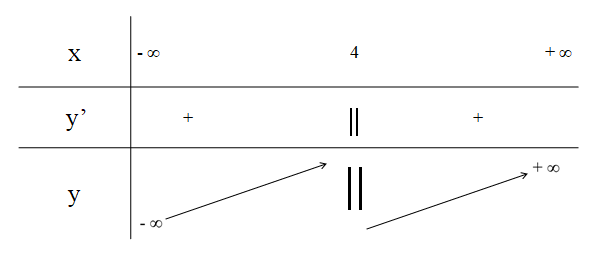
Hàm số 
đồng biến trên các khoảng 
Hàm số không có cực trị.
-----------Còn tiếp-----------
PHẦN 3: TÀI LIỆU THAM KHẢO ĐƯỢC TẶNG KÈM
1. TRỌN BỘ TRẮC NGHIỆM TOÁN 12 CHÂN TRỜI SÁNG TẠO
Bộ trắc nghiệm toán 12 chân trời sáng tạo tổng hợp câu hỏi trắc nghiệm: nhận biết, thông hiểu, vận dụng, vận dụng cao và trắc nghiệm Đ/S
CHƯƠNG 1. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
BÀI 1: TÍNH ĐƠN ĐIỆU VÀ CỰC TRỊ CỦA HÀM SỐ
(30 câu)
A. TRẮC NGHIỆM
1. NHẬN BIẾT (10 câu)
Câu 1: Cho hàm số y=f(x) có đạo hàm trên khoảng (a;b). Chọn khẳng định đúng trong các khẳng định sau:
A. Nếu f'x>0 với mọi x thuộc (a;b) thì hàm số f(x) đồng biến trên (a;b).
B. Nếu f'x>0 với mọi x thuộc (a;b) thì hàm số f(x) nghịch biến trên (a;b).
C. Nếu f'x<0 với mọi x thuộc (a;b) thì hàm số f(x) đồng biến trên (a;b).
D. Nếu f'x=0 với mọi x thuộc (a;b) thì hàm số f(x) đồng biến trên (a;b).
Câu 2: Cho hàm số y=f(x) có bảng xét dấu đạo hàm f'(x) như sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A. (3;+∞). | B. (-3;3). | C. (-∞;-3). | D. (-∞;+∞). |
Câu 3: Cho hàm số bấc ba y=f(x) có đồ thị là đường cong trong hình bên
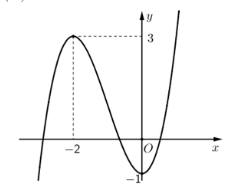
Giá trị cực tiểu của hàm số đã cho là:
A. -2. | B. 0. | C. -1. | D. 3. |
Câu 4: Cho hàm số y=f(x) có bảng xét dấu của đạo hàm như sau:
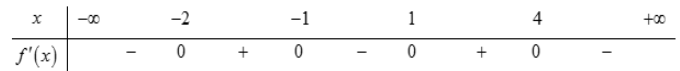
Số điểm cực tiểu của hàm số đã cho là:
A. 4. | B. 3. | C. 2. | D. 1. |
Câu 5: Cho hàm số y=f(x) có bảng biến thiên như sau:
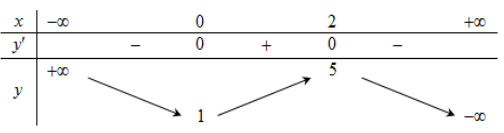
Giá trị cực đại của hàm số đã cho bằng:
A. 0. | B. 5. | C. 2. | D. 1. |
Câu 6: Cho hàm số f(x) đồng biến trên tập số thực R, mệnh đề nào sau đây là đúng?
A. Với mọi x1>x2∈R thì fx1<f(x2).
B. Với mọi x1,x2∈R thì fx1>f(x2).
C. Với mọi x1,x2∈R thì fx1<f(x2).
D. Với mọi x1<x2∈R thì fx1<f(x2).
Câu 7: Cho hàm số fx có đạo hàm trên R là f'x=x-1. Hàm số đã cho đồng biến trên khoảng:
A. (1;+∞). | B. (-∞;+∞). | C. (0;1). | D. (-∞;1). |
Câu 8: Cho hàm số có đồ thị như hình vẽ. Giá trị cực đại của hàm số bằng:
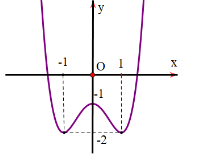
A. -2. | B. -1. | C. 1. | D. 0. |
Câu 9: Cho hàm số f(x) xác định trên R và có đồ thị cảu hàm số f'(x) như hình vẽ. Hàm số f(x) có bao nhiêu điểm cực trị?
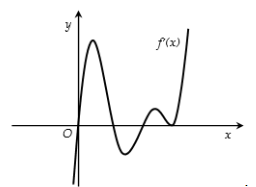
A. 2. | B. 4. | C. 3. | D. 1. |
Câu 10: Cho hàm số y=f(x) có đồ thị như hình vẽ bên. Hàm số y=f(x) nghịch biến trên khoảng nào sau đây?
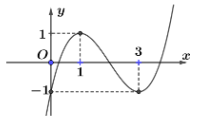
A. (0;3). | B. (1;3). | C. (-1;3). | D. (3;+∞). |
2. THÔNG HIỂU (10 CÂU)
Câu 1: Cho hàm số y=x3-3x2. Chọn khẳng định đúng trong các khẳng định sau:
A. Hàm số nghịch biến trên khoảng (0;2).
B. Hàm số nghịch biến trên khoảng (2;+∞).
C. Hàm số nghịch biến trên khoảng (-∞;+∞).
D. Hàm số nghịch biến trên khoảng (-∞;0)
Câu 2: Hàm số nào sau đây đồng biế trên R?
A. y=x-1x+1. | B. y=-x3-3x+1. |
C. y=2x3+3x+1. | D. y=x4+2x2. |
------Còn tiếp-----------
2. TRỌN BỘ ĐỀ THI TOÁN 12 CHÂN TRỜI SÁNG TẠO
Bộ đề Toán 12 Chân trời sáng tạo biên soạn đầy đủ gồm: đề thi + hướng dẫn chấm điểm, bảng năng lực và cấp độ tư duy, bảng đặc tả kĩ thuật
SỞ GD & ĐT ………………. | Chữ kí GT1: ........................... |
TRƯỜNG THPT………………. | Chữ kí GT2: ........................... |
ĐỀ KIỂM TRA GIỮA HỌC KÌ I
TOÁN 12 – CHÂN TRỜI SÁNG TẠO
NĂM HỌC: 2024 - 2025
Thời gian làm bài: 90 phút (Không kể thời gian phát đề)
Họ và tên: …………………………………… Lớp: ……………….. Số báo danh: …………………………….……Phòng KT:………….. | Mã phách |
"
Điểm bằng số
| Điểm bằng chữ | Chữ ký của GK1 | Chữ ký của GK2 | Mã phách |
PHẦN I. Câu trắc nghiệm nhiều phương án lực chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chọn một phương án.
Câu 1. Cho hàm số 
xác định và liên tục trên 
, có bảng biến thiên như sau:
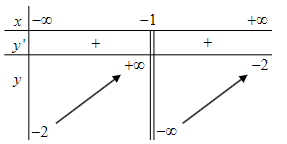
Khẳng định nào sau đây đúng?
A. Đồ thị hàm số có ba đường tiệm cận.
B. Đồ thị hàm số có duy nhất một đường tiệm cận.
C. Đồ thị hàm số có tiệm cận đứng là đường thẳng 
và tiệm cận ngang là đường thẳng 
.
D. Đồ thị hàm số có tiệm cận đứng là đường thẳng 
và tiệm cận ngang là đường thẳng 
.
Câu 2. Hàm số nào sau đây có cực trị?
A. 
B. 
.
C. 
D. 
.
Câu 3. Hàm số 
có đồ thị như hình vẽ.
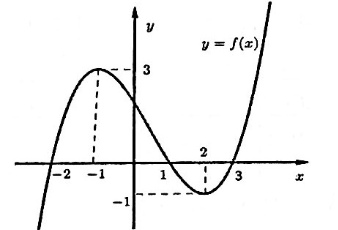
Mệnh đề nào sau đây sai?
A. Hàm số đã cho nghịch biến trên khoảng 
.
B. Hàm số đã cho nghịch biến trên khoảng 
.
C. Hàm số đã cho đồng biến trên khoảng 
.
D. Hàm số đã cho đồng biến trên khoảng 
.
Câu 4. Cho hàm số 
có cực trị tại hai điểm 
. Giá trị của biểu thức 
bằng:
A. 
B. 
.
C. 
.
D. 
.
Câu 5. Cho hàm số 
liên tục trên 
và có đồ thị như hình vẽ bên. Gọi 
và 
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên 
. Giá trị của 
bằng:
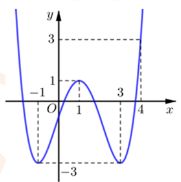
A. 
.
B. 
.
C. 
.
D. 
.
Câu 6. Biết 
là các điểm cực trị của đồ thị hàm số 
. Tính giá trị của hàm số tại 
.
A. 
.
B. 
C. 
.
D. 
.
Câu 7. Đồ thị hàm số 
có đường tiệm cận đứng là 
. Giá trị của 
bằng:
A. 
.
B. 
.
C. 
.
D. 
.
Câu 8. Biết rằng hàm số 
đạt giá trị lớn nhất trên khoảng 
tại 
. Tính 
.
A. 
.
B. 
.
C. 
.
D. 
.
------Còn tiếp-----------
Hệ thống có đầy đủ các tài liệu:
- Giáo án word (350k)
- Giáo án Powerpoint (400k)
- Trắc nghiệm theo cấu trúc mới (200k)
- Đề thi cấu trúc mới: ma trận, đáp án, thang điểm..(200k)
- Phiếu trắc nghiệm câu trả lời ngắn (200k)
- Trắc nghiệm đúng sai (200k)
- Lý thuyết bài học và kiến thức trọng tâm (200k)
- File word giải bài tập sgk (150k)
- Phiếu bài tập để học sinh luyện kiến thức (200k)
- .....
Nâng cấp lên VIP đê tải tất cả ở tài liệu trên
- Phí nâng cấp VIP: 900k
=> Chỉ gửi 500k. Tải về dùng thực tế. Nếu hài lòng, 1 ngày sau mới gửi phí còn lại
Cách tải hoặc nâng cấp:
- Bước 1: Chuyển phí vào STK: 1214136868686 - cty Fidutech - MB(QR)
- Bước 2: Nhắn tin tới Zalo Fidutech - nhấn vào đây để thông báo và nhận tài liệu
=> Nội dung chuyển phí: Nang cap tai khoan
=> Giáo án toán 12 chân trời sáng tạo
Xem thêm tài liệu:
Từ khóa: Giáo án và PPT đồng bộ toán 12 chân trời sáng tạo, soạn giáo án word và powerpoint Toán 12 chân trời, soạn toán 12 chân trời sáng tạo
Tài liệu giảng dạy môn Toán THPT