Trắc nghiệm toán 12 chân trời sáng tạo
Trắc nghiệm Toán 12 chân trời sáng tạo. Trắc nghiệm bao gồm: trắc nghiệm Nhận biết, thông hiểu, vận dụng, vận dụng cao và trắc nghiệm Đúng/Sai . Tài liệu này sẽ hữu ích trong việc kiểm tra bài cũ, phiếu học tập, đề thi, kiểm tra... Trắc nghiệm có file word tải về và đáp án. Chúc quý thầy cô dạy tốt môn Toán 12 chân trời.
Click vào ảnh dưới đây để xem giáo án rõ












Một số tài liệu quan tâm khác
Phần trình bày nội dung giáo án
CHƯƠNG 1. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
BÀI 1: TÍNH ĐƠN ĐIỆU VÀ CỰC TRỊ CỦA HÀM SỐ
(30 câu)
A. TRẮC NGHIỆM NHIỀU ĐÁP ÁN LỰA CHỌN
1. NHẬN BIẾT (10 câu)
Câu 1: Cho hàm số ![]() có đạo hàm trên khoảng
có đạo hàm trên khoảng ![]() . Chọn khẳng định đúng trong các khẳng định sau:
. Chọn khẳng định đúng trong các khẳng định sau:
A. Nếu ![]() với mọi
với mọi ![]() thuộc
thuộc ![]() thì hàm số
thì hàm số ![]() đồng biến trên
đồng biến trên ![]() .
.
B. Nếu ![]() với mọi
với mọi ![]() thuộc
thuộc ![]() thì hàm số
thì hàm số ![]() nghịch biến trên
nghịch biến trên ![]() .
.
C. Nếu ![]() với mọi
với mọi ![]() thuộc
thuộc ![]() thì hàm số
thì hàm số ![]() đồng biến trên
đồng biến trên ![]() .
.
D. Nếu ![]() với mọi
với mọi ![]() thuộc
thuộc ![]() thì hàm số
thì hàm số ![]() đồng biến trên
đồng biến trên ![]() .
.
Câu 2: Cho hàm số ![]() có bảng xét dấu đạo hàm
có bảng xét dấu đạo hàm ![]() như sau:
như sau:

Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A. ![]()
B. ![]()
C. ![]()
D. ![]() .
.
Câu 3: Cho hàm số bấc ba ![]() có đồ thị là đường cong trong hình bên
có đồ thị là đường cong trong hình bên
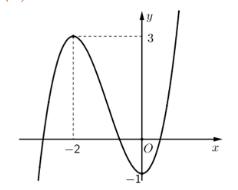
Giá trị cực tiểu của hàm số đã cho là:
A. ![]()
B. ![]()
C. ![]() .
.
D. ![]() .
.
Câu 4: Cho hàm số ![]() có bảng xét dấu của đạo hàm như sau:
có bảng xét dấu của đạo hàm như sau:

Số điểm cực tiểu của hàm số đã cho là:
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Câu 5: Cho hàm số ![]() có bảng biến thiên như sau:
có bảng biến thiên như sau:
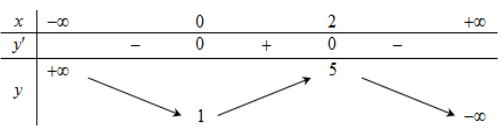
Giá trị cực đại của hàm số đã cho bằng:
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Câu 6: Cho hàm số ![]() đồng biến trên tập số thực
đồng biến trên tập số thực ![]() , mệnh đề nào sau đây là đúng?
, mệnh đề nào sau đây là đúng?
A. Với mọi ![]() thì
thì ![]() .
.
B. Với mọi ![]() thì
thì ![]() .
.
C. Với mọi ![]() thì
thì ![]() .
.
D. Với mọi ![]() thì
thì ![]() .
.
Câu 7: Cho hàm số ![]() có đạo hàm trên
có đạo hàm trên ![]() là
là ![]() . Hàm số đã cho đồng biến trên khoảng:
. Hàm số đã cho đồng biến trên khoảng:
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Câu 8: Cho hàm số có đồ thị như hình vẽ. Giá trị cực đại của hàm số bằng:
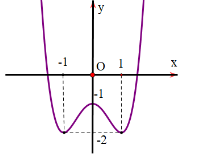
A. ![]() .
.
B. ![]() .
.
C. 1.
D. ![]() .
.
Câu 9: Cho hàm số ![]() xác định trên
xác định trên ![]() và có đồ thị cảu hàm số
và có đồ thị cảu hàm số ![]() như hình vẽ. Hàm số
như hình vẽ. Hàm số ![]() có bao nhiêu điểm cực trị?
có bao nhiêu điểm cực trị?
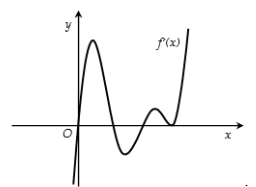
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Câu 10: Cho hàm số ![]() có đồ thị như hình vẽ bên. Hàm số
có đồ thị như hình vẽ bên. Hàm số ![]() nghịch biến trên khoảng nào sau đây?
nghịch biến trên khoảng nào sau đây?

A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
2. THÔNG HIỂU (10 CÂU)
Câu 1: Cho hàm số ![]() . Chọn khẳng định đúng trong các khẳng định sau:
. Chọn khẳng định đúng trong các khẳng định sau:
A. Hàm số nghịch biến trên khoảng ![]() .
.
B. Hàm số nghịch biến trên khoảng ![]() .
.
C. Hàm số nghịch biến trên khoảng ![]() .
.
D. Hàm số nghịch biến trên khoảng ![]()
Câu 2: Hàm số nào sau đây đồng biế trên ![]() ?
?
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Câu 3: Hàm số ![]() đồng biến trên khoảng nào?
đồng biến trên khoảng nào?
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() và
và ![]() .
.
Câu 4: Hàm số ![]() có bao nhiêu điểm cực trị?
có bao nhiêu điểm cực trị?
A. ![]()
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Câu 5: Cho hàm số ![]() có đạo hàm
có đạo hàm ![]() , với mọi
, với mọi ![]() . Hàm số đã cho đồng biến trên khoảng nào dưới đây?
. Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Câu 6: Hàm số ![]() có giá trị cực đại và giá trị cực tiểu lần lượt là
có giá trị cực đại và giá trị cực tiểu lần lượt là ![]() và
và ![]() . Khi đó
. Khi đó ![]() bằng:
bằng:
A. ![]()
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Câu 7: Cho hàm số ![]() có đạo hàm
có đạo hàm ![]() . Hàm số đã cho có bao nhiêu cực trị?
. Hàm số đã cho có bao nhiêu cực trị?
A. 2![]()
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Câu 8: Tìm giá trị cực tiểu của hàm số ![]() .
.
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Câu 9: Điểm cực tiểu của đồ thị hàm số ![]() là điểm:
là điểm:
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Câu 10: Cho hàm số ![]() . Mệnh đề nào sau đây đúng?
. Mệnh đề nào sau đây đúng?
A. Hàm số đồng biến trên khoảng ![]() .
.
B. Hàm số nghịch biến trên khoảng ![]() .
.
C. Hàm số đồng biến trên khoảng ![]() .
.
D. Hàm số đồng biến trên khoảng ![]() .
.
3. VẬN DỤNG (7 CÂU)
Câu 1: Cho hàm số ![]() có đạo hàm
có đạo hàm ![]() với mọi
với mọi ![]() . Hàm số
. Hàm số ![]() nghịch biến trên khoảng nào dưới đây?
nghịch biến trên khoảng nào dưới đây?
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Câu 2: Diện tích của tam giác có ba đỉnh là ba điểm cực trị của hàm số ![]() là:
là:
A. ![]()
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Câu 3: Tất cả các giá trị tham số ![]() để hàm số
để hàm số ![]() đồng biến trên
đồng biến trên ![]() là:
là:
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Câu 4: Cho hàm số ![]() . Hỏi hàm số
. Hỏi hàm số ![]() đồng biến trên khoảng nào dưới đây?
đồng biến trên khoảng nào dưới đây?
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Câu 5: Có bao nhiêu số nguyên ![]() để đồ thị hàm số
để đồ thị hàm số ![]() + 2024 có hai điểm cực trị nằm về 2 phía của trục tung?
+ 2024 có hai điểm cực trị nằm về 2 phía của trục tung?
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Câu 6: Tập hợp tất cả các giá trị thực của tham số ![]() để hàm số
để hàm số ![]() đồng biến trên từng khoảng xác định là:
đồng biến trên từng khoảng xác định là:
A. [![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Câu 7: Cho hàm số ![]() liên tục trên
liên tục trên ![]() và đồ thị có 3 điểm cực trị như hình dưới đây:
và đồ thị có 3 điểm cực trị như hình dưới đây:

Số điểm cực trị của hàm số ![]() là:
là:
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
4. VẬN DỤNG CAO (3 CÂU)
Câu 1: Cho hàm số ![]() , với
, với ![]() là tham số. Hỏi có bao nhiêu giá trị nguyên của
là tham số. Hỏi có bao nhiêu giá trị nguyên của ![]() thuộc đoạn
thuộc đoạn ![]() để hàm số đồng biến trên khoảng
để hàm số đồng biến trên khoảng ![]() ?
?
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Câu 2: Gọi ![]() là tập hợp các giá trị của tham số
là tập hợp các giá trị của tham số ![]() để hàm số
để hàm số ![]() có hai điểm cực trị
có hai điểm cực trị ![]() thỏa mãn
thỏa mãn ![]() . Tổng các phần tử của
. Tổng các phần tử của ![]() bằng:
bằng:
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Câu 3: Có bai nhiêu giá trị nguyên của tham số ![]() sao cho ứng với mỗi
sao cho ứng với mỗi ![]() , hàm số
, hàm số ![]() có đúng một điểm cực trị thuộc khoảng
có đúng một điểm cực trị thuộc khoảng ![]() ?
?
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
B. TRẮC NGHIỆM ĐÚNG SAI
Câu 1. Cho hàm số ![]() xác định, liên tục trên
xác định, liên tục trên ![]() và có đồ thị như hình vẽ dưới đây. Mệnh đề nào sau đây đúng?
và có đồ thị như hình vẽ dưới đây. Mệnh đề nào sau đây đúng?
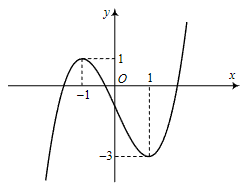
a) Hàm số đồng biến trên khoảng ![]() .
.
b) Điểm cực đại của đồ thị hàm số có tọa độ là ![]() .
.
c) Hàm số nghịch biến trên khoảng ![]() .
.
d) Phương trình đường thẳng đi qua hai điểm cực trị của hàm số là ![]() .
.
Đáp án:
a) Đ
b) S
c) Đ
d) S
Câu 2. Cho hàm số ![]() có
có ![]() .
.
a) Hàm số ![]() đồng biến trên khoảng
đồng biến trên khoảng ![]() và
và ![]() .
.
b) Hàm số ![]() nghịch biến trên khoảng
nghịch biến trên khoảng ![]() .
.
c) Hàm số đã cho không có cực trị.
d) Hàm số đã cho có 1 điểm cực đại.
Đáp án:
a) Đ
b) S
c) S
d) Đ
Câu 3. Cho hàm số ![]()
a) Điểm cực đại của hàm số là ![]() .
.
b) Giá trị cực tiểu của hàm số là ![]() .
.
c) Hàm số đã cho đồng biến trên khoảng ![]() .
.
d) Giả sử hàm số đã cho có hai điểm cực trị là ![]() và
và ![]() , khi đó giá trị
, khi đó giá trị ![]() .
.
Đáp án:
a) S
b) Đ
c) S
d) Đ
Câu 4. Cho hàm số ![]()
a) Đồ thị hàm số không có cực trị.
b) Độ dài khoảng cách giữa hai điểm cực trị là ![]() .
.
c) Hàm số đã cho đồng biến trên khoảng ![]() .
.
d) Hàm số đã cho nghịch biến trên khoảng ![]() .
.
Đáp án:
a) S
b) Đ
c) Đ
d) S

Đủ kho tài liệu môn học
=> Tài liệu sẽ được gửi ngay và luôn
Cách tải:
- Bước 1: Chuyển phí vào STK: 1214136868686 - cty Fidutech - MB
- Bước 2: Nhắn tin tới Zalo Fidutech - nhấn vào đây để thông báo và nhận tài liệu
=> Giáo án toán 12 chân trời sáng tạo
Từ khóa: câu hỏi trắc nghiệm toán 12 chân trời sáng tạo, đề trắc nghiệm toán 12 chân trời sáng tạo có đáp án, trắc nghiệm 12 toán chân trời sáng tạo trọn bộ, tổng hợp đề trắc nghiệm ôn tập toán 12 CTSTTài liệu giảng dạy môn Toán THPT
