HOẠT ĐỘNG CỦA GV- HS

DỰ KIẾN SẢN PHẨM

Bước 1: GV chuyển giao nhiệm vụ học tập.

- GV đặt câu hỏi và cùng HS nhắc lại kiến thức phần lí thuyết cần ghi nhớ trong bài “Tính đơn điệu của hàm số” trước khi thực hiện các phiếu bài tập.

Bước 2: Học sinh thực hiện nhiệm vụ học tập.

- HS tiếp nhận nhiệm vụ, ghi nhớ lại kiến thức, trả lời câu hỏi.

Bước 3: Báo cáo kết quả hoạt động, thảo luận.

- Đại diện một số HS đứng tại chỗ trình bày kết quả.

Bước 4: Đánh giá kết quả thực hiện nhiệm vụ học tập.

- GV đưa ra nhận xét, đánh giá chuẩn kiến thức.

1. Tính đơn điệu của hàm số

Cho hàm số  có đạo hàm trên .

Nếu  với mọi  thuộc  thì hàm số  đồng biến trên .

 Nếu  với mọi  thuộc  thì hàm số  nghịch biến trên .

Chú ý: Khi xét tinh đơn điệu của hàm số mà chưa cho khoảng , ta hiểu xét tính đơn điệu của hàm số đó trên tập xác định của nó.

Các bước thực hiện

Để xét tính đơn điệu của hàm số , ta thực hiện các bước sau:

Bước 1: Tìm tập xác định  của hàm số.

Bước 2: Tính đạo hàm  của hàm số. Tìm các điểm  thuộc  mà tại đó đạo hàm  bằng 0 hoặc đạo hàm không tồn tại.

Bước 3: Xét dấu  và lập bảng biến thiên.

Bước 4: Nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số.

Ví dụ: Tìm các khoảng đơn điệu của hàm số .

- Tập xác định:

- Ta có:

Bảng biến thiên:

Vậy hàm số đồng biến trên các khoảng  và ,  nghịch biến trên các khoảng  và .

Chú ý:

a) Nếu hàm số  có đạo hàm trên ,  với mọi  và  chỉ tại một số hữu hạn điểm thì hàm số đồng biến trên .

b) Nếu hàm số  có đạo hàm trên ,  với mọi  và  chỉ tại một số hữu hạn điểm thì hàm số nghịch biến trên .

c) Nếu  với mọi  thì hàm số không đổi trên .

Ví dụ: Các khoảng đơn điệu của hàm số

- Hàm số đã cho có tập xác định

- Ta có:  với ;

Bảng biến thiên của hàm số như sau:

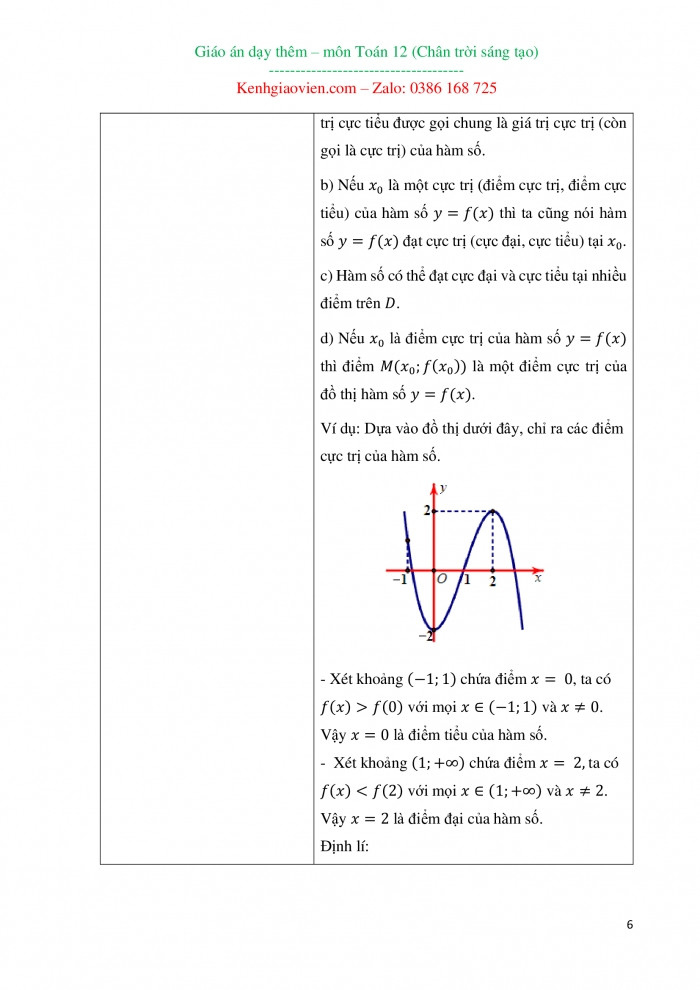
Vậy hàm số nghịch biến trên  và .

2. Cực trị của hàm số

Khái niệm

Cho hàm số  xác định trên tập hợp  và .

· Nếu tồn tại một khoảng  chứa điểm  và  sao cho  với mọi  thì  được gọi là một điểm cực đại,  được gọi là giá trị cực đại của hàm số , kí hiệu .

· Nếu tồn tại một khoảng  chứa điểm  và  sao cho  với mọi  thì  được gọi là một điểm cực tiểu,  được gọi là giá trị cực tiểu của hàm số , kí hiệu .

Chú ý:

a) Điểm cực đại và điểm cực tiểu được gọi chung là điểm cực trị của hàm số. Giá trị cực đại và giá trị cực tiểu được gọi chung là giá trị cực trị (còn gọi là cực trị) của hàm số.

b) Nếu  là một cực trị (điểm cực trị, điểm cực tiểu) của hàm số  thì ta cũng nói hàm số  đạt cực trị (cực đại, cực tiểu) tại .

c) Hàm số có thể đạt cực đại và cực tiểu tại nhiều điểm trên .

d) Nếu  là điểm cực trị của hàm số  thì điểm  là một điểm cực trị của đồ thị hàm số .

Ví dụ: Dựa vào đồ thị dưới đây, chỉ ra các điểm cực trị của hàm số.

- Xét khoảng  chứa điểm , ta có  với mọi  và .

Vậy  là điểm tiểu của hàm số.

-  Xét khoảng  chứa điểm ta có  với mọi  và .

Vậy  là điểm đại của hàm số.

Định lí:

Gải sử hàm số  liên tục trên khoảng  chứa điểm  và có đoạ hàm trên các khoảng  và . Khi đó:

a) Nếu  với mọi  và  với mọi  thì hàm số  đạt cực tiểu tại điểm

b)  Nếu  với mọi  và  với mọi  thì hàm số  đạt cực đại tại điểm

Nhận xét: Để tìm cực trị của hàm số ta thực hiện các bước sau:

Bước 1: Tìm tập xác định  của hàm số.

Bước 2: Tính đạo hàm  của hàm số. Tìm các điểm  thuộc  mà tại đó đạo hàm  bằng 0 hoặc đạo hàm không tồn tại.

Bước 3: Lập bảng biến thiên của hàm số.

Bước 4: Từ bảng biến thiên kết luận về cực trị của hàm số.

Ví dụ: Tìm điểm cực trị của hàm số

- Tập xác định: .

- Ta có:

 hoặc .

Bảng biến thiên:

Vậy hàm số đạt cực đại tại  và đạt cực tiểu tại .

Chú ý:

a) Nếu  và  không đổi dấu khi  qua điểm thì hàm số không có cực trị tại .

b) Nếu  không đổi dấu trên khoảng  thì  không có cực trị trên khoảng đó.

PHIẾU BÀI TẬP SỐ 1

DẠNG 1: Xét tính đơn điệu của hàm số cho bởi biểu thức

Phương pháp giải:

Để xét tính đơn điệu của hàm số , ta thực hiện các bước sau:

Bước 1: Tìm tập xác định  của hàm số.

Bước 2: Tính đạo hàm  của hàm số. Tìm các điểm  thuộc  mà tại đó đạo hàm  bằng 0 hoặc đạo hàm không tồn tại.

Bước 3: Xét dấu  và lập bảng biến thiên.

Bước 4: Nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số.

Bài 1. Tìm các khoảng đơn điệu của các hàm số sau:

Bài 2: Tìm các khoảng đơn điệu của hàm số:

Bài 3: Tìm các khoảng đơn điệu của hàm số  trên

Bài 4: Tìm các khoảng đồng biến và nghịch biến của hàm số

Bài 5: Tìm các khoảng đồng biến và nghịch biến của hàm số:

Bài 6: Tìm khoảng đồng biến của các hàm số sau:

DẠNG 1:

Bài 1:

a. .

- Tập xác định:

- Ta có:

               hoặc

 Bảng biến thiên:

Vậy hàm số đồng biến trên khoảng  và ; hàm số nghịch biến trên khoảng .

b. .

- Tập xác định:

- Ta có: .

Vậy hàm số đồng biến trên khoảng .

c. .                  

- Tập xác định:

- Ta có: . 

                hoặc

 Bảng biến thiên:

Vậy hàm số đồng biến trên khoảng  và ; hàm số nghịch biến trên khoảng .

d. .                  

- Tập xác định:

- Ta có:

               hoặc .

Bảng biến thiên:

Vậy hàm số đồng biến trên khoảng  và ; hàm số nghịch biến trên khoảng  và .

Bài 2:

a. .          

- Tập xác định:

- Ta có:  với ;

Bảng biến thiên của hàm số như sau:

Vậy hàm số đồng biến trên  và .

b. .

- Tập xác định:

- Ta có:  với ;

Vậy hàm số nghịch biến trên  và .

c. .                  

- Tập xác định:

Ta có:

Bảng biến thiên:

d. .                  

- Tập xác định:

- Ta có:  với mọi .

Vậy hàm số nghịch biến trên các khoảng  và .

Bài 3:

Trên khoảng  thì .

Ta có: .

Vậy hàm số đồng biến trên khoảng .

Bài 4:

- Tập xác định: .

Suy ra: .

Bảng xét dấu của :

Từ bảng xét dấu ta có hàm số đồng biến trên các khoảng  và , nghịch biến trên các khoảng  và .

Bài 5:

a) .          

- Tập xác định: .

Ta có:

Khi đó: .

Bảng xét dấu của :

Vậy hàm số đồng biến trên các khoảng  và , nghịch biến trên các khoảng  và .

b. .

- Tập xác định: .

Ta có:

Khi đó:

Bảng biến thiên:

Vậy hàm số đồng biến trên khoảng  và nghịch biến trên khoảng

Bài 6:

a.  

- Tập xác định: .

- Ta có: .

Vậy hàm số đồng biến trên .

b. .

- Tập xác định: .

- Ta có: .

Vậy hàm số đồng biến trên .

PHIẾU BÀI TẬP SỐ 2

DẠNG 2: Xét tính đơn điệu của hàm hợp cho bởi bảng biến thiên hoặc đồ thị của hàm số  hoặc . 

Phương pháp giải:

Nếu  với mọi  thuộc  thì hàm số  đồng biến trên .

 Nếu  với mọi  thuộc  thì hàm số  nghịch biến trên .

Bài 1: Cho hàm số  có đồ thị như hình vẽ sau:

Tìm khoảng đơn điệu của hàm số .

Bài 2: Cho hàm số  có bảng biến thiên như sau:

Hàm số đã cho đồng biến, nghịch biến trên khoảng nào?

Bài 3: Cho hàm số  xác định, liên tục trên  và có bảng biến thiên:

Tìm các khoảng đồng biến của hàm số .

Bài 4: Cho hàm số  có bảng biến thiên:

Hàm số  nghịch biến trên các khoảng nào?

Bài 5: Cho hàm số  có đạo hàm liêm tục trên . Hàm số  có đồ thị như hình vẽ sau:

Tìm các khoảng đơn điệu của hàm số .

DẠNG 2:

Bài 1:

Kết luận: Hàm số đồng biến trên các khoảng  và , hàm số nghịch biến trên khoảng .

Bài 2:

Kết luận: Hàm số đồng biến trên các khoảng  và , hàm số nghịch biến trên khoảng .

Bài 3:

Đặt

Ta có:

- Bảng biến thiên:

Vậy hàm số  đồng biến trên các khoảng  và .

Bài 4:

- Đặt .

Ta có: .

- Bảng biến thiên:

Vậy hàm số  nghịch biến trên các khoảng  và .

Bài 5:

Ta có: .

Dựa vào đồ thị  ta có:

Vậy hàm số  đồng biến trên các khoảng  và , nghịch biến trên các khoảng  và .

PHIẾU BÀI TẬP SỐ 3

DẠNG 3: Tìm điều kiện của tham số để hàm số đồng biến, nghịch biến trên một khoảng.

* Hàm số đồng biến, nghịch biến trên một khoảng cho trước.

Phương pháp giải:

- Kiểm tra tập xác định của hàm số.

- Tính  và tìm điều kiện của tham số để  hoặc  trên khoảng .

* Hàm số đồng biến, nghịc biến trên tập xác định.

Phương pháp giải:

- Đối với hàm đa thức bậc ba:

Tính , khi đó:

· Hàm số  đồng biến trên ℝ  và .

· Hàm số  nghịch biến trên ℝ  và .

- Đối với hàm phân thức bậc nhất:

Tính  khi đó:

· Hàm số đồng biến trên các khoảng xác định khi  hay .

· Hàm số đồng biến trên các khoảng xác định khi  hay .

Bài 1: Tìm các giá trị của tham số  để hàm số đồng biến trên .

Bài 2: Tìm các giá trị của tham số  để hàm số  nghịch biến trên .

Bài 3: Tìm  để hàm số  luôn nghịch biến trên từng khoảng xác định.

Bài 4: Cho hàm số , tìm tất cả các giá trị của tham số  để hàm số nghịch biến trên khoảng .

Bài 5: Có bao nhiêu giá trị  nguyên để hàm số đồng biến trên khoảng

Bài 6: Tìm  để hàm số  nghịch biến trên khoảng

DẠNG 3:

Bài 1:

a.

- Tập xác định: .

- Ta có:

Hàm số đồng biến trên .

Vậy  thì hàm số luôn đồng biến trên .

b.

- Tập xác định: .

- Với  hàm số trở thành: . Suy ra hàm số đồng biến trên khoảng .

Vậy  không thỏa mãn.

- Với , ta có: .

Hàm số đồng biến trên  

  (thỏa mãn).

Vậy .

Bài 2:

- Tập xác định: .

- Với , hàm số trở thành .

Có: Suy ra hàm số nghịch biến trên , chọn  thỏa mãn.

- Với , ta có: .

Hàm số nghịch biến trên  

Vậy  thì hàm số đã cho nghịch biến trên .

Bài 3: 

- Tập xác định: .

Hàm số nghịch biến trên từng khoảng xác định  trên

.

Vậy thì hàm số đã cho nghịch biến trên từng khoảng xác định của nó.

Bài 4:

- Tập xác định: .

Ta có:

Đặt

Có:

- Bảng biến thiên:

Khi đó: với  .

Vậy  thì hàm số đã cho nghịch biến trên khoảng .

Bài 5:

- Tập xác định: .

Hàm số đã cho đồng biến trên khoảng  khi và chỉ khi .

.

Đặt

Khi đó:

- Bảng biến thiên:

Từ bảng biến thiên ta có: .

Vì  suy ra .

Bài 6:

Đặt . Ta có hàm số  nghịch biến trên .

Khi thì .

Xét hàm  trên khoảng . Ta có: .

Hàm đã cho nghịch biến trên khoảng  hàm số  đồng biến trên khoảng  .

Vậy .

PHIẾU BÀI TẬP SỐ 4.

DẠNG 4: Tìm cực trị của hàm số

Phương pháp giải:

Để tìm cực trị của hàm số ta thực hiện các bước sau:

Bước 1: Tìm tập xác định  của hàm số.

Bước 2: Tính đạo hàm  của hàm số. Tìm các điểm  thuộc  mà tại đó đạo hàm  bằng 0 hoặc đạo hàm không tồn tại.

Bước 3: Lập bảng biến thiên của hàm số.

Bước 4: Từ bảng biến thiên kết luận về cực trị của hàm số.

Bài 1: Cho hàm số . Xác định các điểm cực trị của hàm số.

Bài 2: Hàm số  có bao nhiêu cực trị?

Bài 3: Gọi  là các điểm cực trị của đồ thị hàm số . Tính khoảng cách .

Bài 4: Cho hàm số . Tìm các điểm cực trị của hàm số trên.

Bài 5: Hàm số  có bao nhiêu cực trị?

Bài 6: Cho hàm số  có bảng biến thiên như sau:

Tìm số điểm cực trị của hàm số