Giáo án điện tử chuyên đề Toán 12 chân trời Bài 2: Phân bố Bernoulli và phân bố nhị thức

CHÀO MỪNG CẢ LỚP ĐẾN VỚI TIẾT HỌC HÔM NAY!

KHỞI ĐỘNG

Một loại hạt giống có xác suất nảy mầm là 0,9. Bác Hoan gieo 100 hạt giống đó một cách độc lập với nhau. Có người cho rằng “Trong 100 hạt giống bác Hoan gieo sẽ có đúng 90 hạt nảy mầm”.

Nhận định đó là đúng hay sai?

CHUYÊN ĐỀ III: BIẾN NGẪU NHIÊN RỜI RẠC. CÁC SỐ ĐẶC TRƯNG CỦA BIẾN NGẪU NHIÊN RỜI RẠC

BÀI 2: PHÂN BỐ BERNOULLI VÀ PHÂN BỐ NHỊ THỨC

1

NỘI DUNG BÀI HỌC

Phân bố Bernoulli

Phép thử lặp và công thức Bernoulli

Phân bố nhị thức

Phân bố Bernoulli

• HĐKP 1. Thuyền trưởng Vinh gửi một tín hiệu từ thuyền đến trạm điều khiển. Xác suất để trạm điều khiển thu được tín hiệu vô tuyến là 0,8. Gọi là số tín hiệu vô tuyến của thuyền trưởng Vinh được thu bởi trạm điều khiển. Hãy tính kì vọng và phương sai của .

Khi trạm điều khiển thu được tín hiệu vô tuyến thì số tín hiệu vô tuyến của thuyền trưởng Vinh được thu bởi trạm điều khiển là 1.

Khi trạm điều khiển không thu được tín hiệu vô tuyến thì số tín hiệu vô tuyến của thuyền trưởng Vinh được thu bởi trạm điều khiển là 0.

Biến ngẫu nhiên rời rạc chỉ nhận hai giá trị là 0 và 1.

Giải:

• HĐKP 1. Thuyền trưởng Vinh gửi một tín hiệu từ thuyền đến trạm điều khiển. Xác suất để trạm điều khiển thu được tín hiệu vô tuyến là 0,8. Gọi là số tín hiệu vô tuyến của thuyền trưởng Vinh được thu bởi trạm điều khiển. Hãy tính kì vọng và phương sai của .

Giải:

Ta có bảng phân bố xác suất của

Khái niệm

Biến ngẫu nhiên rời rạc được gọi là có phân bố Bernoulli với tham số , kí hiệu là , nếu chỉ nhận hai giá trị là và , và .

Chú ý: Nếu thì và .

Ví dụ 1: Trong các biến ngẫu nhiên rời rạc sau, biến ngẫu nhiên rời rạc nào có phân bố Bernoulli? Xác định giá trị của tham số và tính phương sai của các biến ngẫu nhiên rời rạc có phân bố Bernoulli đó.

a) là số mặt sấp xuất hiện khi gieo một đồng xu cân đối và đồng chất.

b) là số mặt sấp xuất hiện khi gieo hai đồng xu cân đối và đồng chất.

c) Gieo hai con xúc xắc cân đối và đồng chất. Biến ngẫu nhiên rời rạc nhận giá trị bằng 1 nếu hai mặt có cùng số chấm xuất hiện, bằng 0 nếu ngược lại.

Giải:

b) nhận ba giá trị là và nên không có phân bố Bernoulli.

c)nhận hai giá trị là và .

Vì cókết quả thuận lợi cho biến cố “” trong tổng số 36 kết quả có thể xảy ra nên

Giải:

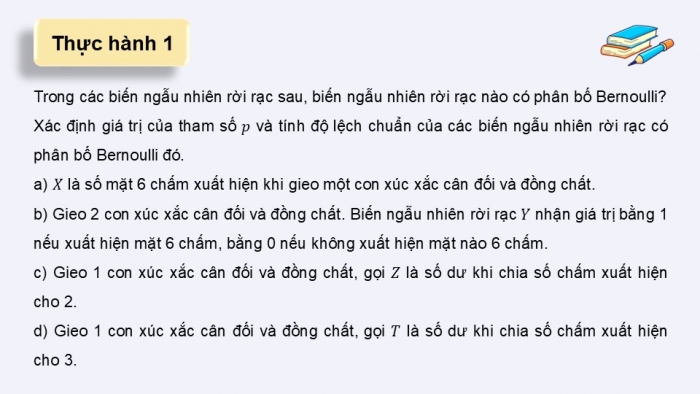
Thực hành 1

Trong các biến ngẫu nhiên rời rạc sau, biến ngẫu nhiên rời rạc nào có phân bố Bernoulli?

Xác định giá trị của tham số và tính độ lệch chuẩn của các biến ngẫu nhiên rời rạc có phân bố Bernoulli đó.

a) là số mặt 6 chấm xuất hiện khi gieo một con xúc xắc cân đối và đồng chất.

b) Gieo 2 con xúc xắc cân đối và đồng chất. Biến ngẫu nhiên rời rạc nhận giá trị bằng 1 nếu xuất hiện mặt 6 chấm, bằng 0 nếu không xuất hiện mặt nào 6 chấm.

c) Gieo 1 con xúc xắc cân đối và đồng chất, gọi là số dư khi chia số chấm xuất hiện cho 2.

d) Gieo 1 con xúc xắc cân đối và đồng chất, gọi là số dư khi chia số chấm xuất hiện cho 3.

a) chỉ nhận hai giá trị là 0 và 1.

Chỉ có 1 kết quả thuận lợi cho biến cố “” trong tổng

Giải:

b) nhận hai giá trị là 0 và 1.

Vì có 7 kết quả thuận lợi cho biến cố trong tổng số 36 kết quả xảy ra nên

Giải:

c) nhận hai giá trị là 0 và 1.

d) nhận ba giá trị là 0; 1 và 2 nên không có phân bố Bernoulli.

Phép thử lặp và công thức Bernoulli

Giải:

• HĐKP 2. Xét phép thử ngẫu nhiên là “Gieo một đồng xu cân đối và đồng chất”. Hãy liệt kê tất cả các kết quả có thể xảy ra khi thực hiện phép thử ba lần liên tiếp một cách độc lập.

Kí hiệu là kết quả đồng xu xuất hiện mặt sấp và là kết quả đồng xu xuất hiện mặt ngửa.

Khi thực hiện phép thử ba lần liên tiếp, các kết quả có thể xảy ra là: , .

Kết luận

Giả sử là một phép thử ngẫu nhiên. Hoạt động lặp lại nhiều lần phép thử được gọi là phép thử lặp nếu các lần thực hiện phép thử một cách độc lập với nhau, tức là kết quả của mỗi lần thực hiện phép thử không ảnh hưởng đến kết quả của các lần thử khác. Số lần thực hiện phép thử được gọi là số lần lặp của phép thử lặp đó.

Ví dụ 2: Trong các hoạt động sau, hoạt động nào là phép thử lặp? Hãy cho biết số lần lặp của các hoạt động là phép thử lặp.

a) Gieo một con xúc xắc cân đối và đồng chất 10 lần một cách độc lập.

b) Một hộp chứa 4 viên bi xanh và 3 viên bi trắng có cùng kích thước và khối lượng. Lấy ra ngẫu nhiên 1 viên bi từ hộp, xem màu rồi trả lại hộp. Thực hiện hoạt động này 5 lần.

c) Một hộp chứa 4 viên bi xanh và 3 viên bi trắng có cùng kích thước và khối lượng. Lấy ra ngẫu nhiên 1 viên bi từ hộp, xem màu và bỏ ra ngoài hộp. Thực hiện hoạt động này 2 lần.

Giải:

a) Gọi là phép thử “Gieo một con xúc xắc cân đối và đồng chất”.

Trong hoạt động ở câu a), phép thử được lặp lại 10 lần một cách độc lập.

Do đó hoạt động này là phép thử lặp với số lần lặp là 10.

b) Gọi là phép thử “Lấy ra ngẫu nhiên 1 viên bi từ một hộp chứa 4 viên bi xanh và 3 viên bi đỏ có cùng kích thước và khối lượng”.

Trong hoạt động ở câu b), phép thử được lặp lại 5 lần và sau mỗi lần thử, viên bi được trả lại hộp nên không làm ảnh hưởng đến kết quả của các lần thử khác, tức là 5 lần thử được thực hiện độc lập.

Vậy hoạt động ở câu b) là phép thử lặp với số lần lặp là 5.

Giải:

c) Xét hoạt động ở câu c).

Nếu lần thử thứ nhất lấy được viên bi màu xanh thì xác suất lấy được viên bi màu

Ngược lại, nếu lần thử thứ nhất lấy được viên bi màu trắng thì xác suất lấy được

Do đó kết quả của lần thử thứ nhất ảnh hưởng đến kết quả của lần thử thứ hai.

Vậy hoạt động c) không phải là phép thử lặp.

Kết luận

Cho phép thử và là một biến cố liên quan đến phép thử . Giả sử xác suất biến cố xảy ra ở mỗi lần thực hiện phép thử là với .

Thực hiện lặp lại lần phép thử một cách độc lập. Kí hiệu là biến cố “Biến cố xảy ra đúng lần trong lần thực hiện phép thử ”, Khi đó xác suất của được xác định bởi công thức Bernoulli sau:

Ví dụ 3: Trong không gian, vệ tinh Alpha truyền lần lượt từng tín hiệu đến vệ tinh Beta. Biết rằng mỗi lần vệ tinh Alpha truyền tín hiệu, xác suất vệ tinh Beta nhận được thành công tín hiệu đó đều bằng 0,95. Giả sử vệ tinh Alpha truyền 10 tín hiệu đến vệ tinh Beta một cách độc lập. Tính xác suất của các biến cố sau:

: “Vệ tinh Beta nhận được thành công 8 tín hiệu”;

: “Vệ tinh Beta nhận được thành công ít nhất 9 tín hiệu”.

(Làm tròn kết quả đến hàng phần trăm.)

Giải:

Gọi là phép thử “Vệ tinh Alpha truyền 1 tín hiệu đến vệ tinh Beta”.

Theo đề bài, phép thử được lặp 10 lần một cách độc lập.

Gọi là biến cố “Vệ tinh Beta nhận thành công tín hiệu từ vệ tinh Alpha”.

Ta có

Gọi là biến cố “Vệ tinh Beta nhận thành công tín hiệu trong 10 tín hiệu”, với Áp dụng công thức Bernoulli, ta có

với

Do đó

Vì với nên

Trong tình huống mở đầu (trang 64), hãy tính xác suất của biến cố “Trong 100 hạt giống bác Hoan gieo, có đúng 90 hạt nảy mầm”.

Thực hành 2

Giải:

Gọi là phép thử “Gieo ngẫu nhiên một hạt giống”. Theo đề bài, phép thử được lặp lại 100 lần một cách độc lập.

Gọi là biến cố “Hạt giống nảy mầm”. Ta có

Gọi là biến cố “Có hạt giống nảy mầm trong 100 hạt giống được gieo”, với .

Áp dụng công thức Bernoulli, ta có: , với

Gọi là biến cố “Trong 100 hạt giống bác Hoan gieo, có đúng 90 hạt nảy mầm”.

Thực hành 3

Tỉ lệ người lao động có bằng đại học ở một khu công nghiệp là 30%. Tiến hành phỏng vấn lần lượt 10 người lao động được lựa chọn ngẫu nhiên một cách độc lập từ khu công nghiệp đó. Tính xác suất của các biến cố sau:

: “Có đúng 3 trong 10 người được phỏng vấn có bằng đại học”;

: “Có ít nhất 1 trong 10 người được phỏng vấn có bằng đại học”.

Giải:

Gọi là phép thử “Phỏng vấn ngẫu nhiên một người lao động từ khi công nghiệp”. Theo đề bài, phép thử được lặp lại 10 lần một cách độc lập.

Gọi là biến cố “Người lao động có bằng đại học”. Ta có

Gọi là biến cố “Có người có bằng đại học trong 10 người lao động được phỏng vấn”, với .

Thực hành 3

Tỉ lệ người lao động có bằng đại học ở một khu công nghiệp là 30%. Tiến hành phỏng vấn lần lượt 10 người lao động được lựa chọn ngẫu nhiên một cách độc lập từ khu công nghiệp đó. Tính xác suất của các biến cố sau:

: “Có đúng 3 trong 10 người được phỏng vấn có bằng đại học”;

: “Có ít nhất 1 trong 10 người được phỏng vấn có bằng đại học”.

Giải:

Áp dụng công thức Bernoulli, ta có:

, với .

Do đó,

Phân bố nhị thức

Giải:

• HĐKP 3. Một công ty được nhận thấy xác suất một bệnh nhân có phản ứng phụ khi được điều trị bằng một loại thuốc M là 0,08. Chọn ngẫu nhiên 10 000 bệnh nhân được điều trị một cách độc lập bằng thuốc M. Gọi là số bệnh nhân có phản ứng phụ trong 10 000 bệnh nhân đó. Hãy viết biểu thức tính kì vọng của .

Gọi là phép thử “Chọn ngẫu nhiên một bệnh nhân”. Theo đề bài, phép thử được lặp lại 10 000 lần một cách độc lập.

Gọi là biến cố “Bệnh nhân có phản ứng phụ với thuốc M”. Ta có

Gọi là biến cố “Có bệnh nhân có phản ứng phụ trong 10 000 bệnh nhân đó”, với .

Giải:

• HĐKP 3. Một công ty được nhận thấy xác suất một bệnh nhân có phản ứng phụ khi được điều trị bằng một loại thuốc M là 0,08. Chọn ngẫu nhiên 10 000 bệnh nhân được điều trị một cách độc lập bằng thuốc M. Gọi là số bệnh nhân có phản ứng phụ trong 10 000 bệnh nhân đó. Hãy viết biểu thức tính kì vọng của .

Áp dụng công thức Bernoulli, ta có:

với .

Biểu thức tính kì vọng là:

Định nghĩa

Cho số nguyên dương và số thực . Biến ngẫu nhiên rời rạc được gọi là có phân bố nhị thức nếu chỉ nhận các giá trị thuộc tập hợp và

, với .

Chú ý:

• Cho phép thử và biến cố liên quan đến phép thử với xác suất Thực hiện phép thử lặp lại lần một cách độc lập và gọi là số lần xảy ra biến cố . Khi đó là biến ngẫu nhiên rời rạc có phân bố nhị thức
• Khi thì phân bố nhị thức là phân bố Bernoulli.

Ví dụ 4: Trong các biến ngẫu nhiên rời rạc sau, biến ngẫu nhiên rời rạc nào có phân bố nhị thức?

a) Một hộp chứa 4 viên bi xanh và 1 viên bi đỏ, các viên bi cùng kích thước và khối lượng. Lấy ra ngẫu nhiên đồng thời 2 viên bi từ hộp. Gọi là số bi đỏ được lấy ra trong 2 viên bi đó.

b) là số lần xuất hiện mặt 1 chấm khi gieo một con xúc xắc cân đối và đồng chất 4 lần liên tiếp một cách độc lập với nhau.

phân bố nhị thức

Giải:

Giải:

b) Gọi là phép thử “Gieo một con xúc xắc cân đối và đồng chất” và là biến cố “Xuất hiện mặt 1 chấm”.

là số lần xảy ra biến cố khi lặp 4 lần phép thử

Do phép thử được lặp 4 lần độc lập với nhau và xác suất xảy ra biến cố

Ví dụ 5: Trong một phân xưởng, tỉ lệ sản phẩm bị lỗi của một dây chuyền sản xuất là 0,2%. Nhân viên quản lí chất lượng chọn ngẫu nhiên một cách độc lập sản phẩm của dây chuyền sản xuất để kiểm tra.

a) Tính xác suất để nhân viên quản lí chất lượng tìm ra ít nhất một sản phẩm bị lỗi khi

b) Tìm giá trị nhỏ nhất của sao cho xác suất tìm ra ít nhất một sản phẩm bị lỗi lớn hơn . (Làm tròn kết quả đến hàng phần nghìn.)

Giải:

Gọi là phép thử “Chọn ngẫu nhiên 1 sản phẩm của dây chuyền”, là biến cố “Sản phẩm lấy ra bị lỗi” và là số lần xảy ra biến cố khi lặp lần phép thử .

Do phép thử được thực hiện lần độc lập với nhau và xác suất xảy ra biến cố trong mỗi lần thử đều bằng nên là biến ngẫu nhiên rời rạc có phân bố nhị thức

a) Khi thì xác suất tìm ra ít nhất một sản phẩm lỗi là

b) Xác suất tìm ra ít nhất một sản phẩm lỗi trong sản phẩm được kiểm tra là

là

Giải:

Ví dụ 6: Trong một phép lai, xác suất một cá thể tạo ra ở thế hệ mang biến dị tổ hợp

Gọi là số cá thể mang biến dị tổ hợp trong 3 cá thể được lựa chọn ngẫu nhiên một cách độc lập.

a) Lập bảng phân bố xác suất của . b) Tính kì vọng và phương sai của .

Giải:

a) Gọi là phép thử “Chọn ngẫu nhiên 1 cá thể ở thế hệ ” và là biến cố “Cá thể được chọn mang biến dị tổ hợp”.

Gọi là số lần xảy ra biến cố khi lặp 3 lần phép thử

Giải:

Do phép thử được thực hiện 3 lần một cách độc lập với nhau và xác suất xảy ra

Lần lượt tính với từ công thức trên, ta thu được bảng phân bố xác suất của như sau:

--------------------------------------

--------------------- Còn tiếp ----------------------