Giáo án điện tử toán 10 kết nối bài 4: Hệ bất phương trình bậc nhất hai ẩn (3 tiết)

NHIỆT LIỆT CHÀO MỪNG CẢ LỚP ĐẾN VỚI BÀI HỌC MỚI!

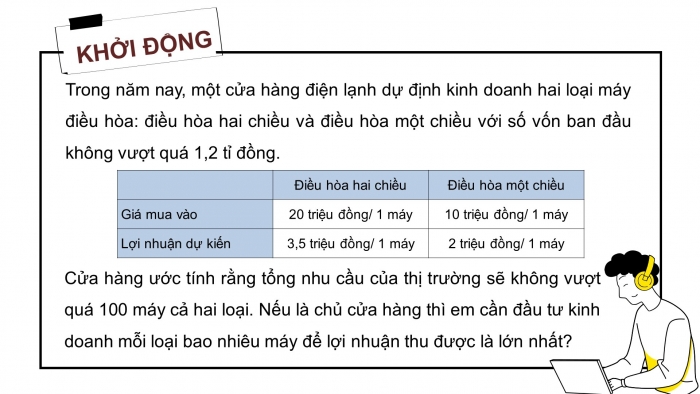
Trong năm nay, một cửa hàng điện lạnh dự định kinh doanh hai loại máy điều hòa: điều hòa hai chiều và điều hòa một chiều với số vốn ban đầu không vượt quá 1,2 tỉ đồng.

Cửa hàng ước tính rằng tổng nhu cầu của thị trường sẽ không vượt quá 100 máy cả hai loại. Nếu là chủ cửa hàng thì em cần đầu tư kinh doanh mỗi loại bao nhiêu máy để lợi nhuận thu được là lớn nhất?

BÀI 4

HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN (3 Tiết)

NỘI DUNG BÀI HỌC

Hệ bất phương trình bậc nhất hai ẩn

Biểu diễn miền nghiệm của hệ bất phương trình bậc nhất hai ẩn trên mặt phẳng tọa độ

Ứng dụng của hệ bất phương trình bậc nhất hai ẩn

TIẾT 1

1. Hệ bất phương trình bậc nhất hai ẩn

              Trong tình huống mở đầu, gọi x và y lần lượt là số máy điều hòa loại hai chiều và một chiều mà cửa hàng cần nhập. Tính số tiền vốn mà cửa hàng phải bỏ ra để nhập hai loại máy điều hòa theo x và y.

1. a) Do nhu cầu của thị trường không quá 100 máy nên x và y cần thỏa mãn điều kiện gì?
2. b) Vì số vốn mà chủ cửa hàng có thể đầu tư không vượt quá 1,2 tỉ đồng nên x và y phải thỏa mãn điều kiện gì?
3. c) Tính số tiền lãi mà cửa hàng dự kiến thu được theo x và y.

Giải

Số tiền vốn mà cửa hàng phải bỏ ra để mua hai loại máy điều hòa là:  20x + 10y (triệu đồng).

1. a) x + y ≤ 100
2. b) 20x + 10y ≤ 1 200
3. c) 3,5x + 2y.

Một hệ các bất phương trình trong HĐ1 được gọi là hệ bất phương trình bậc nhất hai ẩn.

Định nghĩa

• Hệ bất phương trình bậc nhất hai ẩn là một hệ gồm hai hay nhiều bất phương trình bậc nhất hai ẩn.
• Cặp số (x_o; y_o⁡) là nghiệm của một hệ bất phương trình bậc nhất hai ẩn khi (x_o; y_o⁡) đồng thời là nghiệm của tất cả các bất phương trình trong hệ đó.

Ví dụ 1:

Cho hệ bất phương trình:

1. a) Hệ trên có phải là hệ phương trình bậc nhất hai ẩn không?
2. b) Kiểm tra xem cặp số (x; y) = (0; 0) có phải là một nghiệm của hệ bất phương trình trên không?

Giải

1. a) Hệ bất phương trình đã cho là một hệ bất phương trình bậc nhất hai ẩn x và y.
2. b) Cặp số (x; y) = (0; 0) thỏa mãn cả ba bất phương trình của hệ nên nó là một nghiệm của hệ bất phương trình bậc nhất hai ẩn đã cho.

Luyện tập 1:

Trong tình huống mở đầu, gọi x và y lần lượt là số máy điều hòa loại hai chiều và một chiều mà cửa hàng cần nhập. Từ HĐ1, viết hệ phương trình hai ẩn x, y và chỉ ra một nghiệm của hệ này.

Giải

Ta có hệ bất phương trình:

Một nghiệm của hệ trên là:

(x; y) = (30; 20).

2. Biểu diễn miền nghiệm của hệ bất phương trình bậc nhất hai ẩn trên mặt phẳng tọa độ

HĐ2

Cho đường thẳng d: x + y = 150 trên mặt phẳng tọa độ Oxy. Đường thẳng này cắt hai trục tọa độ Ox và Oy tại hai điểm A và B.

150. a) Xác định các miền nghiệm D₁ ,D₂ , D₃ của bất phương trình tương ứng x ≥ 0; y ≥ 0 và x + y ≤
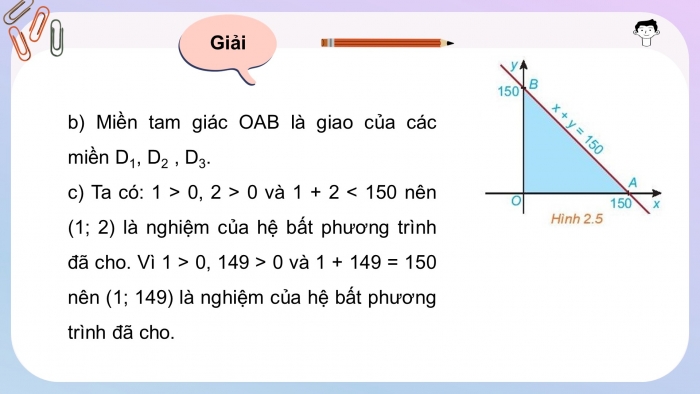
151. b) Miền tam giác OAB có phải là giao của các miền D₁, D₂, D₃ hay không?
152. c) Lấy một điểm trong tam giác OAB và kiểm tra xem tọa độ của các điểm đó có phải là nghiệm của hệ bất phương trình sau hay không:

Giải

1. a)

• Trục Oy có phương trình x = 0.

Điểm (1; 0) thỏa mãn 1 > 0, nên miền nghiệm D₁ của bất phương trình x ≥ 0 là nửa mặt phẳng bờ Oy chứa điểm (1; 0) (tính cả bờ Oy).

Trục Oy có phương trình y = 0.

Điểm (0; 1) ) thỏa mãn 1 > 0, nên miền nghiệm D₂ của bất phương trình y ≥ 0 là nửa mặt phẳng bờ Ox chứa điểm (0; 1) (tính cả bờ Ox).

Vẽ đường thẳng d: x + y = 150. Tọa độ điểm O(0; 0) thỏa mãn 0 + 0 < 150.

Miền nghiệm D3 của bất phương trình x + y ≤ 150 là nửa mặt phẳng bờ d chứa gốc tọa độ (tính cả bờ d).

3. b) Miền tam giác OAB là giao của các miền D₁, D₂ , D₃.
4. c) Ta có: 1 > 0, 2 > 0 và 1 + 2 < 150 nên (1; 2) là nghiệm của hệ bất phương trình đã cho. Vì 1 > 0, 149 > 0 và 1 + 149 = 150 nên (1; 149) là nghiệm của hệ bất phương trình đã cho.

Định nghĩa

• Trong mặt phẳng tọa độ, tập hợp các điểm có tọa độ là nghiệm của hệ bất phương trình bậc nhất hai ẩn là miền nghiệm của hệ bất phương trình đó.
• Miền nghiệm của hệ là giao các miền nghiệm của các bất phương trình trong hệ.

Ví dụ 2:

Biểu diễn miền nghiệm của hệ bất phương trình sau trên mặt phẳng tọa độ:

Giải

Bước 1: Xác định miền nghiệm D₁ của bất phương trình 7x + 4y  2 400 và gạch bỏ miền còn lại.

• Vẽ đường thẳng d: 7x + 4y = 2 400
• Vì 7. 0 + 4. 0 = 0 < 2 400 nên tọa độ O (0; 0) thỏa mãn bất phương trình 7x + 4y 2 400.

Do đó, miền nghiệm D₁ của bất phương trình 7x + 4y  2 400 là nửa mặt phẳng bờ d chứa gốc tọa độ O.

Bước 2: Tương tự, miền nghiệm D₂ của bất phương trình x + y ≤ 100 là nửa mặt phẳng bờ d’ chứa gốc tọa độ O.

Bước 3: Tương tự, miền nghiệm D₃ của bất phương trình x ≥ 0 là nửa mặt phẳng bờ Oy chứa điểm (1; 0).

Khi đó, miền không bị gạch chính là miền nghiệm của các bất phương trình trong hệ. Vậy miền  nghiệm của hệ là miền không bị gạch.

Cách xác định miền nghiệm của hệ bất phương trình bậc nhất hai ẩn:

• Trên cùng một mặt phẳng tọa độ, xác định miền nghiệm của mỗi bất phương trình bậc nhất hai ẩn trong hệ và gạch bỏ miền còn lại.
• Miền không bị gạch là miền nghiệm của hệ bất phương trình đã cho.