Giáo án điện tử toán 10 kết nối bài 14: Các số đặc trưng đo độ phân tán

CHÀO MỪNG CÁC EM ĐẾN VỚI TIẾT HỌC HÔM NAY!

KHỞI ĐỘNG

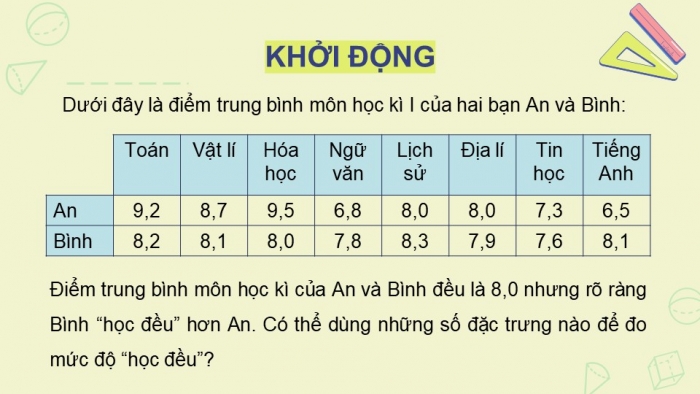
Dưới đây là điểm trung bình môn học kì I của hai bạn An và Bình:

Điểm trung bình môn học kì của An và Bình đều là 8,0 nhưng rõ ràng Bình “học đều” hơn An. Có thể dùng những số đặc trưng nào để đo mức độ “học đều”?

BÀI 14: CÁC SỐ ĐẶC TRƯNG ĐO ĐỘ PHÂN TÁN (2 Tiết)

NỘI DUNG BÀI HỌC

Khoảng biến thiên và khoảng tứ vị phân

Phương sai và độ lệch chuẩn

Phát hiện số liệu bất thường hoặc không chính xác bằng biểu đồ hộp

TIẾT 1: KHOẢNG BIẾN THIÊN VÀ KHOẢNG TỨ PHÂN VỊ

1. Khoảng biến thiên và khoảng tứ vị phân

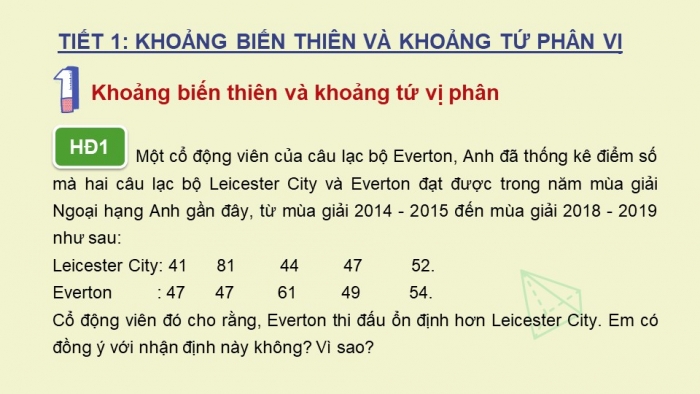
HĐ1

                 Một cổ động viên của câu lạc bộ Everton, Anh đã thống kê điểm số mà hai câu lạc bộ Leicester City và Everton đạt được trong năm mùa giải Ngoại hạng Anh gần đây, từ mùa giải 2014 - 2015 đến mùa giải 2018 - 2019 như sau:

Leicester City: 41      81         44         47          52.

Everton         : 47      47         61         49          54.

Cổ động viên đó cho rằng, Everton thi đấu ổn định hơn Leicester City. Em có đồng ý với nhận định này không? Vì sao?

Giải

Leicester City: 41      81         44         47          52.

Everton          : 47      47         61         49          54.

Nhận định này đúng vì:

• Leicester City có điểm lớn nhất là 81 và nhỏ nhất là 41 nên khoảng cách giữa điểm cao nhất và thấp nhất là 40.
• Everton có điểm lớn nhất là 61 và nhỏ nhất là 41 nên khoảng cách giữa điểm cao nhất và thấp nhất là 20.
• Khoảng cách giữa điểm cao nhất và thấp nhất của Everton là ít hơn.

KẾT LUẬN

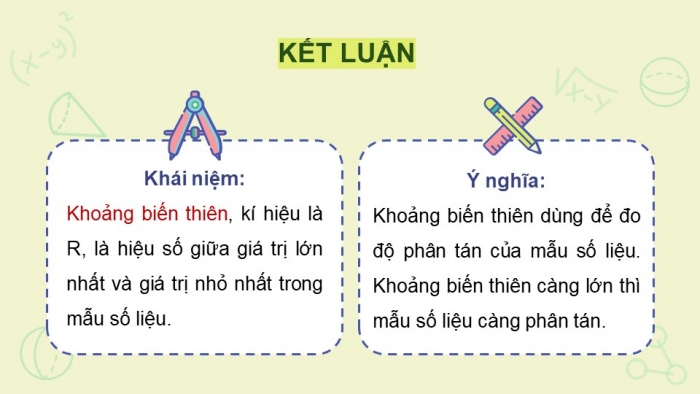
Khái niệm:

Khoảng biến thiên, kí hiệu là R, là hiệu số giữa giá trị lớn nhất và giá trị nhỏ nhất trong mẫu số liệu.

Ý nghĩa:

Khoảng biến thiên dùng để đo độ phân tán của mẫu số liệu. Khoảng biến thiên càng lớn thì mẫu số liệu càng phân tán.

Ví dụ 1

Điểm kiểm tra học kì môn Toán của các bạn Tổ 1, Tổ 2, lớp 10A được cho như sau:

Tổ 1:  7    8    8    9    8    8    8

Tổ 2: 10   6    8    9    9    7    8    7     8

1. Điểm kiểm tra trung bình của hai tổ có như nhau không?
2. Tính khoảng biến thiên của hai mẫu số liệu. Căn cứ trên chỉ số này, các bạn tổ nào học đều hơn?

Giải

8. a) Điểm kiểm tra trung bình của hai tổ đều bằng 8.
9. b) Đối với Tổ 1: Điểm kiểm tra thấp nhất, cao nhất tương ứng là 7; 9. Do đó, khoảng biến thiên là R₁: 9 - 7 = 2.

     Đối với Tổ 2: Điểm kiểm tra thấp nhất, cao nhất tương ứng là 6; 10. Do đó khoảng biến thiên là: R₂ = 10 - 6 = 4.

Do R₂ > R₁ nên ta nói các bạn Tổ 1 học đều hơn các bạn Tổ 2.

Luyện tập 1

Mẫu số liệu sau cho biết chiều cao (đơn vị cm) của các bạn trong tổ:

163       159       172        167        165          168          170          161.

Tính khoảng biến thiên của mẫu số liệu này.

Giải

Giá trị nhỏ nhất: 159.

Giá trị lớn nhất: 172.

Khoảng biến thiên: 172 – 159 = 13.

Nhìn vào khoảng biến thiên ta có thể đánh giá các giá trị khác không phải giá trị nhỏ nhất, giá trị lớn nhất không?

Nhận xét:

Sử dụng khoảng biến thiên có ưu điểm là đơn giản, dễ tính toán song khoảng biến thiên chỉ sử dụng thông tin của giá trị lớn nhất và giá trị nhỏ nhất mà bỏ qua thông tin từ tất cả các giá trị khác. Do đó, khoảng biến thiên rất dễ bị ảnh hưởng bởi các giá trị bất thường.

Thực hiện HĐ2 theo nhóm đôi.

HĐ2

               Trong một tuần, nhiệt độ cao nhất trong ngày (đơn vị ^oC) tại hai thành phố Hà Nội và Điện Biên được cho như sau:

Hà Nội:     23      25        28        28        32          33          35.

Điện Biên: 16      24        26        26        26           27          28.

1. a) Tính khoảng biến thiên của mỗi mẫu số liệu và so sánh.
2. b) Em có nhận xét gì về sự ảnh hưởng của giá trị 16 đến khoảng biến thiên của mẫu số liệu về nhiệt độ cao nhất trong ngày tại Điện Biên?
3. c) Tính các tứ phân vị và hiệu Q₃ - Q₁ cho mỗi mấu số liệu. Có thể dùng hiệu này để đo độ phân tán của mẫu số liệu không?

Giải

1. a) Hà Nội:

Khoảng biến thiên là: R₁ = 35 – 23 = 12

Điện biên:

Khoảng biến thiên là: R₂ = 28 – 16 = 12

1. b) Giá trị 16 làm khoảng biên thiên lớn hơn.

c)

• Hà Nội:

- Sắp xếp theo thứ tự không giảm: 23; 25; 28; 32; 33; 35

- Tứ phân vị là: Q₂ = 28; Q₁ = 25; Q₃ = 33. Ta có: Q₃ – Q₁ = 33 – 25 = 8.

• Điện Biên:

- Sắp xếp theo thứ tự không giảm: 16; 24; 26; 26; 26; 27; 28.

- Tứ phân vị là: Q₁ = 24; Q₂ = 26; Q₃ = 27. Ta có: Q₃ – Q₁ = 27 – 24 = 3.

Có thể dùng số liệu này để đo độ phân tán của số liệu.

Em hãy nêu định nghĩa và ý nghĩa của khoảng tứ phân vị.

KẾT LUẬN

Khoảng tứ phân vị, kí hiệu là ∆_Q, là hiệu số giữa tứ phân vị thứ ba và tứ phân vị thứ nhất, tức là:

 ∆_Q = Q₃ - Q₁

Khoảng tứ phân vị cũng là một số đo độ phân tán của mẫu số liệu. Khoảng tứ phân vị càng lớn thì mẫu số liệu càng phân tán.

Về bản chất, khoảng tứ phân vị là khoảng biến thiên của 50% số liệu chính giữa của mẫu số liệu.

Chú ý

Một số tài liệu gọi khoảng biến thiên là biên độ và khoảng tứ phân vị là độ trải giữa.

Ví dụ 2