Giáo án và PPT Toán 10 chân trời Bài 2: Dùng bảng tính để tính các số đặc trưng của mẫu số liệu thống kê

BÀI 2: DÙNG BẢNG TÍNH ĐỂ TÍNH CÁC SỐ ĐẶC TRƯNG 

CỦA MẪU SỐ LIỆU THỐNG KÊ ( 1 TIẾT)

A. HOẠT ĐỘNG KHỞI ĐỘNG (MỞ ĐẦU)

- GV tổ chức cho HS trả lời câu hỏi ôn lại kiến thức :

+ GV yêu cầu HS nhắc lại ý nghĩa và công thức tính số trung bình;

+Ý nghĩa của trung vị;

+Ý nghĩa của tứ phân vị;

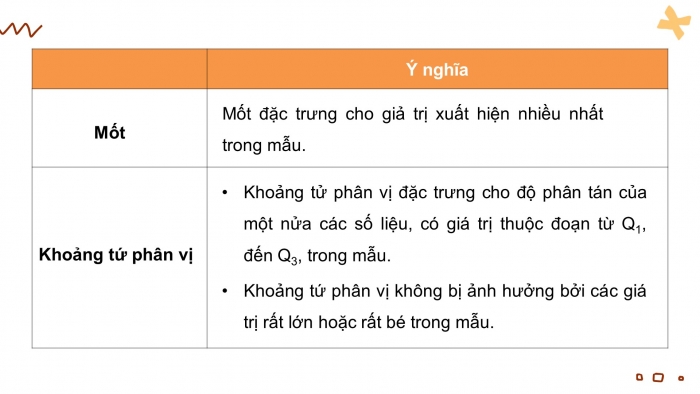
+Ý nghĩa của mốt, ý nghĩa củ khoảng tứ phân vị;

+Công thức tính phương sai; 

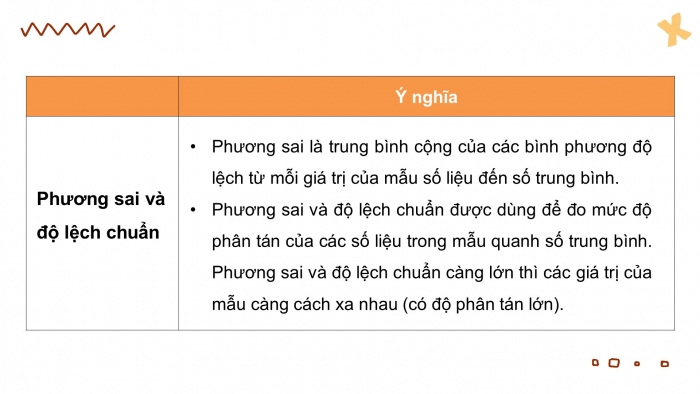
+ Ý nghĩa của phương sai và độ lệch chuẩn

B.HÌNH THÀNH KIẾN THỨC MỚI

Hoạt động 1: Nhập một mẫu dữ liệu thống kê vào các hàng và cột của một bảng tính trong bảng tính.

- GV hướng dẫn HS thực hiện bài tập Ví dụ : Nhập dữ liệu thống kê điểm kiểm tra môn Toán của 25 học sinh lớp 10A vào phần mềm bảng tính và lập bảng tần số như sau đây:

Sản phẩm dự kiến:

+ GV hướng dẫn và cho HS nhắc lại cách sử dụng hàm FREQUENCY để tạo bảng phân phối tần số giống như kết quả ở trên:

• Cấu trúc hàm FREQUENCY: = FREQUENCY(data_array, bins_array)

Trong đó: 

data_array: đối số bắt buộc, là mảng hoặc tham chiếu tới một tập giá trị mà bạn muốn đếm tần suất của nó.

bins_array: đối số bắt buộc, là mảng hoặc tham chiếu tới các khoảng mà bạn muốn nhóm các giá trị trong data_array vào trong đó.

Hoạt động 2: Tìm hiểu một số hàm số liệu thống kê trong bảng tính Exel và giải thích một số kết quả của bảng tính.

- GV cho HS thảo luận theo nhóm, yêu cầu HS nêu cấu trúc sử dụng hàm AVERAGE; MEDIAN; QUARTILE.EXC; MODE; VAR.P; STDEV.P và ý nghĩa của chúng. 

Sản phẩm dự kiến:

- Cấu trúc hàm Average là: =AVERAGE(number1,[number2],…).

Trong đó:

number1: đối số thứ nhất có thể là số, tham chiếu ô hoặc phạm vi chứa số mà ta muốn tính trung bình, bắt buộc.

number2: là các số, tham chiếu ô hoặc phạm vi chứa số bổ sung mà ta muốn tính trung bình tối đa 255 số, tùy chọn.

- Cấu trúc hàm Median: = MEDIAN(number1, [number2], ...)

Cú pháp hàm MEDIAN có các đối số dưới đây:

Number1, number2, ...    Number1 là bắt buộc, các số tiếp theo là tùy chọn. 1 tới 255 số mà ta muốn tìm trung vị.

- Cấu trúc hàm Quartile.exc:  = QUARTILE.EXC(array,quart)

Trong đó:

Array: Mảng hoặc phạm vi ô có chứa các giá trị số mà ta muốn tìm giá trị bắt buộc
Quart: Giá trị cần trả về. Giá trị bắt buộc.

- Cấu trúc hàm Mode: 

=MODE(number1,[number2],...)

Trong đó: Number1 là đối số bắt buộc, là dãy số liệu mà ta muốn tìm số giá trị có tần suất xuất hiện lớn nhất. Ta cũng có thể điền địa chỉ ô của vùng dữ liệu để Excel tham chiếu ô đến vùng dữ liệu đó.

- Cấu trúc hàm VAR.P: 

= VAR.P(NUMBER1,[NUMBER2],...)

Number1     Bắt buộc. Đối số dạng số đầu tiên tương ứng với tổng thể.

Number2, ...     Tùy chọn. Là các đối số dạng số từ 2 đến 254 tương ứng với một tập hợp.

- Cấu trúc hàm STDEV.P (hàm tính độ lệch chuẩn): 

= STDEVP(number1, [number2].)

Number1: Đối số dạng số đầu tiên tương ứng với tổng thể. Giá trị bắt buộc.
Number2: Đố số dạng số từ 2 đến 255 tương ứng với tổng thể.

C. HOẠT ĐỘNG LUYỆN TẬP

GV yêu cầu HS thực hiện bài tập trắc nghiệm.

Câu 1: Cho hai tập hợp A = {1; 2; a; b} và B = {1; x; y} với x, y khác a, b, 1, 2. Kết luận nào sau đây là đúng?

A. A ∩ B = B;

B. A ∩ B = ∅;

C. A ∩ B = A;

D. A ∩ B = {1}.

Câu 2: Trong các tập hợp sau đây, tập hợp nào bằng tập hợp M = ℝ\(-∞; 2):

A. A = (‒∞; - 2);

B. B = (‒∞; 2);

C. C = (2; +∞);

D. D = [2; +∞).

Câu 3: Trong các tập hợp sau, tập hợp nào bằng nhau:

A. A = {0; 2; 4; 6; 8}, B = {x| x ∈ ℕ, x chia hết cho 2 và x < 12};

B. A = {x| x ∈ ℕ, x ⋮ 2 và 2< x < 6}, B = {x| x ∈ ℕ, x chia hết cho 4 và 1 < x < 5};

C. A = {2; 4; 6; 8}, B = {x| x ∈ ℕ, x chia hết cho 2 và x < 10};

D. A = {x| x ∈ ℕ, x chia hết cho 3 và x < 12}, B = {x| x ∈ ℕ, x chia hết cho 4 và x < 12}.

Câu 4: Cho 3 tập hợp E, F, G sao cho E ⊂ F, F ⊂ G và G ⊂ E. Câu nào sau đây đúng?

A. G ⊂ F;

B. E ⊂ G;

C. E = G;

D. E = F = G.

Câu 5: Cho hai tập hợp A ={1;2;3;7;9}và B ={1;2;7;10}. Tập hợp A ∪ Bcó bao nhiêu phần tử?

A. 4;

B. 3;

C. 5;

D. 6.

Gợi ý đáp án:

D. HOẠT ĐỘNG VẬN DỤNG

GV yêu cầu HS hoạt động hoàn thành bài tập trong sgk.