Trắc nghiệm câu trả lời ngắn Toán 12 cánh diều Bài 1: Tính đơn điệu của hàm số

BÀI 1. TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ

Câu 1: Cho hàm số liên tục trên và có đồ thị như Hình vẽ. Hàm số đã cho có bao nhiêu điểm cực trị?

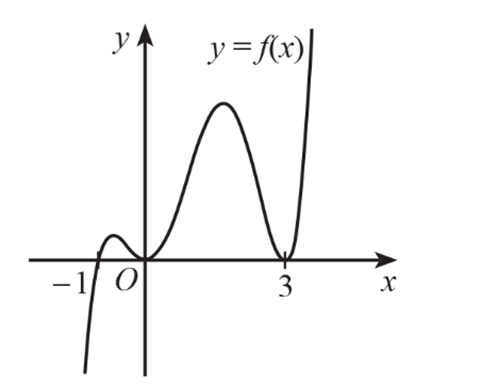
• 4

Câu 2: Giả sử sự lây lan của một loại virus ở một địa phương có thể được mô hình hoá bằng hàm số , trong đó là số người bị nhiễm bệnh (đơn vị là trăm người) và t là thời gian (tuần). Gọi là khoảng thời gian lâu nhất mà số người bị nhiễm bệnh tăng lên. Tính giá trị  

• -64

Câu 3: Một con cá hồi bơi ngược dòng để vượt khoảng cách là 300 km. Vận tốc dòng nước là 6 km. Nếu vận tốc bơi của cá khi nước đứng yên là v (km/h) thì năng lượng tiêu hao của cá trong t giờ được cho bởi công thức , trong đó c là hằng số và E tính bằng Jun. Vận tốc bơi của cá khi nước đứng yên nằm ở khoảng thì  năng lượng tiêu hao của cá giảm. Tính giá trị .

• 15

Câu 4: Cho hàm số với m là tham số. Gọi S là tập hợp tất cả các giá trị nguyên của để hàm số nghịch biến trên khoảng . Tìm số phần tử của S.

• 3

Câu 5: Cho hàm số có bảng biến thiên như sau:

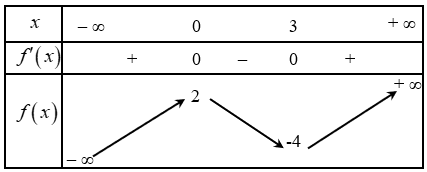
Đồ thị hàm số có điểm cực tiểu là . Tính giá trị của

• -1

Câu 6: Cho hàm số . Hàm số liên tục và có đồ thị trên như hình vẽ

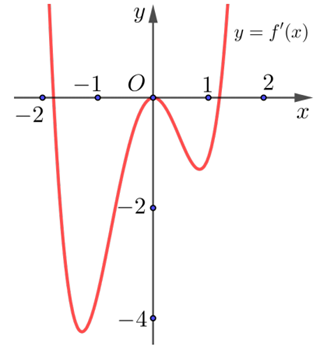
Giả sử hàm số nghịch biến trên khoảng Trong khoảng có nhiếu nhất bao nhiêu giá trị nguyên nhỏ hơn 2025?

• 3

Câu 7: Kính viễn vọng không gian Hubble được đưa vào vũ trụ ngày bằng tàu con thoi Discovery. Vận tốc của tàu con thoi trong sứ mệnh này, từ lúc cất cánh tại thời điểm cho đến khi tên lửa đẩy được phóng đi tại thời điểm cho bởi hàm số sau: ( được tính theo đơn vị ft/s, )

Biết rằng gia tốc của tàu con thoi sẽ tăng trong khoảng thời gian từ giây đến giây tính từ thời điểm cất cánh cho đến khi tên lửa đẩy được phóng đi. Khi đó tính giá trị .

• 103

BÀI TẬP THAM KHẢO THÊM

Câu hỏi 1: Cho hàm số y = f (x) có bảng biến thiên như sau:

Hàm số đã cho nghịch biến trên khoảng nào ?

Trả lời: Đồng biến (0;1)

Câu hỏi 2: Điền vào chỗ trống:

Cho hàm số y = f(x) có đạo hàm trên tập K⊂R, với K là một khoảng, nửa khoảng hoặc đoạn.

• Nếu f′(x) > 0, ∀x ∈ K thì hàm số y = f(x) _____ trên K.

• Nếu _____, ∀x∈K thì hàm số y = f(x) nghịch biến trên K. 

Trả lời: đồng biến; f′(x) < 0

Câu hỏi 3: Đúng/sai:

Giả sử hàm số y = f(x) liên tục trên khoảng (a;b) chứa điểm x₀​, và có đạo hàm trên các khoảng (a;x₀) và (x₀;b). Khi đó:

1. Nếu f′(x)<0 với mọi x∈(a;x₀) và f′(x)>0 với mọi x∈(x₀;b) thì hàm số f(x) đạt cực tiểu tại điểm x₀.

2. Nếu f′(x)>0 với mọi x∈(a;x₀) và f′(x)<0 với mọi x∈(x₀;b) thì hàm số f(x) đạt cực tiểu tại điểm x₀​.

Trả lời: 1. Đúng    2. Sai: Cực tiểu -> cực đại

Câu hỏi 4: Cho hàm số y = f (x) có đồ thị như hình vẽ bên. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

Trả lời:  (0;1)

Câu hỏi 5: Cho hàm số y=f(x)  có bảng xét dấu đạo hàm như sau. Số điểm cực trị của hàm số đã cho là?

Trả lời: 4

Câu hỏi 6: Cho hàm số y = f (x) có đồ thị như hình vẽ bên 

Số cực trị cả đồ thị hàm số y = f(|x|) ?

Trả lời:  ......................................

Câu hỏi 7: Quan sát bảng biến thiên:

Tìm giá trị cực tiểu của hàm số trên

Trả lời: ......................................

Câu hỏi 8: Nếu hàm số y= f(x) đồng biến trên khoảng (0; 2) thì hàm số y= f(2x) đồng biến trên khoảng nào?

Trả lời: ......................................

Câu hỏi 9: Cho hàm số y = f(x) xác định, liên tục trên R  và có đồ thị là đường cong trong hình vẽ bên. 

Hàm số đã cho nghịch biến trên khoảng?

Trả lời:  ......................................

Câu hỏi 10: Cho hàm số y = f(x) có đồ thị như hình vẽ bên:

Hàm số đã cho nghịch biến, đồng biến trên khoảng?

Trả lời: ......................................

Câu hỏi 11: Cho hàm số y = f(x) có đồ thị như hình vẽ bên:

Tìm điểm cực trị cả đồ thị hàm số y = f(x)

Trả lời: ......................................

Câu hỏi 12: Hàm số f(x) có đạo hàm trên R là hàm số f′(x). Biết đồ thị hàm số f′(x) được cho như hình vẽ.

Xét tính đúng sai của các mệnh đề sau và sửa lại:

a) Hàm số đạt cực tiểu tại x=0

b) Hàm số nghịch biến trên khoảng (0;1)

Trả lời: ......................................

Câu hỏi 13: Chọn f(x₁) < f(x₂); f(x₁) > f(x₂) để điền vào chỗ trống:

Cho hàm số f(x) xác định trên (a;b), với x₁; x₂ bất kỳ thuộc (a;b), ta có:

Hàm số f(x) đồng biến trên (a; b) khi và chỉ khi x₁ < x₂ ⇔ ____

Hàm số f(x) nghịch biến trên (a; b) khi và chỉ khi x₁ < x₂ ⇔ ___

Trả lời: ......................................

Câu hỏi 14: Hỏi hàm số y =  nghịch biến trên khoảng nào ?

Trả lời:  ......................................

Câu hỏi 15: Cho hàm số y = x +  có mấy điểm cực trị ? 

Trả lời: ......................................

Câu hỏi 16: Cho hàm số y =  có bao nhiêu cực đại ? 

Trả lời: ......................................

Câu hỏi 17: Tìm hiệu số giữa giá trị cực đại và giá trị cực tiểu của hàm số: 

y = – 3x² + 4
Trả lời: ......................................

Câu hỏi 18: Cho hàm số y=ax³+bx²+cx+d. Nếu đồ thị hàm số có 2 điểm cực trị là gốc tọa độ và điểm A(−1;−1), thì hàm số có phương trình là gì ?

Trả lời:  ......................................

Câu hỏi 19: Cho hàm số y = f(x) liên tục trên R và biết f(x) có đạo hàm  f′(x) và  hàm số y = f(x) có đồ thị như hình vẽ

Xét trên (-) tìm khoảng nghịch biến cả hàm f(x) ?

Trả lời: ......................................

Câu hỏi 20: Hàm số f(x) có đạo hàm  f′(x) trên khoảng K. Hình vẽ bên là đồ thị cả hàm số f’(x) trên khoảng K

Hàm số f(x) có bao nhiêu điểm cực trị?

 Trả lời: ......................................

----------------------------------

----------------------- Còn tiếp -------------------------