Trắc nghiệm câu trả lời ngắn Toán 12 cánh diều Bài 3: Biểu thức tọa độ của các phép toán vectơ
Tài liệu trắc nghiệm dạng câu trả lời ngắn Toán 12 cánh diều Bài 3: Biểu thức tọa độ của các phép toán vectơ. Dựa trên kiến thức của bài học, bộ tài liệu được biên soạn chi tiết, đúng trọng tâm và rõ ràng. Câu hỏi đa dạng với các mức độ khó dễ khác nhau. Tài liệu có file Word tải về. Thời gian tới, nội dung này sẽ tiếp tục được bổ sung.
Xem: => Giáo án toán 12 cánh diều
BÀI 3. BIỂU THỨC TỌA ĐỘ CỦA CÁC PHÉP TOÁN VECTO
Câu 1:Trong không gian với hệ trục tọa độ ![]() cho hình thang
cho hình thang ![]() vuông tại
vuông tại ![]() và
và ![]() . Ba đỉnh
. Ba đỉnh ![]() Hình thang có diện tích bằng
Hình thang có diện tích bằng ![]() . Giả sử đỉnh
. Giả sử đỉnh ![]() tính giá trị
tính giá trị ![]() .
.
6
Câu 2: Một chiếc xe đang kéo căng sợi dây cáp ![]() trong công trường xây dựng, trên đó đã thiết lập hệ toạ độ
trong công trường xây dựng, trên đó đã thiết lập hệ toạ độ ![]() như hình vẽ dưới với độ dài đơn vị trên các trục tọa độ bằng
như hình vẽ dưới với độ dài đơn vị trên các trục tọa độ bằng ![]() . Tìm được tọa độ của vectơ
. Tìm được tọa độ của vectơ ![]() . Khi đó tính
. Khi đó tính ![]() . (Lấy kết quả đến chữ số thập phân thứ nhất)
. (Lấy kết quả đến chữ số thập phân thứ nhất)
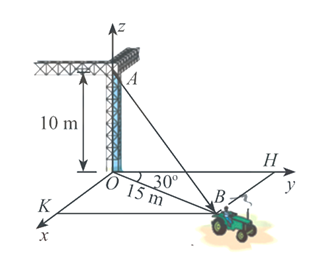
-2,5
Câu 3: Một chậu hoa được treo như hình vẽ. Biết rằng ba sợi dây có ba lực ![]() ,
,![]() ,
,![]() có độ lớn bằng
có độ lớn bằng ![]() . Biết sợi dây thứ hai hợp với sợi dây thứ nhất và sợi dây thứ ba đều bằng
. Biết sợi dây thứ hai hợp với sợi dây thứ nhất và sợi dây thứ ba đều bằng ![]() , sợi dây thứ nhất hợp với sợi dây thứ ba góc
, sợi dây thứ nhất hợp với sợi dây thứ ba góc ![]() . Tính độ lớn của hợp lực
. Tính độ lớn của hợp lực ![]() ,
,![]() ,
,![]() . (Làm tròn kết quả đến chữ số thập phân thứ nhất)
. (Làm tròn kết quả đến chữ số thập phân thứ nhất)

33,5
Câu 4: Trong không gian ![]() cho hai véc tơ
cho hai véc tơ ![]() và
và ![]() thỏa mãn
thỏa mãn ![]() . Gọi
. Gọi ![]() là tập tất cả các giá trị của tham số
là tập tất cả các giá trị của tham số ![]() . Khi đó tổng các phần tử của
. Khi đó tổng các phần tử của ![]() bằng bao nhiêu.
bằng bao nhiêu.
-2
Câu 5: Trong không gian tọa độ ![]() , cho điểm
, cho điểm ![]() Gọi
Gọi ![]() là điểm khác
là điểm khác ![]() và không trùng với các điểm
và không trùng với các điểm ![]() sao cho
sao cho ![]() . Khi đó, tính giá trị của
. Khi đó, tính giá trị của ![]() (Làm tròn kết quả đến chữ số thập phân thứ nhất).
(Làm tròn kết quả đến chữ số thập phân thứ nhất).
-3,3
Câu 6: Trong không gian với hệ trục tọa độ cho trước, một vệ tinh bắt đầu từ tọa độ ![]() và đang di chuyển trong không gian với vectơ vận tốc
và đang di chuyển trong không gian với vectơ vận tốc ![]() . Sau 10 giây, vệ tinh thay đổi hướng và di chuyển theo vectơ mới
. Sau 10 giây, vệ tinh thay đổi hướng và di chuyển theo vectơ mới ![]() trong 5 giây. Tọa độ cuối cùng của vệ tinh là
trong 5 giây. Tọa độ cuối cùng của vệ tinh là ![]() Tính
Tính ![]()
246
BÀI TẬP THAM KHẢO THÊM
Câu 1: Trong không gian với hệ tọa độ Oxyz, cho vecto ![]() (3;0;1);
(3;0;1); ![]() (2;1;0). Tính
(2;1;0). Tính ![]()
Trả lời: ![]() = 6
= 6
Câu 2: Trong không gian Oxyz , cho hai vectơ ![]() = (2;-3;3);
= (2;-3;3); ![]() = (0;2;-1) và
= (0;2;-1) và ![]() = (3;-1;5). Tìm vecto
= (3;-1;5). Tìm vecto ![]() 2
2![]()
Trả lời: (-2;2;-7)
Câu 3: Trong không gian với hệ tọa độ Oxyz, cho hai véc tơ ![]() = (-1;3;-2);
= (-1;3;-2); ![]() = (2;5;-1). Tìm tọa độ của véc tơ
= (2;5;-1). Tìm tọa độ của véc tơ ![]() = 2
= 2![]() - 3
- 3![]()
Trả lời: ![]() = (-8;-9;-1)
= (-8;-9;-1)
Câu 4: Trong không gian Oxyz, cho hai vectơ ![]() = (1;–4;0) và
= (1;–4;0) và ![]() = (–1;–2;1). Tính vectơ
= (–1;–2;1). Tính vectơ ![]() .
.
Trả lời: (–2;–10;3)
Câu 5: Trong không gian với một hệ trục toạ độ cho trước, ra đa phát hiện một chiếc máy bay di chuyển với vận tốc và hướng không đổi từ điểm A(800;500;7) đến điểm B(940;550;8) trong 10 phút. Nếu máy bay tiếp tục giữ nguyên vận tốc và hướng bay thì toạ độ của máy bay sau 5 phút tiếp theo là gì?
Trả lời: C(1010;575;8,5)
Câu 6: Trong không gian với hệ trục tọa độ Oxyz, cho ![]() = (2;–3;3),
= (2;–3;3), ![]() = (0;2;-1) và
= (0;2;-1) và ![]() = (3;-1;5). Tìm tọa độ của vectơ
= (3;-1;5). Tìm tọa độ của vectơ ![]() -3
-3![]()
Trả lời: ………………………………………
Câu 7: Trong không gian với hệ trục tọa độ Oxyz, cho ![]() = (1;–2;3),
= (1;–2;3), ![]() = (-2;1;2). Tính tích vô hướng (
= (-2;1;2). Tính tích vô hướng (![]() +
+ ![]() ).
). ![]()
Trả lời: ………………………………………
Câu 8: Trong không gian với hệ trục tọa độ Oxyz, cho hình hộp ABCD.A’B’C’D’ có ![]() = (1;0;1),
= (1;0;1), ![]() = (2;1;2),
= (2;1;2), ![]() = (1;-1;1) và
= (1;-1;1) và ![]() = (1;1;-1). Tính tọa độ
= (1;1;-1). Tính tọa độ ![]()
Trả lời: ………………………………………
Câu 9: Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A (2;-1;5); ![]() (5;-5;7) ;M (x;y;1). Với giá trị nào của x, y thì A,B,M thẳng hàng
(5;-5;7) ;M (x;y;1). Với giá trị nào của x, y thì A,B,M thẳng hàng
Trả lời: ………………………………………
Câu 10: Cho vecto ![]() = (1;-1;0), cùng phương với vecto
= (1;-1;0), cùng phương với vecto ![]() = (2;2k-1;0) với k =
= (2;2k-1;0) với k =![]() với
với ![]() là phân số tối giản và n > 0. Tính m + n
là phân số tối giản và n > 0. Tính m + n
Trả lời: ………………………………………
Câu 11: Trong không gian với hệ trục tọa độ Oxyz, cho ![]() = (1;–7;9),
= (1;–7;9), ![]() = (3;-6;1),
= (3;-6;1), ![]() = (2;1;-7). Biểu tdiễn vecto
= (2;1;-7). Biểu tdiễn vecto ![]() = (-4;13;-6) theo các vecto
= (-4;13;-6) theo các vecto ![]() ;
; ![]() ;
; ![]() ta được
ta được ![]() = x
= x![]() . Tính x + y + z
. Tính x + y + z
Trả lời: ………………………………………
Câu 12: Trong không gian tọa độ Oxyz cho ba điểm A(2;5;1), B(–2;–6;2), C(1;2;–1) và điểm M(m;m;m), để |![]() đạt giá trị nhỏ nhất thì m bằng bao nhiêu?
đạt giá trị nhỏ nhất thì m bằng bao nhiêu?
Trả lời: ………………………………………
Câu 13: Trong không gian với hệ trục tọa độ Oxyz, cho ![]() = (2;–1;1) và
= (2;–1;1) và ![]() =(0;–3;–m). Tìm số thực m sao cho tích vô hướng
=(0;–3;–m). Tìm số thực m sao cho tích vô hướng ![]() = 1.
= 1.
Trả lời: ………………………………………
Câu 14: Trong không gian tọa độ Oxyz cho ba điểm A(-1;2;-3), B(0;2;1), C(-1;2;1) và điểm M thuộc Oy. Tìm giá trị nhỏ nhất cả biểu thức |![]()
Trả lời: ………………………………………
Câu 15: Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(2;2;0),B(2;0;–2) và điểm M(a,b,c) với a,b,c là các số thực thay đổi thỏa mãn a + 2b – c – 1 = 0. Biết MA = MB và góc AMB có số đo lớn nhất. Tính S = a + 2b + 3c
Trả lời: ………………………………………
Câu 16: Trong không gian Oxyz với ![]() lần lượt là các vecto đơn vị trên các trục Ox,Oy,Oz. Tính tọa độ của vecto
lần lượt là các vecto đơn vị trên các trục Ox,Oy,Oz. Tính tọa độ của vecto ![]()
Trả lời: ………………………………………
Câu 17: Trong không gian với hệ tọa độ Oxyz, cho ![]() = (2;1;0) và
= (2;1;0) và ![]() =(-1;0;–2). Tính cos (
=(-1;0;–2). Tính cos (![]() ;
; ![]() )
)
Trả lời: ………………………………………
Câu 18: Cho hình chóp O.ABC có ba cạnh OA, OB , OC đôi một vuông góc và OA = OB = OC = a. Gọi M là trung điểm cạnh AB. Tính góc tạo bởi hai vectơ ![]()
Trả lời: ………………………………………
Câu 19: Trong không gian với hệ tọa độ Oxyz, cho A(2;0;0), B(0;2;0) , C(0;0;2). Có tất cả bao nhiê điểm M trong không gian thỏa mãn M không trùng với các điểm A, B, C và ![]() =
= ![]() =
= ![]() = 900
= 900
Trả lời: ………………………………………
Câu 20: Trong không gian với hệ trục tọa độ Oxyz cho hình thang ABCD vuông tại A và B . Ba đỉnh A(1;2;1), B(2;0;–1),C(6;1;0). Hình thang có diện tích bằng 6![]() . Giả sử đỉnh D(a;b;c). Tính a + b + c
. Giả sử đỉnh D(a;b;c). Tính a + b + c
Trả lời: ………………………………………
----------------------------------
----------------------- Còn tiếp -------------------------
=> Giáo án Toán 12 cánh diều Bài 3: Biểu thức tọa độ của các phép toán vectơ
