Giáo án điện tử chuyên đề Toán 12 cánh diều Bài 2: Vận dụng đạo hàm để giải quyết một số bài toán tối ưu trong thực tiễn
Tải giáo án điện tử Chuyên đề học tập Toán 12 cánh diều Bài 2: Vận dụng đạo hàm để giải quyết một số bài toán tối ưu trong thực tiễn. Bộ giáo án chuyên đề được thiết kế sinh động, đẹp mắt. Thao tác tải về đơn giản, dễ dàng sử dụng và chỉnh sửa. Thầy, cô kéo xuống để xem chi tiết.
Xem: => Giáo án toán 12 cánh diều
Click vào ảnh dưới đây để xem 1 phần giáo án rõ nét










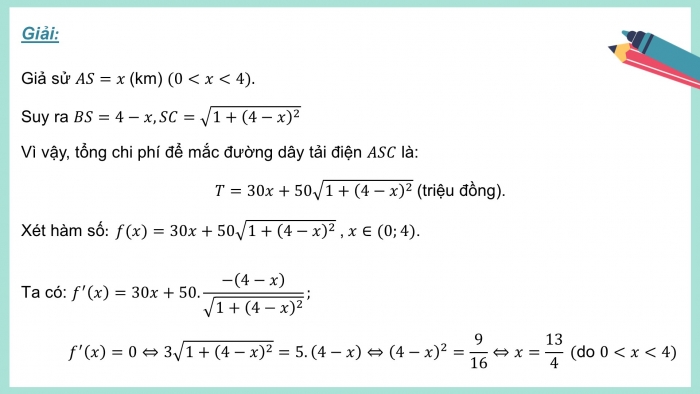
Xem toàn bộ: Giáo án điện tử chuyên đề toán 12 cánh diều
CHÀO MỪNG TẤT CẢ CÁC EM ĐẾN VỚI MÔN TOÁN!
KHỞI ĐỘNG
Để giảm huyết áp của một bệnh nhân được cho bởi công thức , trong đó là liều lượng thuốc được tiêm cho bệnh nhân ( được tính bằng miligam)
Câu hỏi: Liều lượng thuốc cần tiêm cho bệnh nhân là bao nhiêu để huyết áp giảm nhanh nhất?
BÀI 2. VẬN DỤNG ĐẠO HÀM ĐỂ GIẢI QUYẾT MỌT SỐ BÀI TOÁN TỐI ƯU TRONG THỰC TIỄN
CHƯƠNG II. ỨNG DỤNG TOÁN HỌC ĐỂ GIẢI QUYẾT MỘT SỐ BÀI TOÁN TỐI ƯU
I
Vận dụng đạo hàm để giải quyết một số bài toán tối ưu trong khoa học, kĩ thuật và công nghệ
Vận dụng đạo hàm để giải quyết một số bài toán tối ưu trong kinh tế
II
NỘI DUNG BÀI HỌC
I. VẬN DỤNG ĐẠO HÀM ĐỂ GIẢI QUYẾT MỘT SỐ BÀI TOÁN TỐI ƯU TRONG KHOA HỌC, KĨ THUẬT VÀ CÔNG NGHỆ
Bài toán 1. Hãy giải bài toán ở phần mở đầu.
Giải:
Ta có:
Do đó,
Bảng biến thiên của hàm số:
Căn cứ bảng biến thiên, ta có: tại .
Vậy liều lượng thuốc cần tiêm cho bệnh nhân để huyết áp giảm nhanh nhất là 20 mg.
Bài toán trở thành: Tìm giá trị lớn nhất của hàm số trên đoạn
Bài toán 2. Trong 25 ngày đầu tiên sau khi phát hiện một bệnh dịch, các chuyên gia y tế ước tính số người nhiễm bệnh (kể từ ngày xuất hiện bệnh nhân thứ nhất) đến ngày thứ là: (Nguồn: Giải tích 12 Nâng cao, NXBGD Việt Nam, 2020).
a) Số người nhiễm bệnh (kể từ ngày xuất hiện bệnh nhân đầu tiên) lớn nhất là bao nhiêu?
b) Nếu coi là hàm số xác định trên đoạn thì được xem là tốc độ truyền bệnh (người/ngày) tại thời điểm . Xác định ngày mà tốc độ truyền bệnh là lớn nhất và tính tốc độ đó.
Giải:
Ta có:
Căn cứ bảng biến thiên, ta có: tại .
Vậy sau 25 ngày kể từ ngày xuất hiện bệnh nhân đầu tiên, số người nhiễm bệnh lớn nhất là 12 500 người.
a) Bài toán trở thành: Tìm giá trị lớn nhất của hàm số trên đoạn
Do đó, Suy ra trên đoạn
Bảng biến thiên của hàm số:
Giải:
Ta có: . Do đó,
Căn cứ bảng biến thiên, ta có: tại .
Vậy tốc độ truyền bệnh lớn nhất là người/ngày và đạt được tại ngày thứ .
b) Bài toán trở thành: Tìm giá trị lớn nhất của hàm số trên đoạn
Bảng biến thiên của hàm số:
Bài toán 3. Người ta thiết kế một đường dây tải điện nối từ trạm biến áp ở vị trí A đến trạm biến áp ở vị trí C. Do điều kiện thực tế nên phương ánthiết kế được đưa ra như sau:
- Chọn điểm sao cho
- Chọn một ví trí là điểm nằm giữa và để mắc đường dây tải điện đi từ đến , rồi từ đến như ở Hình 1.
Giải:
Giả sử (km)
Suy ra
Vì vậy, tổng chi phí để mắc đường dây tải điện là:
(triệu đồng).
Xét hàm số , .
Giải:
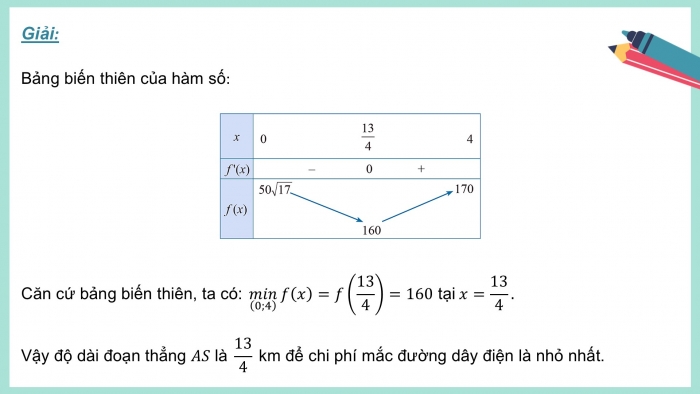
Bảng biến thiên của hàm số:
Luyện tập 1
Một nhà máy cần sản xuất một bể nước không nắp bằng tôn có dạng hình
hộp chữ nhật với đáy có chiều dài gấp hai lần chiều rộng và thể tích là
Tính chiều rộng của đáy hình hộp chữ nhật đó sao cho số tôn cần sử dụng là nhỏ nhất.
Giải:
Gọi chiều rộng của đáy hình hộp chữ nhật đó là .
Chiều dài của đáy hình hộp chữ nhật đó là
Diện tích đáy hình hộp chữ nhật đó là
Ta có: .
Bảng biến thiên của hàm số:
Dựa vào bảng biến thiên, ta có: .
Vậy chiều rộng của đáy hình hộp chữ nhật là 1 mét để số tôn cần sử dụng là nhỏ nhất.
Giải:
II. VẬN DỤNG ĐẠO HÀM ĐỂ GIẢI QUYẾT MỘT SỐ BÀI TOÁN TỐI ƯU TRONG KINH TẾ
Bài toán 4. Giả sử lợi nhuận của doanh nghiệp khi sản xuất sản phẩm là với có đạo hàm tại mọi điểm trên khoảng
Khi đó, lợi nhuận gia tăng khi sản xuất thêm 1 sản phẩm (từ sản phẩm lên sản phẩm) là hiệu hiệu này còn được gọi là giá trị cận biên tại . Lợi nhuận cận biên khi sản xuất sản phẩm, kí hiệu: , được xác định bởi
b) Giả sử hàm lợi nhuận cận biên giảm dần khi càng lớn. Nêu nhận xét về hàm giá trị cận biên khi càng lớn.
Giải:
Do đó, ta có thể lấy là giá trị xấp xỉ của giá trị cận biên tại
Vậy ta có thể lấy một giá trị xấp xỉ của giá trị cận biên tại là
b) Do và giảm dần khi càng lớn nên ta có thể thấy rằng hàm giá trị cận biên cũng giảm khi càng lớn.
Nhận xét
Quy luật lợi nhuận cận biên giảm dần nói rằng khi càng lớn thì giá trị cận biên càng nhỏ. Nói cách khác, khi lợi nhuận cận biên bắt đầu giảm dần đối với một loại hàng hoá thì việc sản xuất thêm loại hàng hoá đó sẽ làm giảm lợi nhuận cho doanh nghiệp.
Bài toán 5. Một doanh nghiệp sản xuất một loại sản phẩm. Giả sử tổng chi phí (đơn vị: triệu đồng) để sản xuất và bán hết sản phẩm đó được cho bởi:
Giả sử tổng số tiền doanh nghiệp thu được (đơn vị: triệu đồng) khi bán hết sản phẩm đó là:
(Nguồn: R. Larson and B. Edwards, Calculus 10e, Cengage 2014).
a) Tính số tiền lãi doanh nghiệp thu được khi bán hết sản phẩm đó. Từ đó, hãy cho biết doanh nghiệp cần sản xuất bao nhiêu sản phẩm để số tiền lãi thu được là lớn nhất.
b) Tỉ số được gọi là chi phí trung bình cho một sản phẩm khi bán ra. Hãy cho biết doanh nghiệp cần sản xuất bao nhiêu sản phẩm để chi phí trung bình là nhỏ nhất.
Giải:
a) Số tiền lãi doanh nghiệp thu được khi bán hết sản phẩm là:
Xét hàm với .
Ta có:
Bảng biến thiên của hàm số:
Căn cứ bảng biến thiên, ta có: tại
Vậy doanh nghiệp cần sản xuất sản phẩm để số tiền lãi thu được là lớn nhất.
Giải:
Bảng biến thiên của hàm số:
Căn cứ bảng biến thiên, ta có: tại
Vậy doanh nghiệp cần sản xuất sản phẩm để chi phí trung bình là nhỏ nhất.
Bài toán 6. Một cửa hàng nhập bưởi da xanh với giá nhập là 150 000 đồng/1 quả và bán bưởi đó với giá bán là 200 000 đồng/1 quả. Với giá bán này thì cửa hàng dự kiến chỉ bán được 50 quả. Cửa hàng này quyết định giảm giá bán. Biết rằng nếu cửa hàng cứ giảm mỗi quả 10 000 đồng thì số bưởi bán được tang thêm là 50 quả. Xác định giá bán bưởi để cửa hàng đó thu được lợi nhuận lớn nhất.
Giải:
Gọi là số lần giảm giá bán bưởi
Số tiền giảm giá cho mỗi quả bưởi là
Khi đó, giá bán của mỗi quả bưởi là và số bưởi bán được là
Lợi nhuận cửa hàng thu được là:
Xét hàm với
Ta có:
Bảng biến thiên của hàm số:
Giải:
Căn cứ bảng biến thiên, ta có: tại .
Vậy cửa hàng cần bán bưởi với giá đồng/1 quả để số tiền lãi thu được là lớn nhất.
Kết luận
Để giải quyết bài toán tối ưu trong thực tiễn bằng phương pháp sử dụng đạo hàm, ta có thể làm như sau:
Bước 1. Xây dựng hàm số biểu thị đại lượng biến thiên trong bài toán tối ưu đó.
Bước 2. Sử dụng đạo hàm để tìm giá trị lớn nhất, hoặc nhỏ nhất của hàm số nhận được ở Bước 1.
Bước 3. Dựa trên giá trị lớn nhất (hoặc nhỏ nhất) của hàm số nhận được ở Bước 2, ta có thể xác định được nghiệm cho bài toán tối ưu ban đầu.
Luyện tập 2
Một công ty có 50 căn phòng cho thuê. Biết rằng nếu công ty cho thuê mỗi căn phòng với giá 2 triệu đồng/1 tháng thì mọi căn phòng đều có người thuê, nhưng cứ mỗi lần tăng giá cho thuê mỗi căn phòng 100 000 đồng/1 tháng thì có thêm hai căn phòng bị bỏ trống. Công ty phải cho thuê mỗi căn phòng với giá là bao nhiêu để tổng số tiền thu được là lớn nhất?
Giải:
Đổi 100000 đồng = 0,1 triệu đồng.
Gọi là số lần tăng giá phòng
Số tiền tăng giá trong 1 tháng cho mỗi phòng là: (triệu đồng).
Khi đó, giá cho thuê của mỗi căn phòng trong 1 tháng là: (triệu đồng) và số phòng cho thuê được là: .
Tổng số tiền thu được là: (triệu đồng).
Xét hàm số , với .
Ta có: .
Bảng biến thiên của hàm số:
Giải:
Căn cứ bảng biến thiên, ta có
.
Vậy công ty phải cho thuê mỗi căn phòng với giá là triệu đồng để tổng số tiền thu được là lớn nhất.
LUYỆN TẬP
TRÒ CHƠI
NÔNG TRẠI VUI VẺ
Câu 1: Khi nuôi cá thí nghiệm trong hồ, một nhà khoa học đã nhận thấy rằng: nếu trên mỗi đơn vị diện tích của mặt hồ có con cá thì trung bình mỗi con cá sau một vụ cân nặng là . Hỏi phải thả bao nhiêu con cá trên một đơn vị diện tích của mặt hồ để sau một vụ thu hoạch được nhiều cá nhất?
A. 14 con
C. 12 con
Câu 2: Một công ty sản xuất ước tính chi phí sản xuất (tính bằng triệu đồng) cho sản phẩm được sản xuất là . Để giảm chi phí sản xuất trên mỗi sản phẩm, công ty cần tìm số sản phẩm tối ưu sao cho chi phí bình quân mỗi sản phẩm là thấp nhất. Số sản phẩm tối ưu để chi phí bình quân mỗi sản phẩm là thấp nhất là:
A. 4
C. 6
Câu 3: Một nhà máy đang sản xuất hàng hóa với số lượng sản phẩm và lợi nhuận (tính bằng triệu đồng) được mô tả bằng hàm . Để tối đa hóa lợi nhuận, số sản phẩm tối ưu cần sản xuất là:
A. 4
C. 7
Câu 4: Một người tiêu dùng mua một sản phẩm với giá , trong đó là số lượng sản phẩm mua. Để tối đa hóa tổng chi tiêu của người tiêu dùng, người đó cần mua bao nhiêu sản phẩm nếu tổng chi tiêu là hàm bậc hai của số lượng sản phẩm:
25 sản phẩm
C. 40 sản phẩm
30 sản phẩm
50 sản phẩm
A. 25 sản phẩm
Câu 5: Một công ty muốn tối ưu hóa diện tích sản xuất trong một khu vực có hình chữ nhật. Diện tích của khu vực được mô tả bởi hàm (tính bằng mét vuông), với là chiều dài và là chiều rộng. Nếu chiều dài được cố định ở mức 10 mét và chiều rộng thay đổi, chiều rộng tối ưu để đạt diện tích tối đa là:
A. 5 mét
C. 15 mét
Trò chơi kết thúc, mời các em cùng chuyển sang nội dung tiếp theo!
Trắc nghiệm đúng sai
Câu 1:
a) Trong bài toán tối ưu hóa sản xuất, nếu hàm chi phí sản xuất là thì giá trị của tại điểm cực tiểu của hàm chi phí là .
b) Một công ty muốn tối ưu hóa thiết kế của một sản phẩm để đạt được lợi nhuận tối đa. Nếu hàm lợi nhuận là thì điểm cực đại của lợi nhuận là .
c) Trong một hệ thống điều khiển nhiệt độ, hàm chi phí năng lượng có dạng Để tối ưu hóa chi phí năng lượng, giá trị tối ưu của nhiệt độ bằng 4.
d) Trong việc tối ưu hóa thiết kế cánh máy bay, hàm lực nâng có dạng . Điểm cực đại của hàm lợi nhuận là
------------------------------
----------------- Còn tiếp ------------------
Trên chỉ là 1 phần của giáo án. Giáo án khi tải về có đầy đủ nội dung của bài. Đủ nội dung của học kì I + học kì II
Đủ kho tài liệu môn học
=> Tài liệu sẽ được gửi ngay và luôn
Cách tải:
- Bước 1: Chuyển phí vào STK: 1214136868686 - cty Fidutech - MB
- Bước 2: Nhắn tin tới Zalo Fidutech - nhấn vào đây để thông báo và nhận tài liệu
Xem toàn bộ: Giáo án điện tử chuyên đề toán 12 cánh diều
ĐẦY ĐỦ GIÁO ÁN CÁC BỘ SÁCH KHÁC
GIÁO ÁN WORD LỚP 12 CÁNH DIỀU
Giáo án hoạt động trải nghiệm hướng nghiệp 12 cánh diều
Giáo án Tin học 12 - Định hướng khoa học máy tính cánh diều
Giáo án Tin học 12 - Định hướng Tin học ứng dụng cánh diều
GIÁO ÁN POWERPOINT LỚP 12 CÁNH DIỀU
Giáo án Powerpoint Toán 12 Cánh diều
Giáo án powerpoint hình học 12 cánh diều
Giáo án powerpoint đại số 12 cánh diều
Giáo án powerpoint vật lí 12 cánh diều
Giáo án powerpoint sinh học 12 cánh diều
Giáo án powerpoint hoá học 12 cánh diều
Giáo án powerpoint ngữ văn 12 cánh diều
Giáo án powerpoint lịch sử 12 cánh diều
Giáo án powerpoint địa lí 12 cánh diều
Giáo án powerpoint Kinh tế pháp luật 12 cánh diều
Giáo án powerpoint Công nghệ 12 Công nghệ điện - điện tử cánh diều
Giáo án powerpoint Công nghệ 12 Lâm nghiệp - Thuỷ sản cánh diều
Giáo án powerpoint Tin học 12 - Định hướng Tin học ứng dụng cánh diều
Giáo án powerpoint Tin học 12 - Định hướng khoa học máy tính cánh diều
Giáo án powerpoint hoạt động trải nghiệm hướng nghiệp 12 cánh diều
GIÁO ÁN CHUYÊN ĐỀ LỚP 12 CÁNH DIỀU
GIÁO ÁN POWERPOINT CHUYÊN ĐỀ 12 CÁNH DIỀU
GIÁO ÁN DẠY THÊM LỚP 12 CÁNH DIỀU
Giáo án dạy thêm toán 12 cánh diều
Giáo án dạy thêm ngữ văn 12 cánh diều
Giáo án powerpoint dạy thêm ngữ văn 12 cánh diều
Giáo án powerpoint dạy thêm toán 12 cánh diều
