Trắc nghiệm câu trả lời ngắn Toán 12 chân trời Bài 3: Ứng dụng hình học của tích phân

BÀI 3. ỨNG DỤNG HÌNH HỌC CỦA TÍCH PHÂN

Câu 1: Thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường ;

; quay quanh trục bằng , tối giản). Tính

bằng bao nhiêu?

• 13

Câu 2: Một vật chuyển động với gia tốc được cho bởi hàm số .Lúc bắt đầu chuyển động vật có vận tốc . Gia tốc của vật tại thời điểm vận tốc đạt giá trị lớn nhất trong (s) đầu tiên là bao nhiêu m/s?

• 25

Câu 3: Một xe mô tô phân khối lớn sau khi chờ hết đèn đỏ đã bắt đầu phóng nhanh với vận tốc tăng liên tục được biểu thị bằng đồ thị là đường Parabol như hình vẽ. Biết rằng sau thì xe đạt đến vận tốc cao nhất và bắt đầu giảm tốc. Hỏi từ lúc bắt đầu đến lúc đạt vận tốc cao nhất thì xe đã đi được quãng đường bao nhiêu mét?

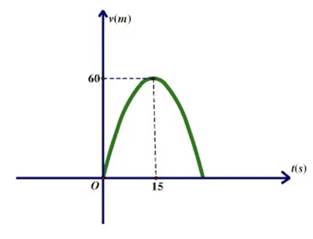
• 600

Câu 4: Một thùng đựng Bia hơi (có dạng như hình vẽ) có đường kính đáy là 30cm, đường kính lớnnhất của thân thùng là 40cm, chiều cao thùng là 60 cm, cạnh bên hông của thùng có hình dạng của một parabol. Thể tích của thùng Bia hơi là bao nhiêu lít? (làm tròn đến hàng phần chục).

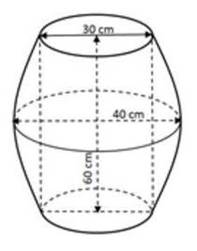
• 63,8

Câu 5: Cho hình vuông có cạnh bằng được chia thành hai phần bởi đường cong có phương trình . Gọi lần lượt là diện tích của phần không bị gạch và bị gạch như hình vẽ bên dưới. Tính tỉ số .

• 2

Câu 6: Cho là hình phẳng giới hạn bởi đồ thị hàm số , trục hoành và trục tung. Biết đường thẳng đi qua và chia thành hai phần có diện tích bằng nhau (Hình vẽ). Giá trị bằng

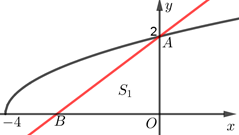
• 2

BÀI TẬP THAM KHẢO THÊM

Câu hỏi 1: Cho hình phẳng (H) giới hạn bởi các đường y = cos x; y = 0; x = 0 và x = π/2 . Tính thể tích vật thể tròn xoay có được khi (H) quay quanh trục Ox.

Trả lời:

Câu hỏi 2: Cho hàm số y = f(x) liên tục trên đoạn [a; b]. Tính diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số y = f(x), trục hoành và hai đường thẳng x = a, x = b, (a < b).

Trả lời: S = dx

Câu hỏi 3: Cho hình phẳng (H) giới hạn bởi các đường y = 2x − x² , y = 0. Tính thể tích khi quay (H) quanh trục hoành tạo thành khối tròn xoay 

Trả lời: dx 

Câu hỏi 4: Gọi (D) là hình phẳng giới hạn bởi các đường y = , y = 0, x = 1, x = 4. Tính thể tích vật thể tròn xoay tạo thành khi quay hình (D) quanh trục Ox.

Trả lời:

Câu hỏi 5: Cho hàm số y = f(x) liên tục trên R và có đồ thị (C) là đường cong như hình bên. Diện tích hình phẳng giới hạn bởi đồ thị (C), trục hoành và hai đường thẳng x = 0 , x = 2 (phần tô tím). Tính diện tích phần tô tím

Trả lời: dx - dx

Câu hỏi 6: Diện tích hình phẳng bôi đậm trong hình vẽ dưới đây được xác định theo công thức:

Trả lời: ......................................

Câu hỏi 7: Cho hàm số y = f ( x ) liên tục trên [ a ; b ] , a < b . Tính diện tích hình phẳng ( H ) giới hạn bởi đồ thị hàm số f ( x ), trục hoành và hai đường thẳng x = a ; x = b 

Trả lời: ......................................

Câu hỏi 8: Viết công thức tính thể tích V của phần vật thể bị giới hạn bởi hai mặt phẳng vuông góc với trục Ox tại các điểm x = a , x = b ( a < b), có diện tích thiết diện cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x ( a ≤ x ≤ b) là S ( x )

Trả lời: ......................................

Câu hỏi 9: Cho hình phẳng D giới hạn bởi đường cong y = e ^x , trục hoành và các đường thẳng x = 0, x = 1. Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng bao nhiêu?

Trả lời: ......................................

Câu hỏi 10: Cho đồ thị hàm số y = f(x). Tính diện tích hình phẳng (phần tô đậm trong hình)

Trả lời: ......................................

Câu hỏi 11: Cho parabol (P) có đồ thị hình vẽ:

Tính diện tích hình phẳng giới hạn bởi (P) với trục hoành.

Trả lời: ......................................

Câu hỏi 12: Kí hiệu S là diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x), trục hoành, đường thẳng x = a, x = b (như hình bên). Tính S

Trả lời: ......................................

Câu hỏi 13: Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số , trục hoành và hai đường thẳng x = 1; x = 2. Gọi V là thể tích của khối tròn xoay thu được khi quay hình (H) xung quanh trục hoành. Tính V

Trả lời: ......................................

Câu hỏi 14: Cho hình phẳng (H) như hình vẽ. Tính diện tích hình phẳng (H)

Trả lời: ......................................

Câu hỏi 15: Diện tích hình phẳng giới hạn bởi hàm số , trục Ox và đường thẳng x =1 bằng với a , b , c là các số nguyên dương. Tính giá trị của a + b + c 

Trả lời: ......................................

Câu hỏi 16: Cho hình phẳng giới hạn bởi các đường y = x², y = 0, x = 0, x = 4. Đường thẳng y = k (0 < k < 16) chia hình (H) thành hai phần có diện tích S₁, S₂ (hình vẽ)

Trả lời: ......................................

Câu hỏi 17: Tính diện tích của hình phẳng (H) được giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng x = a, x = b (a < b) (phần tô đậm trong hình vẽ)

Trả lời: ......................................

Câu hỏi 18: Cho hàm số y = (với m là tham số khác 0) có đồ thị là (C). Gọi S là diện tích hình phẳng giới hạn bởi đồ thị (C) và hai trục tọa độ. Có bao nhiêu giá m trị thực của thỏa mãn S = 1?

Trả lời: ......................................

Câu hỏi 19: Cho hàm số có đồ thị y = x4 – 4x2 +m. Giả sử (Cm) cắt trục hoành tại bốn điểm phân biệt sao cho diện tích hình phẳng giới hạn bởi (CM)với trục hoành có diện tích phần phía trên trục hoành bằng diện tích phần phía dưới trục hoành. Tìm m?

Trả lời: ......................................

Câu hỏi 20: Trong không gian Oxyz, cho vật thể được giới hạn bởi hai mặt phẳng ( P ) , ( Q ) vuông góc với trục Ox lần lượt tại x = a , x = b ( a < b ). Một mặt phẳng ( R ) tùy ý vuông góc với Ox tại điểm có hoành độ x , ( a ≤ x ≤ b ) cắt vật thể theo thiết diện có diện tích là S ( x ), với y = S ( x ) là hàm số liên tục trên [ a ; b ]. Thể tích V của vật thể đó được tính theo công thức

Trả lời: ......................................

----------------------------------

----------------------- Còn tiếp -------------------------