Giáo án điện tử bài 2 - Số thực. Giá trị tuyệt đối của một số thực

CHÀO MỪNG CÁC EM ĐẾN VỚI TIẾT HỌC HÔM NAY!

KHỞI ĐỘNG

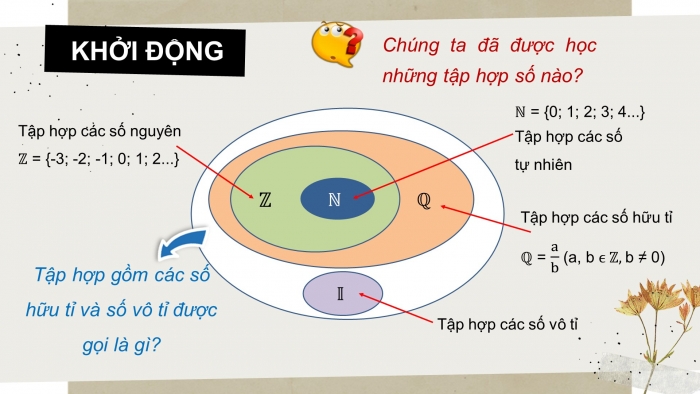
Tập hợp gồm các số hữu tỉ và số vô tỉ được gọi là gì?

Tập hợp các số nguyên

 = {-3; -2; -1; 0; 1; 2...}

 = {0; 1; 2; 3; 4...}

Tập hợp các số

tự nhiên

Tập hợp các số hữu tỉ

 =  (a, b b ≠ 0)

BÀI 2: SỐ THỰC. GIÁ TRỊ TUYỆT ĐỐI CỦA MỘT SỐ THỰC (4 Tiết)

NỘI DUNG BÀI HỌC

1. Số thực và tập hợp các số thực
2. Thứ tự trong tập hợp các số thực
3. Trục số thực
4. Số đối của một số thực
5. Giá trị tuyệt đối của một số thực
6. Số thực và tập hợp các số thực

HĐKP1: Trong các số sau, số nào là số hữu tỉ, số nào là số vô tỉ?

;       3,(45);     ;        -45;        -  ;       0;

Các số:   ; 3,(45) ; -45 ; 0 là số hữu tỉ

Các số  ; -  ;  π là số vô tỉ.

KẾT LUẬN

• Ta gọi chung số hữu tỉ và số vô tỉ là số thực.
• Tập hợp các số thực được kí hiệu là .
• Các em đã biết những loại số thập phân nào?

Ghi nhớ

Mỗi số thực chỉ có một trong hai dạng biểu diễn thập phân sau đây:

• Dạng thập phân hữu hạn hay vô hạn tuần hoàn nếu đó là số hữu tỉ.
• Dạng thập phân vô hạn không tuần hoàn nếu số đó là số vô tỉ.

Ví dụ 1:

Thực hành 1:

Các khẳng định sau đây đúng hay sai? Nếu sai, hãy phát biểu lại cho đúng.

1. a) ;         b)                c)                 d) -9    

Chú ý:

KẾT LUẬN:

Trong tập hợp các số thực, ta cũng có các phép  tính với các tính chất tương tự như các phép tính trong tập hợp các số hữu tỉ mà ta đã biết.

2. Thứ tự trong tập hợp các số thực

Hoạt động nhóm đôi và hoàn thành HĐKP2

HĐKP2

Hãy so sánh các số thập phân sau đây: 3,14;  3,1415;  3,141515

3,14 < 3,1415 < 3,141515

Các số thập phân hữu hạn hoặc vô hạn đều có thể được so sánh tương tự như so sánh hai số thập phân hữu hạn.

Kết luận:

Với hai số thực x, y bất kì, ta luôn có hoặc x < y hoặc x > y hoặc x = y.

Ví dụ 2

1,4527...< 1,45(31);  = 1,73205... < 1,733; -3,52681... > -3,52693...

Chú ý: Với hai số thực dương a và b, ta có: Nếu a > b thì

Ví dụ 3: Do 3 > 2 nên  >

Thực hành 2: So sánh hai số thực

1. 4,(56) và 4,56279 b) -3,(65) và -3,6491
2. c) 0,(21) và 0,2(12) d) và 1,42

Giải

1. a) Có: 4,(56) = 4,5656….

Vì 4,5656… > 4,56279, do đó 4,(56) > 4,56279

1. b) Có: -3,(65) = -3,6565…

Vì -3,6565…< -3,6491, do đó -3,(65) < -3,6491

2121. c) Có: 0,(21) = 0,2121...= = ; 0,2(12) = 0,21212... = =  

Do đó 0,(21) = 0,2(12)

1. d) Có: = 1,4142…

Vì 1,4142…< 1,42, do đó  < 1,42

Vận dụng 1

Cho một hình vuông có diện tích 5 m². Hãy so sánh độ dài a của cạnh hình vuông đó với độ dài b = 2,361 m.

Cho một hình vuông có diện tích 5 m². Hãy so sánh độ dài a của cạnh hình vuông đó với độ dài b = 2,361 m.

3. Trục số thực

HĐKP3

Quan sát hình vẽ bên và cho biết độ dài của đoạn thẳng OA bằng bao nhiêu.

Độ dài OA có là số hữu tỉ hay không?

Đường chéo OA của hình vuông có độ dài là 1 bằng  là số vô tỉ.

Ta có thể biểu diễn số vô tỉ  trên trục số như sau:

Không phải mỗi điểm trên trục số đều biểu diễn một số hữu tỉ (hay các điểm biểu diễn số hữu tỉ không lấp đầy trục số).

Kết luận:

• Mỗi số thực được biểu diễn bởi một điểm trên trục số.
• Ngược lại, mỗi điểm trên trục số biểu diễn một số thực.

Chú ý

• Điểm biểu diễn số thực x trên trục số được gọi là điểm x.
• Nếu x < y thì trên trục số nằm ngang, điểm x ở bên trái điểm y.

Thực hành 3

Hãy biểu diễn các số thực -2; -  ; -1,5; 2; 3 trên trục số.

Vận dụng 2

Không cần vẽ hình, hãy nêu nhận xét về vị trí của hai số ;  trên trục số.

 = 1,5 ;  = 1,4142..

Có:  = 1,4142.. <  = 1,5   nằm bên trái số .

4. Số đối của một số thực

Thảo luận cặp đôi, thực hiện HĐKP4

HĐKP4

Gọi A và A’ lần lượt là các điểm biểu diễn của hai số 4,5 và -4,5 trên trục số. So sánh OA và OA’.

                 Có: OA = 4,5 và OA’= 4,5

 ⇒ OA = OA’.

Kết luận

• Hai số thực có điểm biểu diễn trên trục số cách đều điểm gốc O và nằm về hai phía ngược nhau là hai số đối nhau, số này gọi là số đối của số kia.
• Số đối của số thực x kí hiệu là – x. Ta có x + (-x) = 0.

Ví dụ 5: Số đối của  là ; số đối của  là . 

Thực hành 4

Tìm số đối của các số thực sau: 5,12; ; -

Số đối của các số thực  5,12 ; π ;  

lần lượt là: -5,12 ; -π ;

Vận dụng 3

So sánh các số đối của hai số  và

Các số đối của hai số  và   lần lượt là:  và  .

Do 2 < 3 =>  <  =>  >  .

5. Giá trị tuyệt đối của một số thực

Thảo luận nhóm đôi trả lời câu hỏi HĐKP5.

HĐKP5

Khoảng cách từ O đến hai điểm   và  bằng nhau.

KẾT LUẬN:

• Giá trị tuyệt đối của một số thực x là khoảng cách từ điểm x đến điểm 0 trên trục số.
• Giá trị tuyệt đối của một số thực x được kí hiệu là |x|.

Nhận xét:

Giá trị tuyệt đối của một số thực x luôn là số không âm:  với mọi số thực x.

Ví dụ 6

|-3| = 3;         |-  | =  ;      |0,345| = 0,345;   

| | = ;     |-  | =  ;    |- | =     

Thực hành 5

Tìm giá trị tuyệt đối của các số thực sau: -3,14; 41; -5; 1,(2); -

|-3,14| = 3,14      |41| = 41      |-5| = 5             |1,(2)| = 1,(2)               |- | =

Vận dụng 4

                 Có bao nhiêu số thực x thỏa mãn |x| = ?

Giải:

     hoặc  

LUYỆN TẬP

Bài 1 (SGK - tr38): Thay mỗi dấu ? bằng kí hiệu  hoặc  để có phát biểu đúng.

Bài 2 (SGK - tr38)

Sắp xếp các số thực sau theo thứ tự từ nhỏ đến lớn: ; 4,1; - ; 3,2; ; - ;

 = - 0,(6);    = 1,4142..;    = 3,1415..;       = -0,75;     = 2,(3).

Vì -1,4142...< -0,75 < -0,(6) < 2,(3) < 3,1415...< 3,2 < 4,1

 <  <  <  < π < 3,2 < 4,1

Vậy thứ tự từ nhỏ đến lớn là:  ;  ;  ;  ; π ; 3,2 ; 4,1.

Bài 6 (SGK - tr38)

Tìm giá trị tuyệt đối của các số sau: - ;   52,(1);   0,68;  - ;   2

|- | = ;    |52,(1)| = 52,1 ;   |0,68| = 0,68;    | | = ;     |2 | = 2

Bài 8 (SGK - tr38)

Tìm giá trị của x và y biết rằng: |x| = ; |y - 2| = 0

Giải

 hoặc 

VẬN DỤNG

Câu 1: Phát biểu sau đây là sai?

1. Mọi số thực đều là số vô tỉ
2. Mọi số vô tỉ đều là số thực
3. Mọi số nguyên là số hữu tỉ
4. Số 0 là số hữu tỉ cũng là số thực

Câu 2: Phát biểu nào sau đây là đúng?

1. Số nguyên không phải số thực
2. Phân số không phải số thực
3. Số vô tỉ không phải số thực
4. Cả ba loại số trên đều là số thực

Câu 3: Chọn chữ số thích hợp điền vào chỗ trống

-11,29 < -11,...9

1. 1; 2; 3; ...9
2. 3
4. 0; 1

Câu 4: Chọn khẳng định sai trong các khẳng định sau

1. ; ; là các số thực.
2. ; ; -0,45 là các số thực.
3. Số 0 vừa là số hữu tỉ, vừa là số vô tỉ.
4. 1; 2; 3; 4 là các số thực.

Câu 5: Sắp xếp từ nhỏ đến lớn giá trị tuyệt đối của các số -3,2 ; 2,13;  ;  

1. ; ; ;
2. ;  ; ;
3. ; ; ;
4. ; ; ;

Câu 6: Số đối của các số ; 12,(3); 0,4599 ;  ; -π lần lượt là:

1. ; 12,(3); 0,4599;  ; π
2. ; 12,(3) ; 0,4599 ;  ; -π
3. ; -12,(3); -0,4599;  ; -π
4. ; -12,(3); -0,4599;  ; π

HƯỚNG DẪN VỀ NHÀ

Ghi nhớ kiến thức đã học trong bài.

Hoàn thành các bài tập còn lại trong SGK và làm bài tập SBT.

Chuẩn bị bài mới “Bài 3. Làm tròn số và ước lượng kết quả”

CẢM ƠN CÁC EM ĐÃ LẮNG NGHE BÀI GIẢNG!