Giáo án điện tử toán 7 chân trời bài 6: Tính chất ba đường trung trực của tam giác
Bài giảng điện tử toán 7 chân trời. Giáo án powerpoint bài 6: Tính chất ba đường trung trực của tam giác. Giáo án thiết kế theo phong cách hiện đại, nội dung đầy đủ, đẹp mắt tạo hứng thú học tập cho học sinh. Thầy cô giáo có thể tham khảo.
Xem: => Giáo án toán 7 chân trời sáng tạo (bản word)
Các tài liệu bổ trợ khác
Xem toàn bộ: Giáo án điện tử toán 7 chân trời sáng tạo
CHÀO MỪNG CÁC EM ĐẾN VỚI BÀI HỌC MỚI
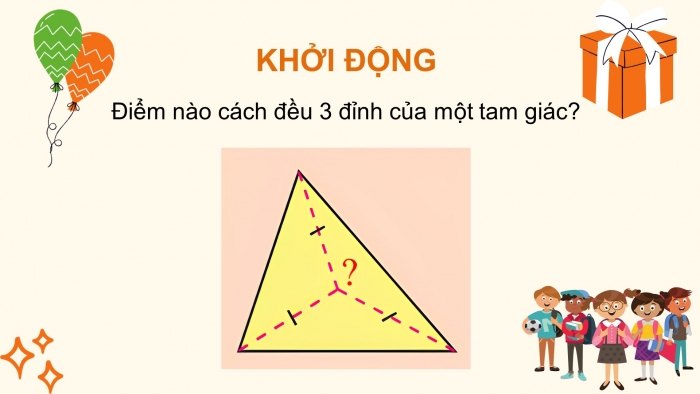
KHỞI ĐỘNG
Điểm nào cách đều 3 đỉnh của một tam giác?
BÀI 6: TÍNH CHẤT BA ĐƯỜNG TRUNG TRỰC CỦA TAM GIÁC
NỘI DUNG BÀI HỌC
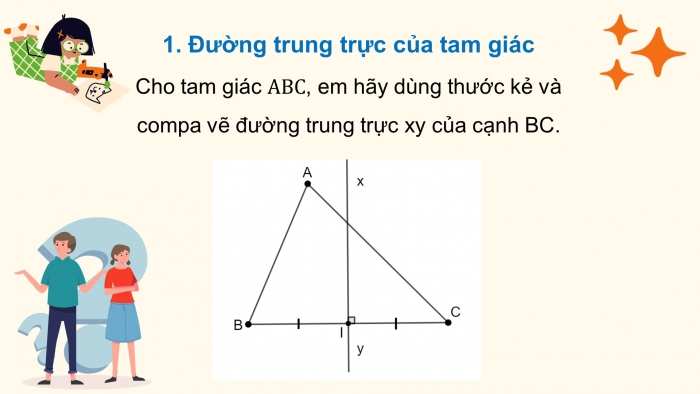
Đường trung trực của tam giác
Tính chất ba đường trung trực của tam giác
- Đường trung trực của tam giác
Cho tam giác , em hãy dùng thước kẻ và compa vẽ đường trung trực xy của cạnh BC.
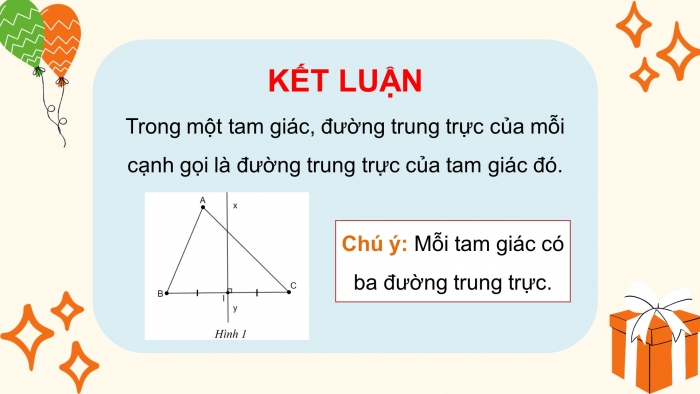
KẾT LUẬN
Trong một tam giác, đường trung trực của mỗi cạnh gọi là đường trung trực của tam giác đó.
Chú ý: Mỗi tam giác có ba đường trung trực.
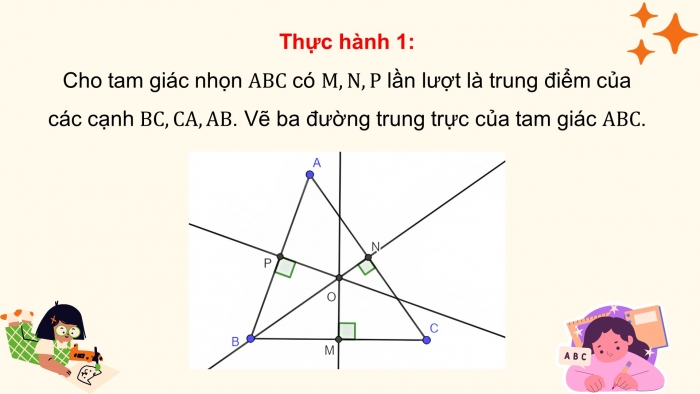
Thực hành 1:
Cho tam giác nhọn có lần lượt là trung điểm của các cạnh . Vẽ ba đường trung trực của tam giác .
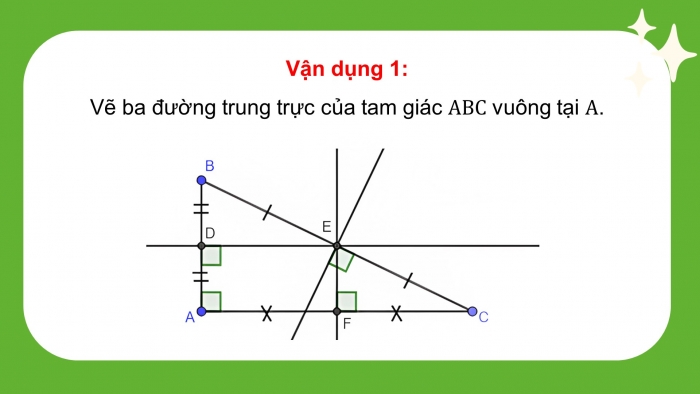
Vận dụng 1:
Vẽ ba đường trung trực của tam giác vuông tại .
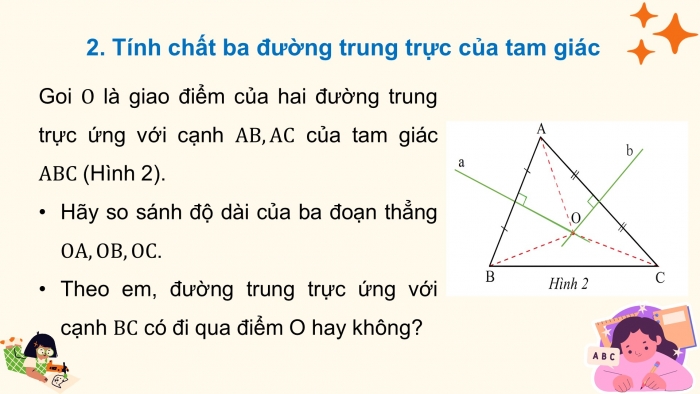
- Tính chất ba đường trung trực của tam giác
Goi là giao điểm của hai đường trung trực ứng với cạnh của tam giác (Hình 2).
- Hãy so sánh độ dài của ba đoạn thẳng .
- Theo em, đường trung trực ứng với cạnh có đi qua điểm O hay không?
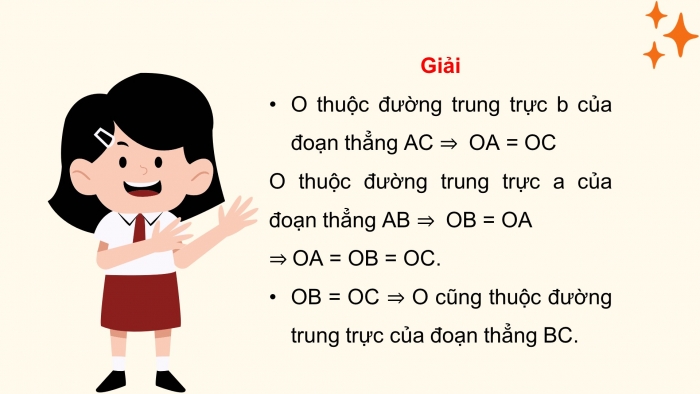
Giải
- O thuộc đường trung trực b của đoạn thẳng AC OA = OC
O thuộc đường trung trực a của đoạn thẳng AB OB = OA
OA = OB = OC.
- OB = OC O cũng thuộc đường trung trực của đoạn thẳng BC.
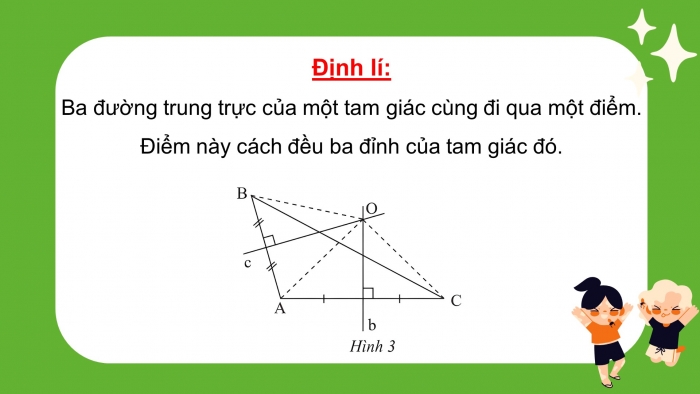
- Định lí:
- Ba đường trung trực của một tam giác cùng đi qua một điểm. Điểm này cách đều ba đỉnh của tam giác đó.
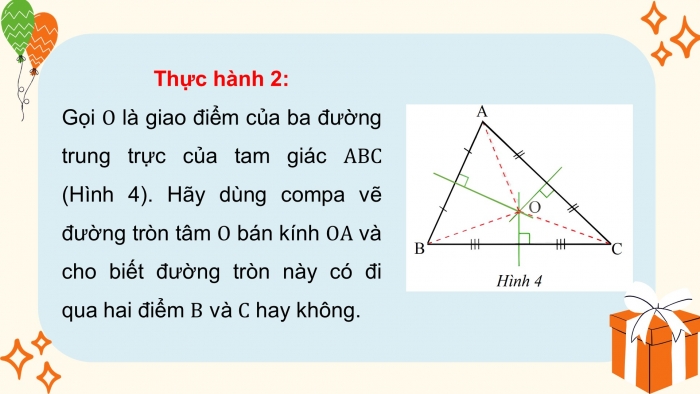
- Thực hành 2:
- Gọi là giao điểm của ba đường trung trực của tam giác (Hình 4). Hãy dùng compa vẽ đường tròn tâm bán kính và cho biết đường tròn này có đi qua hai điểm và hay không.
- Giải
- O là giao điểm của ba đường trung trực trong tam giác ABC
- OA = OB = OC
- OB, OC cũng là bán kính đường tròn tâm O.
- B, C thuộc đường tròn tâm O bán kính OA.
- Vận dụng 2:
- Trên bản đồ quy hoạch một khu dân cư có ba điểm dân cư (Hình 5). Tìm địa điểm để xây một trường học sao cho trường học này cách đều ba điểm đân cư đó.
Giải
M cách đều A và B
M thuộc đường trung trực của AB.
M cách đều A và C
M thuộc đường trung trực của AC.
M cách đều C và B
M thuộc đường trung trực của BC.
M là giao của ba đường trung trực trong tam giác ABC.
Câu 1. Gọi O là giao điểm của ba đường trung trực trong . Khi đó O là:
- Điểm cách đều ba cạnh của
- Điểm cách đều ba đỉnh của
- Điểm nằm trên đường trung trực của đoạn thẳng BC.
- Đáp án B và C đúng
Câu 2. Cho tam giác ABC cân tại A có d là đường trung trực của cạnh AB và AE là tia phân giác của góc BAC ( , O là giao điểm của d và AE. Khi đó điểm O là:
- Điểm nằm trên đường trung trực của cạnh AC.
- Trung điểm của AE.
- Điểm cách đều ba cạnh của tam giác ABC.
Câu 3. Cho tam giác đều ABC và điểm G như trong Hình 8. Hãy chọn khẳng định sai.
- GA = GB = GC
- G cách đều ba đỉnh của tam giác ABC.
- C thuộc đường trung trực của AB.
Trên chỉ là 1 phần của giáo án. Giáo án khi tải về có đầy đủ nội dung của bài. Đủ nội dung của học kì I + học kì II
Hệ thống có đầy đủ các tài liệu:
- Giáo án word (300k)
- Giáo án Powerpoint (350k)
- Trắc nghiệm theo cấu trúc mới (150k)
- Đề thi cấu trúc mới: ma trận, đáp án, thang điểm..(200k)
- Phiếu trắc nghiệm câu trả lời ngắn (150k)
- Trắc nghiệm đúng sai (150k)
- Lý thuyết bài học và kiến thức trọng tâm (150k)
- File word giải bài tập sgk (150k)
- Phiếu bài tập để học sinh luyện kiến thức (150k)
- .....
Nâng cấp lên VIP đê tải tất cả ở tài liệu trên
- Phí nâng cấp VIP: 900k
=> Chỉ gửi 500k. Tải về dùng thực tế. Nếu hài lòng, 1 ngày sau mới gửi phí còn lại
Cách tải hoặc nâng cấp:
- Bước 1: Chuyển phí vào STK: 1214136868686 - cty Fidutech - MB(QR)
- Bước 2: Nhắn tin tới Zalo Fidutech - nhấn vào đây để thông báo và nhận tài liệu
Xem toàn bộ: Giáo án điện tử toán 7 chân trời sáng tạo
GIÁO ÁN WORD LỚP 7 - SÁCH CHÂN TRỜI
GIÁO ÁN POWERPOINT LỚP 7 - SÁCH CHÂN TRỜI
GIÁO ÁN LỚP 7 CÁC BỘ SÁCH KHÁC
Giáo án đủ các môn lớp 7 sách kết nối tri thức (bản word)
Giáo án đủ các môn lớp 7 sách kết nối tri thức (bản powrerpoint)
Giáo án đủ các môn lớp 7 sách cánh diều (bản word)
Giáo án đủ các môn lớp 7 sách cánh diều (bản powrerpoint)