Giáo án điện tử Toán 11 cánh diều Chương 4 Bài 3: Đường thẳng và mặt phẳng song song

CHÀO MỪNG CÁC EM ĐẾN VỚI BUỔI HỌC HÔM NAY!

KHỞI ĐỘNG

Trong thực tiễn, ta thường gặp nhiều đồ dùng, vật thể gợi nên hình ảnh đường thẳng song song với mặt phẳng. Chẳng hạn, thanh barrier song song với mặt phẳng (Hình 44).

Thế nào là đường thẳng song song với mặt phẳng trong không gian?

BÀI 3. ĐƯỜNG THẲNG VÀ MẶT PHẲNG SONG SONG

NỘI DUNG BÀI HỌC

Đường thẳng song song với mặt phẳng

Điều kiện và tính chất

1. ĐƯỜNG THẲNG SONG SONG VỚI MẶT PHẲNG

Thảo luận nhóm đôi

HĐ1

1. a) Trong Hình 44, thanh barrier và mặt phẳng gợi nên hình ảnh đường thẳng d và mặt phẳng (P). Cho biết đường thẳng d và mặt phẳng (P) có điểm chung hay không.
2. b) Cho đường thẳng d và mặt phẳng (P). Hãy cho biết các khả năng có thể xảy ra đối với số điểm chung của d và (P).

Giải

1. a) Trong Hình 44 đường thẳng d và mặt phẳng (P) không có điểm chung.
2. b) Các khả năng xảy ra với số điểm chung của d và (P) là:

• Vô số điểm chung
• 1 điểm chung
• Không có điểm chung.

Nhận xét

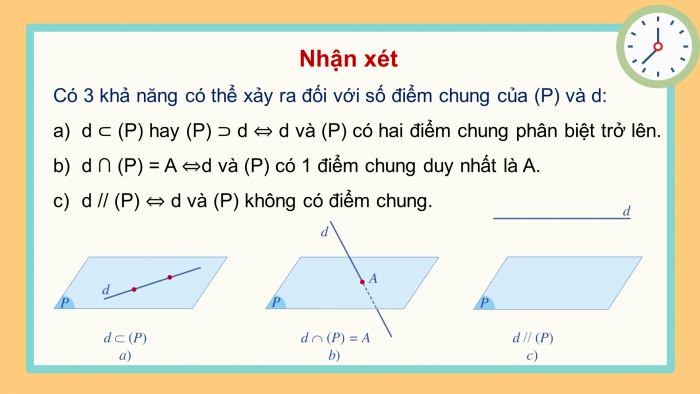
Có 3 khả năng có thể xảy ra đối với số điểm chung của (P) và d:

1. d ⊂ (P) hay (P) ⊃ d ⇔ d và (P) có hai điểm chung phân biệt trở lên.
2. d ∩ (P) = A ⇔d và (P) có 1 điểm chung duy nhất là A.
3. d // (P) ⇔ d và (P) không có điểm chung.

KẾT LUẬN

Đường thẳng a song song với mặt phẳng (P) nếu chúng không có điểm chung.

Ví dụ 1

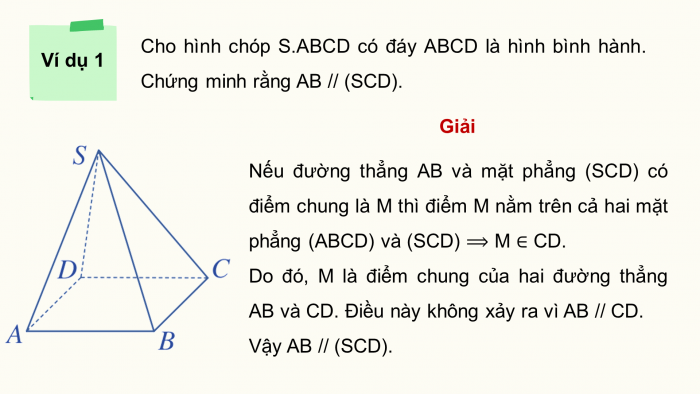
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Chứng minh rằng AB // (SCD).

Giải

Nếu đường thẳng AB và mặt phẳng (SCD) có điểm chung là M thì điểm M nằm trên cả hai mặt phẳng (ABCD) và (SCD)  M  CD.

Do đó, M là điểm chung của hai đường thẳng AB và CD. Điều này không xảy ra vì AB // CD.

Vậy AB // (SCD).

Luyện tập 1

Quan sát các xà ngang trên sân tập thể dục ở Hình 47. Hãy cho biết vị trí tương đối của các xà ngang đó với mặt sân.

Giải

Xà ngang song song với mặt sân

1. ĐIỀU KIỆN VÀ TÍNH CHẤT

Thảo luận nhóm đôi

HĐ2

Cho đường thẳng a không nằm trong mặt phẳng (P) và a song song với đường thẳng a’ nằm trong (P) (Hình 48). Gọi (Q) là mặt phẳng xác định bởi hai đường thẳng song song a, a’.

1. a) Giả sử a cắt (P) tại M. Đường thẳng a có cắt đường thẳng a’ tại M hay không?
2. b) Nêu vị trí tương đối của đường thẳng a và mặt phẳng (P). Vì sao?

Giải

1. a) Do a’ ⊂ (P) và a’ ⊂ (Q) nên (P) ∩ (Q) = a’.

Mà a cắt (P) tại M nên M ∈ (P)

Lại có M ∈ a, a ⊂ (Q) nên M ∈ (Q)

Suy ra M là giao điểm của (P) và (Q).

Do đó giao tuyến a’ của hai mặt phẳng đi qua điểm M.

Vậy đường thẳng a cắt đường thẳng a’ tại M.

1. b) Theo câu a, nếu a cắt (P) tại M thì đường thẳng a và đường thẳng a’ cắt nhau tại M.

Điều này là mâu thuẫn với giả thiết là hai đường thẳng a và a’ song song.

Do đó a không có điểm chung với (P) nên a // (P).

ĐỊNH LÍ 1 (Dấu hiệu nhận biết một đường thẳng song song với một mặt phẳng):

Nếu đường thẳng a không nằm trong mặt phẳng (P) và song song với một đường thẳng nằm trong (P) thì a song song với (P).

Sử dụng định lí để chứng minh đường thẳng song song với mặt phẳng, ta chỉ cần chỉ ra điều gì?

a // a’

a ⊄ (P)

a' ⊂ (P)

 a // (P)

Sử dụng Định lí để trình bày Ví dụ 2 (SGK - tr.102)

Ví dụ 2

Cho hình chóp S.ABCD. Gọi M, N lần lượt là trung điểm của các cạnh SA, SC. Chứng minh rằng đường thẳng MN song song với mặt phẳng (ABCD).

Giải

Vì M, N lần lượt là trung điểm của các cạnh SA, SC nên MN là đường trung bình của SAC

 MN // AC mà AC  (ABCD)

 MN // (ABCD) (theo Định lí 1)

                             Cho tứ diện ABCD. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AC, AD. Các đường thẳng MN, NP, PM có song song với mặt phẳng (BCD) không? Vì sao?

Giải

Xét ∆ABC có M, N lần lượt là trung điểm của AB, AC nên MN là đường trung bình của tam giác  MN // BC.

Lại có BC ⊂ (BCD), MN ⊄ (BCD) MN // (BCD).

Chứng minh tương tự: NP // CD, CD ⊂ (BCD)

 NP // (BCD).

Tương tự, MP // BD mà BD ⊂ (BCD) MP // (BCD).

Thực hiện nhóm đôi

HĐ3

Cho đường thẳng a song song với mặt phẳng (P). Cho mặt phẳng (Q) chứa a và cắt (P) theo giao tuyến b. (Hình 51).

1. Giả sử a cắt b tại M. Đường thẳng a có cắt mặt phẳng (P) tại M hay không?
2. Nêu vị trí tương đối của hai đường thẳng a và b. Vì sao?

Giải

1. a) Ta có a ∩ b = {M} nên M ∈ b

Mà b ⊂ (P), do đó M ∈ (P).

Lại có M ∈ a.

Vậy đường thẳng a cắt mặt phẳng (P) tại M.

1. b) Theo câu a, nếu a cắt b tại M thì a cắt (P) tại M, điều này mâu thuẫn với giả thiết đường thẳng a song song với mặt phẳng (P).

Do đó a và b không cắt nhau và cùng nằm trong mặt phẳng (Q)  a // b.

Vậy hai đường thẳng a và b song song với nhau.

ĐỊNH LÍ 2 (Tính chất của đường thẳng song song với mặt phẳng)