Giáo án và PPT Toán 10 cánh diều Bài 2: Hệ bất phương trình bậc nhất hai ẩn
Đồng bộ giáo án word và powerpoint (ppt) Bài 2: Hệ bất phương trình bậc nhất hai ẩn. Thuộc chương trình Toán 10 cánh diều. Giáo án được biên soạn chỉn chu, hấp dẫn. Nhằm tạo sự lôi cuốn và hứng thú học tập cho học sinh.
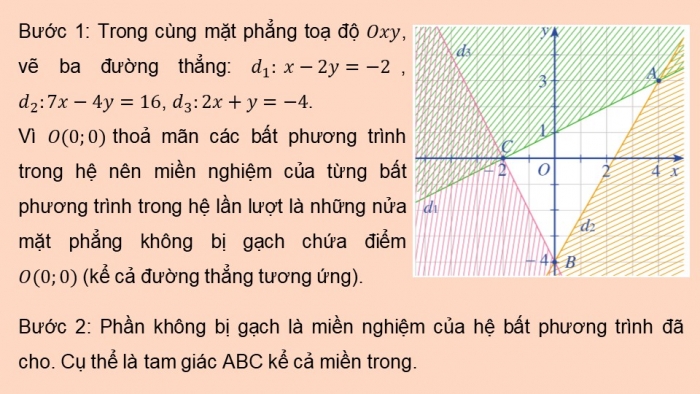
Click vào ảnh dưới đây để xem giáo án WORD rõ nét












Giáo án ppt đồng bộ với word











Còn nữa....
Các tài liệu bổ trợ khác
Xem toàn bộ: Trọn bộ giáo án và PPT Toán 10 cánh diều
CHƯƠNG II. BẤT PHƯƠNG TRÌNH VÀ HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN.
BÀI 2. HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
HOẠT ĐỘNG KHỞI ĐỘNG
GV yêu cầu HS thảo luận và trả lời:
Trong năm nay, một cửa hàng điện lạnh dự định kinh doanh hai loại máy điều hoà điều hoà hai chiều và điều hoà một chiều với số vốn ban đầu không vượt quá 1,2 tỷ đồng.
| Điều hòa hai chiều | Điều hòa một chiều | |
| Giá mua vào | 20 triệu đồng/1 máy | 10 triệu đồng/1 máy |
| Lợi nhuận dự kiến | 3,5 triệu đồng/1 máy | 2 triệu đồng/1 máy |
Cửa hàng ước tính rằng tổng nhu cầu của thị trường sẽ không vượt quá 100 máy cả hai loại. Nếu là chủ cửa hàng thì em cần đầu tư kinh doanh mỗi loại bao nhiêu máy đề lợi nhuận thu được là lớn nhất?
HOẠT ĐỘNG HÌNH THÀNH KIẾN THỨC
HOẠT ĐỘNG 1. HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
GV đặt câu hỏi hướng dẫn học sinh tìm hiểu: Trong tình huống mở đầu, gọi x và y lần lượt là số máy điều hoà loại hai chiều và một chiều mà cửa hàng cần nhập. Tính số tiền vốn mà cửa hàng phải bỏ ra để nhập hai loại máy điều hoà theo x và y.
a) Do nhu cầu của thị trường không quá 100 máy nên x và y cần thoả mãn điều kiện gì?
b) Vì số vốn mà chủ cửa hàng có thể đầu tư không vượt quá 1,2 tỉ đồng nên x và y phải
thoả mãn điều kiện gì?
c) Tính số tiền lãi mà cửa hàng dự kiến thu được theo x và y.
Sản phẩm dự kiến:
Số tiền vốn mà cửa hàng phải bỏ ra để mua hai loại máy điều hòa là:
20x + 10y (triệu đồng).
a) ![]()
b) ![]()
c) ![]() .
.
HOẠT ĐỘNG 2. BIỂU DIỄN MIỀN NGHIỆM CỦA HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN.
HS cùng thảo luận và trả lời câu hỏi: Cho đường thẳng d: x+y=150 trên mặt phẳng tọa độ Oxy. Đường thẳng này cắt hai trục tọa độ Ox và Oy tại hai điểm A và B.
a) Xác định miền nghiệm D1,D2,D3D1,D2,D3 của các bất phương trình tương ứng x≥0;y≥0x≥0;y≥0 và x+y≤150x+y≤150.
b) Miền tam giác OAB (H.2.5) có phải là giao điểm của các miền D1,D2D1,D2 và D3D3 hay không?
c) Lấy một điểm trong tam giác OAB (chẳng hạn điểm (1;2)) hoặc một điểm trên cạnh nào đó của tam giác OAB (chẳng hạn điểm (1;149)) và kiểm tra xem tọa độ của các điểm đó có phải là nghiệm của hệ bất phương trình sau hay không:
x≥0
y≥0
x+y≤150

Sản phẩm dự kiến:
a) + Trục Oy có phương trình x = 0
Điểm (1; 0) thỏa mãn 1 > 0, nên miền nghiệm ![]() của bất phương trình
của bất phương trình ![]() là nửa mặt phẳng bờ Oy chứa điểm (1; 0) (tính cả bờ Oy).
là nửa mặt phẳng bờ Oy chứa điểm (1; 0) (tính cả bờ Oy).
+ Trục Oy có phương trình y = 0.
Điểm (0; 1) ) thỏa mãn 1 > 0, nên miền nghiệm![]() của bất phương trình
của bất phương trình ![]() là nửa mặt phẳng bờ Ox chứa điểm (0: 1) (tính cả bờ Ox).
là nửa mặt phẳng bờ Ox chứa điểm (0: 1) (tính cả bờ Ox).
+ Vẽ đường thẳng d: x + y = 150. Tọa độ điểm O(0; 0) thỏa mãn 0 + 0 < 150.
Miền nghiệm ![]() của bất phương trình
của bất phương trình ![]() là nửa mặt phẳng bờ d chứa gốc tọa độ (tính cả bờ d).
là nửa mặt phẳng bờ d chứa gốc tọa độ (tính cả bờ d).
b) Miền tam giác OAB là giao của các miền ![]() ,
, ![]() ,
, ![]() .
.
c) Ta có: 1 > 0, 2 > 0 và 1 + 2 < 150 nên (1; 2) là nghiệm của hệ bất phương trình đã cho. Vì 1 > 0, 149 > 0 và 1 + 149 = 150 nên (1; 149) là nghiệm của hệ bất phương trình đã cho.
HOẠT ĐỘNG 3. ÁP DỤNG VÀO BÀI TOÁN THỰC TIỄN
GV đưa ra câu hỏi: Xét biểu thức F(x, y) = 2x + 3y với (x; y) thuộc miền tam giác OAB ở HĐ2. Toạ độ ba đình là O(0, 0), A(150, 0) và B(0; 150) (H.2.5).

a) Tính giá trị của biểu thức F(x; y) tại mỗi đỉnh O, A và B.
b) Nêu nhận xét về dấu của hoành độ x và tung độ y của điểm (x; y) nằm trong miền tam giác OAB. Từ đó suy ra giá trị nhỏ nhất của F(x; y) trên miền tam giác OAB.
c) Nêu nhận xét về tổng x + y của điểm (X; y) nằm trong miền tam giác OAB. Từ đó suy ra giá trị lớn nhất của F(x, y) trên miền tam giác OAB.
Sản phẩm dự kiến:
a)
Thay tọa độ điểm O(0; 0):
F(0; 0) = 0
Thay tọa độ điểm A(150; 0):
F(150; 0) = 300
Thay tọa độ điểm B(0; 150):
F(0; 150) = 450
b) Nhận xét: x và y đều nhận giá trị không âm.
Giá trị nhỏ nhất của F(x; y) trên miền tam giác OAB là: 0 tại x = y = 0.
c) Nhận xét: ![]() và
và ![]() .
.
Giá trị lớn nhất của F(x; y) trên miền tam giác OAB là: 450 tại x = 0, y = 150.
HOẠT ĐỘNG LUYỆN TẬP
Từ nội dung bài học,GV yêu cầu HS hoàn thành các bài tập trắc nghiệm sau:
Câu 1: Tìm khẳng định sai trong các khẳng định sau:
A. Hệ {x+y≥−1y2−1≤0 không phải là hệ bất phương trình bậc nhất hai ẩn;
B. Hệ {x≥1+y5x+y<0 là hệ bất phương trình bậc nhất hai ẩn;
C. Hệ {x+1+y>0x2+y<0 là hệ bất phương trình bậc nhất hai ẩn;
D. Hệ {12x+2y<7x+3y≤0 là hệ bất phương trình bậc nhất hai ẩn;
Câu 2: Cho hệ bất phương trình {−3x+y>−2x+2y≤1. Và các điểm sau: M(–1 ; 2), N(0; –1), O(0; 0). Có mấy điểm thuộc miền nghiệm của hệ bất phương trình đã cho?
A. 0;
B. 1;
C. 2;
D. 3.
Câu 3: Hệ bất phương trình nào sau đây là hệ bất phương trình bậc nhất hai ẩn ?
A. {3+3y≥02x≤0
B. {x2+3y≥22x+y≤−1
C. {4x+3y−1≥0x+y3>0
D. {−x2+3y≥52x+y≤−1
Câu 4: Giá trị nhỏ nhất Fmin của biểu thức F= –x + y trên miền xác định bởi hệ ⎧⎩⎨⎪⎪−2x+y≥2y−x≤4x+2y≥5 là:
A. Fmin = 115;
B. Fmin = 0;
C. Fmin = 2;
D. Fmin = 4.
Câu 5: Cho hệ ⎧⎩⎨⎪⎪x+y≤14x−y≤2x≥0. Giá trị lớn nhất của biểu thức P = x – y trên miền nghiệm của hệ đã cho là:
A. – 1;
B. 15
C. 2;
D. 1
Sản phẩm dự kiến:
Câu 1 - C | Câu 2 - C | Câu 3 - A | Câu 4 - A | Câu 5 - C |
HOẠT ĐỘNG VẬN DỤNG
Vận dụng kiến thức, GV yêu cầu HS hoàn thành bài tập sau:
Câu 1: Một gia đình cần ít nhất 900 đơn vị protein và 400 đơn vị lipit trong thức ăn mỗi ngày. Mỗi kilôgam thịt bò chứa 800 đơn vị protein và 200 đơn vị lipit. Mỗi kilôgam thịt lợn chứa 600 đơn vị protein và 400 đơn vị lipit. Biết rằng gia đình này chỉ mua nhiều nhất là 1,6 kg thịt bò và 1,1 kg thịt lợn, giá tiền 1 kg thịt bò là 250 nghìn đồng, 1 kg thịt lợn là 160 nghìn đồng. Giả sử gia đình đó mua x kilôgam thịt bò và y kilôgam thịt lợn.
a) Viết các bất phương trình biểu thị các điều kiện của bài toán thành một hệ bất phương trình rồi xác định miền nghiệm của hệ đó.
b) Gọi F (nghìn đồng) là số tiền phải trả cho x kilôgam thịt bò và y kilôgam thịt lợn. Hãy biểu diễn F theo x và y.
c) Tìm số kilôgam thịt mỗi loại mà gia đình cần mua để chi phí là ít nhất.
Câu 2: Một cửa hàng có kế hoạch nhập về hai loại máy tính A và B, giá mỗi chiếc lần lượt là 10 triệu đồng và 20 triệu đồng với số vốn ban đầu không vượt quá 4 tỉ đồng. Loại máy A mang lại lợi nhuận 2,5 triệu đồng cho mỗi máy bán được và loại máy B mang lại lợi nhuận là 4 triệu đồng mỗi máy. Cửa hàng ước tính rằng tổng nhu cầu hàng tháng sẽ không vượt quá 250 máy. Giả sử trong một tháng cửa hàng cần nhập số máy tính loại A là x và số máy tính loại B là y.
a) Viết các bất phương trình biểu thị các điều kiện của bài toán thành một hệ bất phương
trình rồi xác định miền nghiệm của hệ đó.
b) Gọi F (triệu đồng) là lợi nhuận mà cửa hàng thu được trong tháng đó khi bán x máy tính loại A và y máy tính loại B. Hãy biểu diễn F theo x và y.
c) Tìm số lượng máy tính mỗi loại cửa hàng cần nhập về trong tháng đó đề lợi nhuận thu được là lớn nhất.
Bài toán 2: (SGK - tr28, 29)
Trên chỉ là 1 phần của giáo án. Giáo án khi tải về có đầy đủ nội dung của bài. Đủ nội dung của học kì I + học kì II
Đủ kho tài liệu môn học
=> Tài liệu sẽ được gửi ngay và luôn
Cách tải:
- Bước 1: Chuyển phí vào STK: 1214136868686 - cty Fidutech - MB
- Bước 2: Nhắn tin tới Zalo Fidutech - nhấn vào đây để thông báo và nhận tài liệu
Xem toàn bộ: Trọn bộ giáo án và PPT Toán 10 cánh diều
TÀI LIỆU GIẢNG DẠY TOÁN 10 KẾT NỐI TRI THỨC
Giáo án Toán 10 kết nối tri thức đủ cả năm
Giáo án điện tử toán 10 kết nối tri thức
Trò chơi khởi động Toán 10 kết nối tri thức
Video AI khởi động Toán 10 kết nối tri thức hấp dẫn
Trắc nghiệm toán 10 kết nối tri thức
Đề thi toán 10 kết nối tri thức
File word đáp án Toán 10 kết nối tri thức
Bài tập file word Toán 10 Kết nối
Kiến thức trọng tâm toán 10 kết nối tri thức
Đề kiểm tra 15 phút Toán 10 kết nối tri thức
Phiếu học tập theo bài Toán 10 kết nối tri thức cả năm
Trắc nghiệm đúng sai Toán 10 kết nối tri thức cả năm
Trắc nghiệm dạng câu trả lời ngắn Toán 10 kết nối tri thức cả năm
TÀI LIỆU GIẢNG DẠY TOÁN 10 CHÂN TRỜI SÁNG TẠO
Giáo án Toán 10 chân trời sáng tạo đủ cả năm
Giáo án điện tử toán 10 chân trời sáng tạo
Trò chơi khởi động Toán 10 chân trời sáng tạo
Video AI khởi động Toán 10 chân trời sáng tạo hấp dẫn
Trắc nghiệm toán 10 chân trời sáng tạo
Đề thi toán 10 chân trời sáng tạo
File word đáp án Toán 10 chân trời sáng tạo
Bài tập file word toán 10 chân trời sáng tạo
Kiến thức trọng tâm toán 10 chân trời sáng tạo
Đề kiểm tra 15 phút Toán 10 chân trời sáng tạo
Phiếu học tập theo bài Toán 10 chân trời sáng tạo cả năm
Trắc nghiệm đúng sai Toán 10 chân trời sáng tạo cả năm
Trắc nghiệm dạng câu trả lời ngắn Toán 10 chân trời sáng tạo cả năm
TÀI LIỆU GIẢNG DẠY TOÁN 10 CÁNH DIỀU
Giáo án Toán 10 cánh diều đủ cả năm
Giáo án điện tử toán 10 cánh diều
Trò chơi khởi động Toán 10 cánh diều
Video AI khởi động Toán 10 cánh diều hấp dẫn
Trắc nghiệm toán 10 cánh diều
Đề thi toán 10 cánh diều
File word đáp án Toán 10 cánh diều
Kiến thức trọng tâm toán 10 cánh diều
Bài tập file word toán 10 cánh diều
Đề kiểm tra 15 phút Toán 10 cánh diều
Phiếu học tập theo bài Toán 10 cánh diều cả năm
Trắc nghiệm đúng sai Toán 10 cánh diều cả năm
Trắc nghiệm dạng câu trả lời ngắn Toán 10 cánh diều cả năm
