Giáo án và PPT Toán 7 kết nối Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác

BÀI 35. SỰ ĐỒNG QUY CỦA BA ĐƯỜNG TRUNG TRỰC, 

BA ĐƯỜNG CAO TRONG MỘT TAM GIÁC

HOẠT ĐỘNG KHỞI ĐỘNG

- GV yêu cầu HS đọc tình huống mở đầu 

Có thể coi ba ngôi nhà của ba anh em trong một khu vườn là ba đỉnh của một tam giác (không tù). Họ muốn khoan một giếng chung trong vườn cách đều ba ngôi nhà (H9.36). 

Em có thể giúp họ chọn địa điểm để khoan giếng không?

- Giáo viên gợi ý: Địa điểm khoan giếng cần đảm bảo điều kiện gì?

HOẠT ĐỘNG HÌNH THÀNH KIẾN THỨC

Hoạt động 1: Sự đồng quy của ba đường trung trực trong một tam giác

- GV đặt câu hỏi hướng dẫn HS tìm hiểu: Trình bày định nghĩa đường trung trực của tam giác.

- GV cho  HS tìm hiểu "Sự đồng quy của ba đường trung trực", yêu cầu HS thực hành và trả lời câu hỏi theo nhóm bốn các HĐ1, HĐ2.

- GV đưa ra câu hỏi: Trình bày Định lí 1 về sự đồng quy của ba đường trung trực.

- GV lưu ý cho HS phần Nhận xét - SGK.

- GV hướng dẫn, yêu cầu HS đọc hiểu Ví dụ 1 theo nhóm đôi và trình bày vào vở để hiểu và biết cách trình bày.

- GV yêu cầu HS tự hoàn thành Luyện tập 1 để hình thành và rèn luyện kĩ năng sử dụng Định lí 1.

- GV tổ chức cho HS vận dụng kiến thức đã học ở trên để trả lời câu hỏi trong tình huống mở đầu, hoàn thành bài Vận dụng 1.

- GV cho HS luyện kĩ năng vận dụng tính chất của đường trung trực của đoạn thẳng vừa nhắc lại ở trên để trao đổi thực hiện Thử thách nhỏ.

Sản phẩm dự kiến:

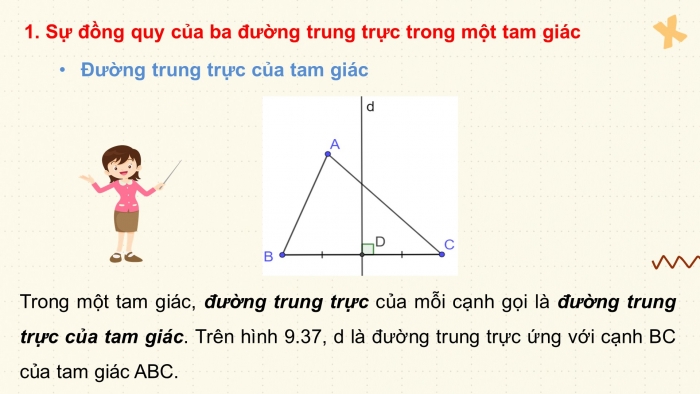
• Đường trung trực của tam giác

Trong một tam giác, đường trung trực của mỗi cạnh gọi là đường trung trực của tam giác. Trên hình 9.37, d là đường trung trực ứng với cạnh BC của tam giác ABC.

? 

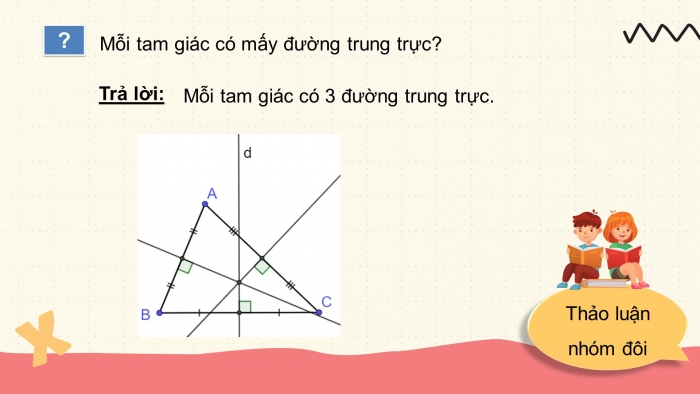
Mỗi tam giác có 3 đường trung trực.

• Sự đồng quy của ba đường trung trực

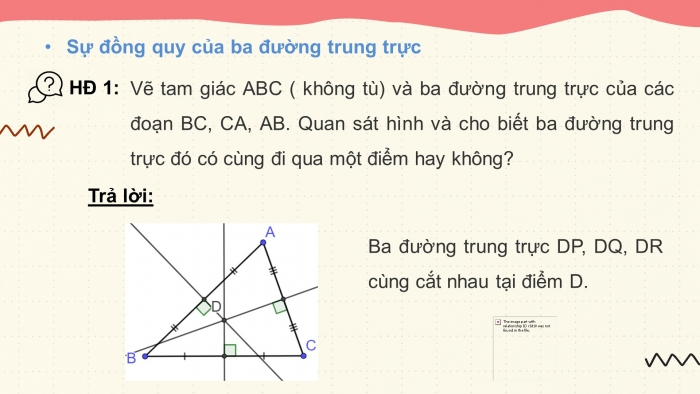
HĐ1. 

Ba đường trung trực DP, DQ, DR cùng cắt nhau tại điểm D.

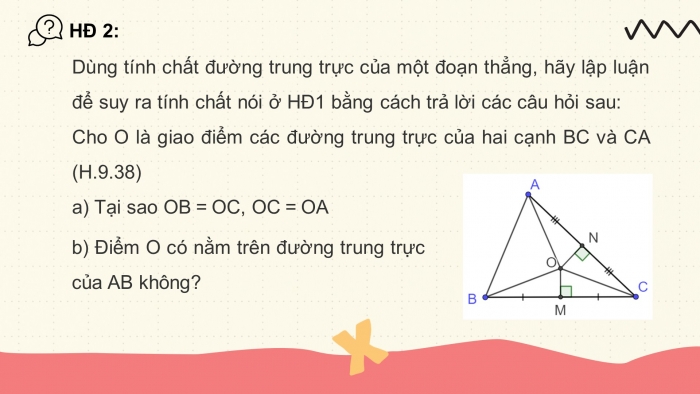
HĐ2. 

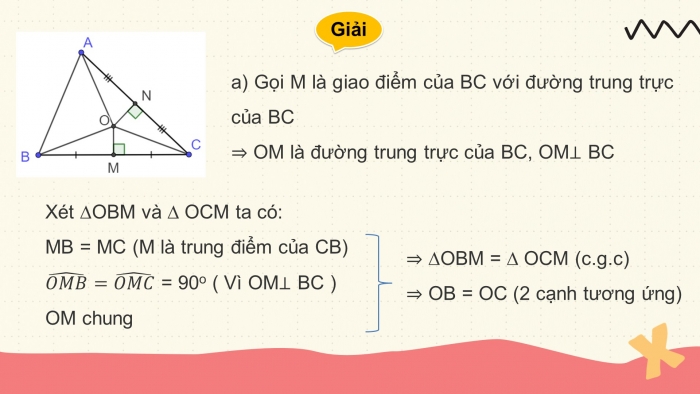
a) Gọi M là giao điểm của BC với đường trung trực của BC

=> OM là đường trung trực của BC, OM⊥ BC

Xét ∆OBM và ∆ OCM ta có:

2 tam giác đều vuông tại M

MB= MC ( M là trung điểm của CB)

OM chung

=> ∆OBM = ∆ OCM => OB= OC

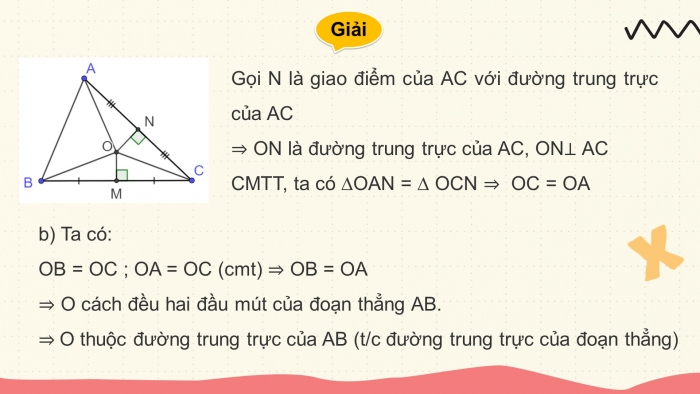
Tương tự, ta có OC= OA

b) Từ câu a ta có OA=OB

=> ∆OAB là tam giác cân tại O

Kẻ ON ⊥ AB=> ON là đường trung tuyến của AB và N là trung điểm của AB

=> O thuộc đường trung trực của AB

Định lí 1:

Ba đường trung trực của một tam giác đồng quy tại một điểm. Điểm này cách đều ba đỉnh của tam giác.

Nhận xét:

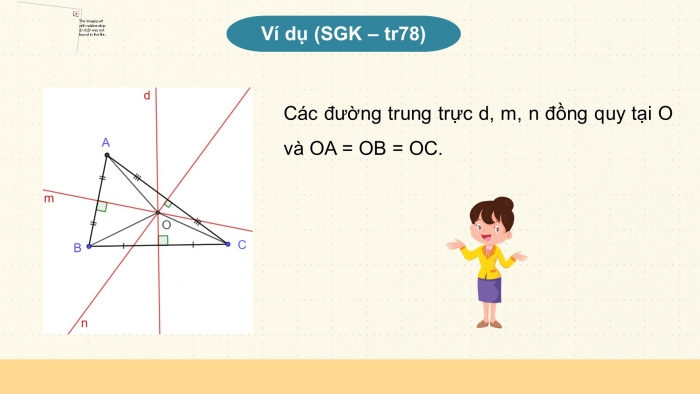
Vì giao điểm O của ba đường trung trực trong tam giác ABC cách đều ba đỉnh của tam giác đó (OA = OB = OC) nên có một đường tròn tâm O đi qua ba đỉnh A, B, C. (H.9.40)

Ví dụ 1: (SGK – tr78)

Luyện tập 1:

Gọi AN, CM, BP là 3 đường trung tuyến của tam giác đều ABC, giao nhau ở điểm G

Xét ∆ ANB và ∆ ANC, có:

 AN chung

NB= NC

AB= AC

=>∆ ANB = ∆ ANC

=> 

=

=> AN hay AG là đường phân giác của

Tương tự BP hay BG là đường phân giác của

=> G cách đều 3 cạnh AB, AC, BC mag G là trọng tâm

=> G là giao điểm của 3 đường trung trực => G cách đều 3 điểm A,B,C

Vận dụng 1:

- Ba ngôi nhà không thẳng hàng nên tạo thành 1 tam giác, ta gọi là tam giác ABC.

- Điểm khoan giếng cách đều 3 ngôi nhà khi và chỉ khi điểm khoan giếng là giao điểm của 3 đường trung trực của tam giác ABC.

Vậy, ta cần vẽ 2 đường trung trực của tam giác ABC, chúng cắt nhau tại đâu thì đó là điểm cần khoan giếng.

Thử thách nhỏ:

Vì Q cách đều 3 đỉnh của tam giác ABC nên GA=GB=GC

Vì QA = QB nên Q nằm trên đường trung trực của đoạn thẳng AB (tính chất đường trung trực của đoạn thẳng).

Vì QA = QC nên Q nằm trên đường trung trực của đoạn thẳng AC (tính chất đường trung trực của đoạn thẳng).

Vì QB = QC nên Q nằm trên đường trung trực của đoạn thẳng BC (tính chất đường trung trực của đoạn thẳng).

Vậy Q là giao điểm của 3 đường trung trực của tam giác ABC.

Hoạt động 2: Sự đồng quy của ba đường cao trong một tam giác

- GV đưa ra câu hỏi: Trình bày khái niệm đường cao trong tam giác.

- GV cho  HS tìm hiểu "Sự đồng quy của ba đường cao", yêu cầu HS thực hành và trả lời câu hỏi HĐ3.

- GV đưa ra câu hỏi: Trình bày Định lí 2 về sự đồng quy của ba đường phân giác.

- GV lưu ý cho HS phần Chú ý  - SGK – tr 80 về vị trí của trực tâm trong tam giác nhọn, tam giác vuông và tam giác tù.

- GV hướng dẫn, yêu cầu HS đọc hiểu Ví dụ 2 theo nhóm đôi và trình bày vào vở.

- GV yêu cầu HS tự hoàn thành Luyện tập 2 để hình thành và rèn luyện kĩ năng sử dụng Định lí 2.

Sản phẩm dự kiến:

• Đường cao của tam giác

Trong hình 9.42, đoạn thẳng AI kẻ từ đỉnh A, vuông góc với cạnh đối diện BC là một đường cao của tam giác ABC. Ta còn nói AI là đường cao xuất phát từ đỉnh A (hay đường cao ứng với cạnh BC).

?

Mỗi tam giác có 3 đường cao.

( Vì ứng với mỗi cạnh của tam giác, ta có 1 đường cao).

• Sự đồng quy của ba đường cao

HĐ3: 

Ba đường cao AN, BP, CM cùng đi qua điểm H.

Định lí 2:

Ba đường cao của tam giác đồng quy tại một điểm.

Chú ý:

a) Điểm đồng quy của ba đường cao của một tam giác gọi là trực tâm của tam giác đó. 

b) Gọi H là trực tâm của tam giác ABC (H.9.44), ta có: 

• Khi ABC là tam giác nhọn thì H nằm bên trong tam giác. 
• Khi ABC là tam giác vuông tại A thì H trùng với A (kí hiệu là H 
• A).
•  Khi ABC là tam giác tù thì H nằm bên ngoài tam giác.

Ví dụ 2: SGK – tr80

Luyện tập 2:

a)

Gọi AD là đường trung tuyến và đường phân giác tại đỉnh A của ∆ ABC

Xét  ∆ ADB và ∆ ADC, có:

AB=AC

DB=DC

AD chung

=>∆ ADB = ∆ ADC (c.c.c)

=>  =

Mà + = 180^o

=> = = 90^o

=>AD vuông góc với BC

mà DA=DB

=>AD là đường trung trực của tam giác ABC

b) 

G là điểm cách đều 3 đỉnh của tam giác ABC đều

GM, GN, GP là khoảng cách từ G đến AB, BC, AC

Xét ∆ AGB và ∆ AGC, có:

AG chung

GB= GC

AB= AC

=> ∆ AGB = ∆ AGC (c.c.c)

=> =

=> AG là đường phân giác của

Tương tự ta có: CG là đường phân giác của

=> G là điểm giao nhau giữa 2 đường phân giác AG và CG

=> G cách đều 3 cạnh AB,AC, BC.

Lưu ý:

Trong tam giác cân tại A, đường cao xuất phát từ đỉnh A đồng thời là đường trung trực, đường phân giác, đường trung tuyến của tam giác đó.

HOẠT ĐỘNG LUYỆN TẬP

Từ nội dung bài học, GV yêu cầu HS hoàn thành các bài tập trắc nghiệm sau:

Câu 1: Cho ΔABC, hai đường cao AM và BN cắt nhau tại H. Em chọn phát biểu đúng:

A. H là trọng tâm của ΔABC

B. H là tâm đường tròn nội tiếp ΔABC

C. CH là đường cao của ΔABC

D. CH là đường trung trực của ΔABC

Câu 2: Đường cao của tam giác đều cạnh 4 có bình phương độ dài đường cao là

A. 16

B. 12

C. 14

D. 10

Câu 3: Cho ΔABC nhọn, hai đường cao BD và CE. Trên tia đối của tia BD lấy điểm I sao cho BI = AC. Trên tia đối của tia CE lấy điểm K sao cho CK = AB. Chọn câu đúng

A. AI > AK

B. AI < AK

C. AI = 2AK

D. AI = AK

Câu 4: Cho  ΔABC cân tại A, trung tuyến AM. Biết  BC = 24cm, AM = 5cm. Tính độ dài các cạnh AB và AC

A. AB = AC = 13cm

B. AB = AC = 14cm

C. AB = AC = 15cm

D. AB = AC = 16cm

Câu 5: Cho tam giác ABC có AC > AB. Trên cạnh AC lấy điểm E sao cho CE = AB. Các đường trung  trực của BE và AC cắt nhau tại O. Chọn câu đúng

A. ΔABO = ΔCOE

B. ΔBOA = ΔCOE

C. ΔAOB = ΔCOE

D. ΔABO = ΔCEO

Sản phẩm dự kiến:

HOẠT ĐỘNG VẬN DỤNG

Vận dụng kiến thức, GV yêu cầu HS trả lời câu hỏi:

Câu 1: Cho tam giác ABC vuông tại A, kẻ đường cao AH. Trên cạnh AC lấy điểm K sao cho AK = AH. Kẻ KD  AC (D . Chứng minh AD là đường trung trực của đoạn thẳng HK.

Câu 2: Nếu một tam giác có đường trung tuyến đồng thời là đường trung trực thì tam giác đó là tam giác gì?