Giáo án điện tử toán 10 cánh diều bài 3: Các số đặc trưng đo mức độ phân tán cho mẫu số liệu không ghép nhóm

BÀI 3: CÁC SỐ ĐẶC TRƯNG ĐO MỨC ĐỘ PHÂN TÁN CHO MẪU SỐ LIỆU KHÔNG GHÉP NHÓM

1. KHỞI ĐỘNG

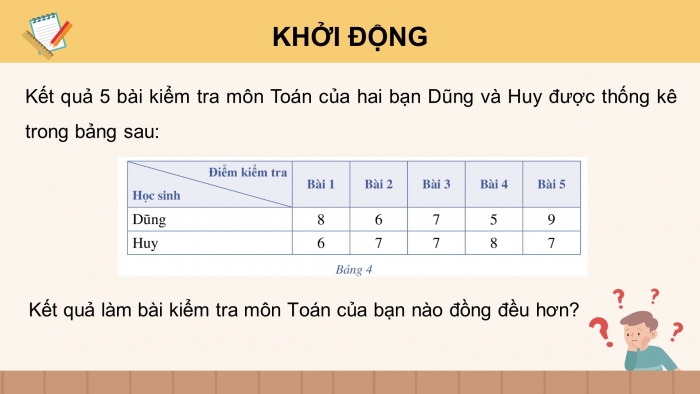
Kết quả 5 bài kiểm tra môn Toán của hai bạn Dũng và Huy được thống kê trong bảng sau:

(1. Bảng 4)

Kết quả làm bài kiểm tra môn Toán của bạn nào đồng đều hơn?

1. NỘI DUNG BÀI HỌC
2. Khoảng biến thiên. Khoảng tứ phân vị
3. Phương sai

III. Độ lệch chuẩn.

1. Tính hợp lí của số liệu thống kê

1. PHẦN TRIỂN KHAI KIẾN THỨC
2. Khoảng biến thiên. Khoảng tứ phân vị.
3. Định nghĩa

Em hãy đọc nội dung HĐ1 và trả lời câu hỏi.

HĐ1:

Kết quả của 11 lần đo được thống kê trong mẫu số liệu sau:

 (1)

1. a) Tìm hiệu giữa số đo lớn nhất và số đo nhỏ nhất.
2. b) Sắp xếp các số liệu của mẫu (1) theo thứ tự tăng dần. Tìm các giá trị Q­₁, Q­₂, Q₃là tứ phân vị của mẫu đó. Sau đó, tìm hiệu Q₃– Q₁.

G:

1. Trong mẫu số liệu (1), hiệu giữa số đo lớn nhất và số đo nhỏ nhất là:

R = x_max – x_min = 16 – 2  = 14

1. Sắp xếp các số liệu của mẫu (1) theo thứ tự tăng dần, ta được:

2   5   6   7   8   9   10   11   12   14   16

Vậy Q₁ = 6; Q₂ = 9; Q₃ = 12.

Suy ra  = Q₃ – Q₁ = 12 – 6 = 6.

Kết luận:

+ Trong một mẫu số liệu, khoảng biến thiên là hiệu số giữa giá trị lớn nhất và giá trị nhỏ nhất của mẫu số liệu đó.

Ta có thể tính khoảng biến thiên R của mẫu số liệu theo công thức sau:

R = x_max – x_min, trong đó x_max là giá trị lớn nhất, x_min là giá trị nhỏ nhất của mẫu số liệu đó.

+ Giả sử Q₁, Q₂, Q₃ là tứ phân vị của mẫu số liệu. Ta gọi hiệu  là khoảng tứ phân vị của mẫu số liệu đó.

Chú ý:

Khoảng tứ phân vị của mẫu số liệu còn gọi là khoảng trải giữa (tiếng Anh là InterQuartile Range – IQR) của mẫu số liệu đó.

Em hãy đọc nội dung Ví dụ 1 và trả lời câu hỏi.

Ví dụ 1 (SGK – tr36)

Mẫu số liệu thống kê chiều cao (đơn vị: mét) của 15 cây bạch đàn là:

   (2)

1. a) Tìm khoảng biến thiên của mẫu số liệu (2).
2. b) Tìm khoảng tứ phân vị của mẫu số liệu (2).

Giải

1. a) Trong mẫu số liệu (2), số lốn nhất là 9,0 và số bé nhất là 6,3 . Vậy khoảng biến thiên của mẫu số liệu (2) là:
2. b) Sắp xếp các số liệu của mẫu (2) theo thứ tự tăng dần, ta được:

Do đó .

Vậy khoảng tứ phân vị của mẫu số liệu (2) là: .

2. Ý nghĩa
3. Ý nghĩa của khoảng biến thiên: Khoảng biến thiên của mẫu số liệu phản ánh sự “dao động”, “sự dàn trải” của các số liệu trong mẫu đó.
4. Ý nghĩa của khoảng tứ phân vị: Khoảng tứ phân vị là một đại lượng cho biết mức độ phân tán của 50% số liệu chính giữa của mẫu số liệu đã sắp xếp và có thể giúp xác định các giá trị bất thường của mẫu số liệu đó.

1. Phương sai
2. Định nghĩa

Em hãy đọc nội dung HĐ2 và trả lời câu hỏi.

HĐ2:

Số liệu thống kê kết quả 5 bài kiểm tra môn Toán của bạn Dũng là:  (xem Bảng 4).

(1.bảng 4)

Số trung bình cộng của mẫu số liệu (3) là:

1. a) Tính các độ lệch sau: .
2. b) Tính bình phương các độ lệch và tính trung bình cộng của chúng.

g

1. Ta có:

8 – 7 = 1; 6 – 7 = – 1; 7 – 7 = 0; 5 – 7 = – 2; 9 – 7 = 2.

1. Bình phương các độ lệch là:

(8 – 7)² = 1; (6 – 7)² = 1; (7 – 7)² = 0; (5 – 7)² = 4; (9 – 7)² = 4.

Trung bình cộng của bình phương các độ lệch là:

s² =

Lưu ý: Mỗi hiệu giữa số liệu và số trung bình cộng gọi là độ lệch của số liệu đó đối với số trung bình cộng.

Kết luận:

Cho mẫu số liệu thống kê có n giá trị x₁, x₂, …, x_n và số trung bình cộng là

Ta gọi số:

s² =  là phương sai của mẫu số liệu trên.

Nhận xét:

- Khi có các số liệu bằng nhau, ta có thể tính phương sai theo công thức sau:

+ Phương sai của mẫu số liệu thống kê trong bảng phân bố tần số là:

s² =

trong đó n = n₁ + n₂ +…+ n_k;  là số trung bình cộng của các số liệu đã cho.

(2.bảng tần số)

+ Phương sai của mẫu số liệu thống kê trong bảng phân bố tần số tương đối là:

s² =

Trong đó,  là số trung bình cộng của các số liệu đã cho.

(3.bảng tần số tương đối)

- Trong thực tế, người ta còn dùng công thức sau để tính phương sai của một mẫu số liệu:

² =

Trong đó, x_i là giá trị của quan sát thứ i;  là giá trị trung bình và n là số quan sát trong mẫu số liệu đó.

Em hãy đọc nội dung Ví dụ 2 và trả lời câu hỏi.

Ví dụ 2 (SGK – tr36)