Giáo án điện tử toán 10 cánh diều bài 2: Giải tam giác. tính diện tích tam giác (2 tiết)

CHÀO MỪNG CÁC EM ĐẾN VỚI BUỔI HỌC!
Từ xa xưa, con người đã cần đo đạc các khoảng cách mà không thể đo trực tiếp được. Chẳng hạn, để đo khoảng cách từ vị trí A trên bờ biển tới một hòn đảo (hay còn tàu, ...) trên biển, người xưa đã tìm ra một cách đo khoảng cách đó như sau:
Từ vị trí A, đo góc nghiêng α so với bờ biển tới một vị trí C quan sát được trên đảo. Sau đó di chuyển dọc bờ biển đến vị trí B cách A một khoảng d và tiếp tục đo góc nghiêng β so với bờ biển tới vị trí C đã chọn. Bằng cách giải tam giác ABC, họ tính được khoảng cách AC.
Giải tam giác được hiểu như thế nào?
BÀI 2: GIẢI TAM GIÁC. TÍNH DIỆN TÍCH TAM GIÁC (2 tiết)
I. GIẢI TAM GIÁC
Giải tam giác là tính các cạnh và các góc của tam giác dựa trên những dữ kiện cho trước.
HĐ1
Cho tam giác ABC có AB=c, AC=b, A ̂=α. Viết công thức tính BC theo b,c, α.
Giải
Áp dụng định lí côsin trong tam giác ABC có:
BC^2=AB^2+AC^2-2.AB.AC.cos⁡A
=c^2+b^2-2.b.c.cos⁡α
⇒BC=√(c^2+b^2-2bc cos⁡α )
Ví dụ 1
Cho tam giác ABC có AB=15, AC=35, A ̂=60°. Tính cạnh BC (làm tròn kết quả đến hàng phần mười).
Giải
Áp dụng định lí côsin trong tam giác ABC có:
BC^2=AB^2+AC^2-2.AB.AC.cos⁡A
=15^2+35^2-2.15.35.cos⁡〖60°〗
=925
⇒BC=√925≈30,4.
HĐ2
Cho tam giác ABC có AB=c, AC=b, BC=a. Viết công thức tính cos⁡A theo a,b,c.
Giải
Áp dụng định lí côsin trong tam giác ABC:
cos⁡A=(b^2+c^2-a^2)/2bc
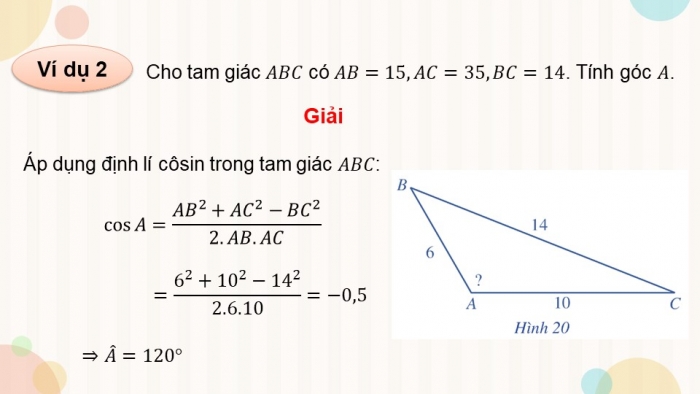
Ví dụ 2
Cho tam giác ABC có AB=15, AC=35, BC=14. Tính góc A.
Giải
Áp dụng định lí côsin trong tam giác ABC:
cos⁡A=(〖AB〗^2+〖AC〗^2-〖BC〗^2)/(2.AB.AC)
=(6^2+10^2-14^2)/2.6.10=-0,5
⇒A ̂=120°
HĐ3
Cho tam giác ABC có BC=a, B ̂=α, C ̂=β. Viết công thức tính AB và AC theo a,α,β.
Giải
A ̂=180^o-(B ̂+C ̂)=180^o-(α+β)⇒sin⁡A=sin⁡( α+β)
Áp dụng định lí sin trong tam giác ABC:
BC/sin⁡A =AC/sin⁡B =AB/sin⁡C =2R⇒a/(sin⁡( α+β))=AC/sin⁡α =AB/sin⁡β =2R
⇒AC=(a.sin⁡α)/(sin⁡( α+β));AB=(a.sin⁡β)/(sin⁡( α+β))
Ví dụ 3
Cho tam giác ABC có BC=100, B ̂=60°, C ̂=40°. Tính góc A và các cạnh AB, AC (làm tròn kết quả đến hàng phần mười) của tam giác đó.
Giải
Ta có: A ̂=180°-(B ̂+C ̂ )=180°-(60°+40)=80°
Áp dụng định lí sin trong tam giác ABC:
⇒AB=(BC.sin⁡C)/sin⁡A =(100.sin⁡〖40°〗)/sin⁡〖80°〗 ≈65,3
AC=(BC.sin⁡B)/sin⁡A =(100.sin⁡〖60°〗)/sin⁡〖80°〗 ≈87,9
II. TÍNH DIỆN TÍCH TAM GIÁC
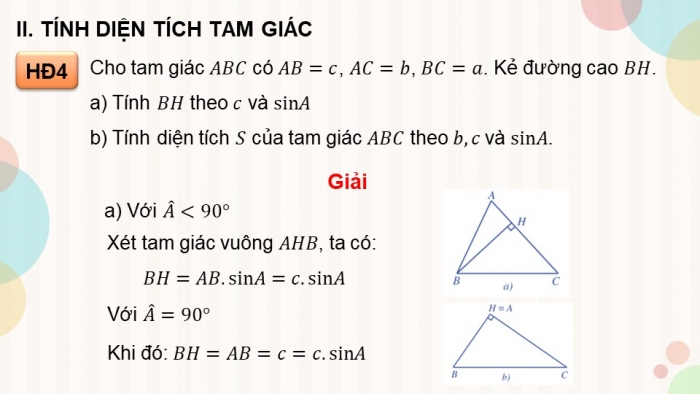
HĐ4
Cho tam giác ABC có AB=c, AC=b, BC=a. Kẻ đường cao BH.
a) Tính BH theo c và sinA
b) Tính diện tích S của tam giác ABC theo b, c và sinA.
Giải
a) Với A ̂<90°
Xét tam giác vuông AHB, ta có:
BH=AB.sinA=c.sinA
Với A ̂=90°
Khi đó: BH=AB=c=c.sinA
Với A ̂>90°
Xét tam giác vuông AHB,
ta có: (BAH) ̂=180°-A ̂
⇒BH=AB.sin(180°-A ̂ )=AB.sinA=c.sinA
b) Ta có:
S=1/2 AC.BH=1/2 bc sin⁡A
Kết luận:
Cho tam giác ABC có BC=a, CA=b, AB=c. Khi đó, diện tích S của tam giác ABC là:
S=1/2 bc sin⁡A=1/2 ca sin⁡B=1/2 ab sin⁡C
Ví dụ 4
Cho tam giác ABC có BC=7,5 ;AC=15,5; A ̂=75°. Tính diện tích S của tam giác ABC(làm tròn kết quả đến hàng phần mười).
Giải
Ta có:
S=1/2 AB.AC.sin⁡A
=1/2.7,5.15,5.sin⁡〖75°〗
≈56,1
Luyện tập 1
Cho tam giác ABC có AB=12, B ̂=60°, C ̂=45°. Tính diện tích của tam giác ABC.
Giải
Ta có: A ̂=180°-B ̂-C ̂=75°
Áp dụng định lí sin trong tam giác ABC:
AB/sin⁡C =AC/sinB⇒AC=(AB.sinB)/sinC=6√6
Diện tích tam giác ABC là:
S=1/2.AB.AC.sinA≈85,2.
HĐ5
Cho tam giác ABC có AB=c, AC=b, BC=a và diện tích S
a) Từ định lí côsin, chứng tỏ rằng:
sin⁡A=2/bc √(p(p-a)(p-b)(p-c) ),
p=(a+b+c)/2
b) Bằng cách sử dụng công thức S=1/2 bc sin⁡A, hãy chứng tỏ rằng S=√(p(p-a)(p-b)(p-c) )
Giải
a) Theo định lí côsin, ta có:
cos⁡A=(b^2+c^2-a^2)/2bc
Mà 〖sin〗^2⁡A+〖cos〗^2⁡A=1
⇒sin^2⁡A=(4b^2 c^2-(b^2+c^2-a^2 )^2)/(4b^2 c^2 )
⇒sin⁡A=1/2bc √((2bc)^2-(b^2+c^2-a^2 )^2 )
Xét T=(2bc)^2-(b^2+c^2-a^2 )^2
=(2bc+b^2+c^2-a^2 )(2bc-b^2-c^2+a^2 )
=[(b+c)^2-a^2 ][a^2-(b-c)^2 ]
=(b+c-a)(b+c+a)(a-b+c)(a+b-c)
Ta có: a+b= c=2p
⇒{█(&b+c-a=2(p-a)@&a-b+c=2(p-b)@&a+b-c=2(p-c))┤
⇒T=4√(p(p-a)(p-b)(p-c))
sin⁡A=2/bc √(p(p-a)(p-b)(p-c) )
b) Diện tích S theo các cạnh của tam giác ABC
S=1/2 bc sin⁡A
=1/2 bc.2/bc √(p(p-a)(p-b)(p-c))
=√(p(p-a)(p-b)(p-c))
Kết luận:
Cho tam giác ABC có BC=a, CA=b, AB=c, p=(a+b+c)/2.
Khi đó, diện tích S của tam giác ABC là:
S=√(p(p-a)(p-b)(p-c))
Ví dụ 5
Mảnh vườn hình tam giác của gia đình bạn Nam có chiều dài các cạnh là MN=20 m, NP=28 m, MP=32 m. Hỏi diện tích mảnh vườn của gia đình bạn Nam là bao nhiêu mét vuông (làm tròn đến hàng phần mười)?
Giải
p=(20+28+32)/2=40 (m)
Diện tích mảnh vườn là:
S=√(40(40-20)(40-28)(40-32) )

28≈277,1 (m^2 )
III. ÁP DỤNG VÀO BÀI TOÁN THỰC TIỄN
Ví dụ 6
Đứng ở vị trí A trên bờ biển, bạn Minh đo được góc nghiêng so với bờ biển tới một vị trí C trên đảo là 30°. Sau đó di chuyển dọc bờ biển đến vị trí B cách A một khoảng 100m và đo được góc nghiêng so với bờ biển tới vị trí C đã chọn là 40. Tính khoảng cách từ vị trí C trên đoả tới bờ biển theo đơn vị mét (làm tròn kết quả đến hàng phần mười).
Giải
Xét tam giác ABC, ta có:
C ̂=180°-(30°+40°)=110°
Áp dụng định lí sin trong tam giác ABC, ta có:
AC/sin⁡B =AB/sin⁡C
⇒AC=(AB.sin⁡B)/sin⁡C =(100.sin⁡〖40°〗)/sin⁡〖110°〗 ≈68,4(m)
Xét tam giác vuông AHC, ta có: CH=AC.sin⁡〖30°〗≈68,4. 0,5≈34,2 (m)
Vậy khoảng cách từ vị trí C trên đảo tới bờ biển xấp xỉ 34,2 m.
Ví dụ 7
Trong lần đến tham quan tháp Eiffel (ở thủ đô Paris, Pháp), bạn Phương muốn ước tính độ cao của tháp. Sau khi quan sát, bạn Phương đã minh hoạ lại kết quả đo đạc ở Hình 27. Em hãy giúp bạn Phương tính độ cao h của tháp Eiffel theo đơn vị mét (làm tròn kết quả đến hàng đơn vị).
Giải
Xét tam giác ABD, sử dụng tính chất góc ngoài, ta có:
(ABD) ̂=70°-50°=20°
Áp dụng định lí sin cho tam giác ABD, ta có:
BD/sin⁡(BAD) ̂ =AB/sin⁡(ADB) ̂
⇒BD=(154.sin⁡〖50°〗)/sin⁡〖20°〗 ≈345 (m)
Xét tam giác vuông BCD, ta có:
CD=BD.sin⁡(CBD) ̂ ≈345.sin⁡〖70°〗≈324 (m)
Vậy chiều cao h của tháp Eiffel khoảng 324 m.
Từ trên nóc của một toà nhà cao 18,5 m, bạn Nam quan sát một cái cây cách toà nhà 30 m và dung giác kế đo được góc lệch giữa phương quan sát gốc cây và phương ngang là 34°, góc lệch giữa phương quan sát ngọn cây và phương nằm ngang là 24°. Biết chiều cao của chân giác kế là 1,5 m. Chiều cao của cái cây là bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?
Giải
Gọi A là vị trí đặt mắt quan sát bằng giác kế, B là vị trí ngọn cây, D là vị trí gốc cây.
Gọi C là hình chiếu vuông góc của A lên BD.
Trường hợp 1: Cây cao hơn vị trí quan sát.
Gọi góc (BAC) ̂=β=24°, (DAC) ̂=α=34°
Áp dụng định lí sin trong tam giác ABC:
BC/sin⁡β =AC/sin⁡B
Mà B ̂=90°-β=66°
⇒BC/(sin24°)=30/(sin66°)
Vậy chiều cao của cây là:
BD=BC+CD≈13,4 +18,5+1,5=33,4 (m)
Trường hợp 2: Cây thấp hơn vị trí quan sát.
Gọi góc (BAC) ̂=β=24°, (DAC) ̂=α=34°
Áp dụng định lí sin trong tam giác ABC:
BC/sinβ=AC/(sin(ABC) ̂ )
⇒BC/(sin24°)=AC/(sin66°)
⇒BC≈13,4 (m)
Vậy chiều cao của cây là:
BD=DC-BC≈18,5+1,5-13,4=6,6 (m)