Giáo án PPT dạy thêm Toán 8 cánh diều Bài 1: Hình chóp tam giác đều

CHÀO ĐÓN CÁC EM TỚI TIẾT HỌC MÔN TOÁN NGÀY HÔM NAY!

KHỞI ĐỘNG

Thế nào là hình chóp tam giác đều? Hãy cho ví dụ.

Nêu công thức tính diện tích xung quanh và thể tích của hình chóp tam giác đều.

CHƯƠNG IV: HÌNH HỌC TRỰC QUAN

BÀI 1:

HÌNH CHÓP TAM GIÁC ĐỀU

HỆ THỐNG KIẾN THỨC

1. Hình chóp tam giác đều

S

A

C

B

O

Hình S.ABC là một hình chóp tam giác đều. Có:

• S gọi là đỉnh.
• Mặt ABC là một tam giác đều được gọi là mặt đáy.
• Các đoạn thẳng SA,SB,SC bằng nhau và được gọi là các cạnh bên.

1. Hình chóp tam giác đều

S

A

C

B

O

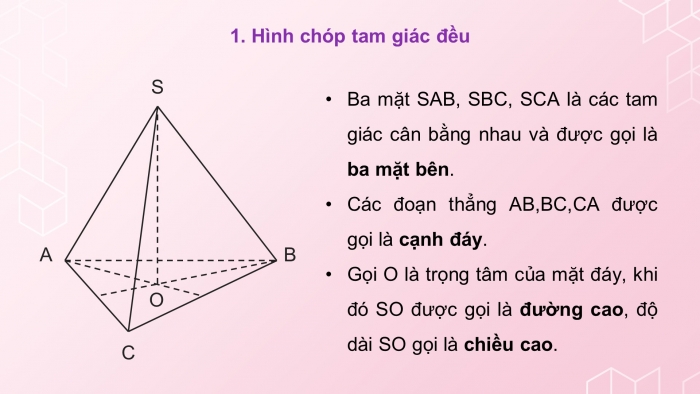
• Ba mặt SAB, SBC, SCA là các tam giác cân bằng nhau và được gọi là ba mặt bên.
• Các đoạn thẳng AB,BC,CA được gọi là cạnh đáy.
• Gọi O là trọng tâm của mặt đáy, khi đó SO được gọi là đường cao, độ dài SO gọi là chiều cao.

2. Diện tích xung quanh của hình chóp tam giác đều

Diện tích xung quanh của hình chóp tam giác đều bằng nửa tích của chu vi đáy với độ dài trung đoạn:

trong đó là diện tích xung quanh, là chu vi đáy, là độ dài trung đoạn của hình chóp tam giác đều.

3. Thể tích của hình chóp tam giác đều

Thể tích của hình chóp tam giác bằng một phần ba diện tích đáy với chiều cao.

( là thể tích, là diện tích đáy, là chiều cao)

LUYỆN TẬP

PHIẾU BÀI TẬP SỐ 1

DẠNG 1: Hình chóp tam giác đều

Phương pháp giải:

Áp dụng tính chất hình chóp tam giác đều có các cạnh đáy bằng nhau, các cạnh bên bằng nhau.

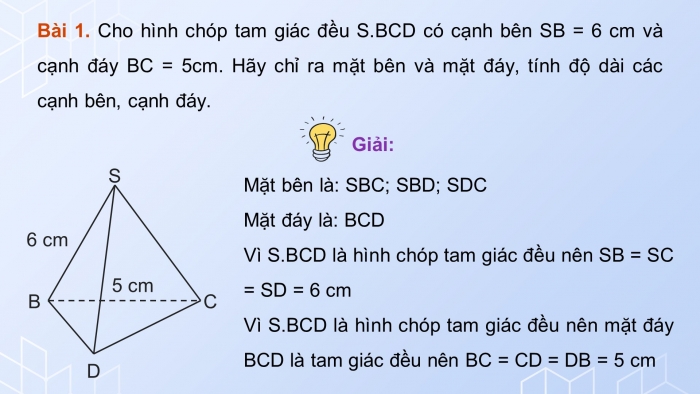
Bài 1. Cho hình chóp tam giác đều S.BCD có cạnh bên SB = 6 cm và cạnh đáy BC = 5cm. Hãy chỉ ra mặt bên và mặt đáy, tính độ dài các cạnh bên, cạnh đáy.

Giải:

S

B

D

C

6 cm

5 cm

Mặt bên là: SBC; SBD; SDC

Mặt đáy là: BCD

Vì S.BCD là hình chóp tam giác đều nên SB = SC = SD = 6 cm

Vì S.BCD là hình chóp tam giác đều nên mặt đáy BCD là tam giác đều nên BC = CD = DB = 5 cm

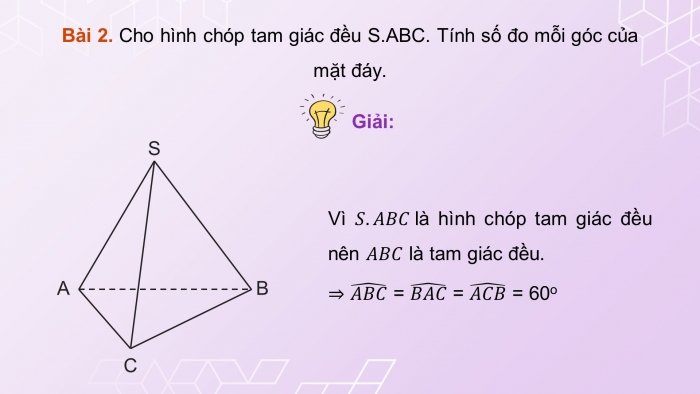
Bài 2. Cho hình chóp tam giác đều S.ABC. Tính số đo mỗi góc của mặt đáy.

Giải:

S

A

C

B

Vì là hình chóp tam giác đều nên là tam giác đều.

= = = 60o

Bài 3. Cho hình chóp tam giác đều S.BCD có cạnh bên SB = 4 cm và cạnh đáy BC = 3cm. Chu vi tam giác SBC.

Giải:

S

B

D

C

4 cm

3 cm

Vì S.BCD là hình chóp tam giác đều nên:

SB = SC = 5 cm

Chu vi tam giác SBC là:

SB + SC + BC = 4 + 4 + 3 = 11cm

Vì S.BCD là hình chóp tam giác đều nên ba mặt bên là các tam giác cân bằng nhau.

⇒ Chu vi ∆ SBC = chu vi ∆ SAB = 11 cm

Bài 4. Cho hình chóp tam giác đều S.BCD có cạnh bên SB = 4 cm và cạnh đáy BC = 3cm. Diện tích tam giác SBD.

Giải:

S

B

D

C

4 cm

3 cm

Vì là hình chóp tam giác đều nên cm

Chu vi tam giác là: cm

Nửa chu vi tam giác là cm

Diện tích tam giác là = cm2

Vì là hình chóp tam giác đều nên ba mặt bên là các tam giác cân bằng nhau.

Diện tích = diện tích = cm2

PHIẾU BÀI TẬP SỐ 2

DẠNG 2: Diện tích xung quanh và thể tích của hình chóp tam giác đều

Phương pháp giải:

Áp dụng tính chất diện tích xung quanh, diện tích toàn phần và thể tích của hình chóp tam giác đều.

Bài 1. Cho hình chóp tam giác đều có độ dài cạnh đáy là 4cm, chiều cao của hình chóp là 6 cm. Tính thể tích của hình chóp là?

Giải:

6 cm

4 cm

Do đáy là tam giác đều nên diện tích đáy là:

Vậy thể tích của hình chóp là:

Bài 2. Cho hình chóp tam giác đều cạnh 5cm và độ dài trung đoạn là 6cm. Tính diện tích xung quanh của hình chóp?

Giải:

6 cm

5 cm

Nửa chu vi của đáy ABC là (cm)

Áp dụng công thức diện tích xung quanh của hình chop:

Bài 3. Cho hình chóp tam giác đều , diện tích SBC bằng cm, chiều cao của tam giác mặt bên kẻ từ đỉnh của hình chóp tam giác đều cm, chiều cao của hình chóp là cm. Tính thể tích của hình chóp, biết chiều cao tam giác đáy bằng cm.

Giải:

S

B

C

A

cm

4 cm

---------------------------------------

----------------------Còn tiếp---------------------