Giáo án powerpoint dạy thêm Toán 8 cánh diều Chương 8 Bài tập cuối chương

CHÀO MỪNG CẢ LỚP  

ĐẾN VỚI TIẾT HỌC HÔM NAY! 

BÀI TẬP CUỐI CHƯƠNG VIII 

PHIẾU BÀI TẬP SỐ 1 

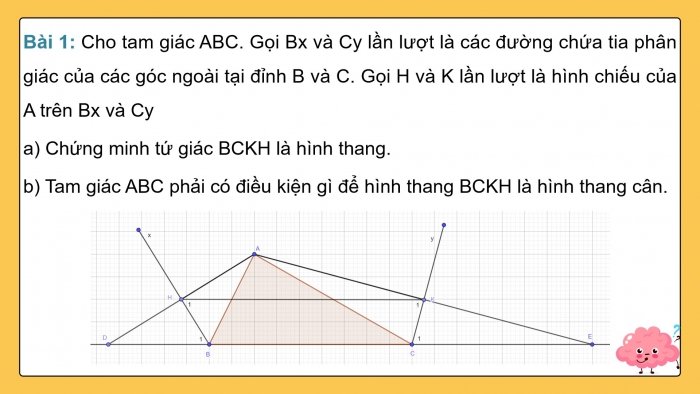
Bài 1: Cho tam giác ABC. Gọi Bx và Cy lần lượt là các đường chứa tia phân giác của các góc ngoài tại đỉnh B và C. Gọi H và K lần lượt là hình chiếu của A trên Bx và Cy 

1. a) Chứng minh tứ giác BCKH là hình thang.
2. b) Tam giác ABC phải có điều kiện gì để hình thang BCKH là hình thang cân.

Giải: 

1. a) Gọi D và E lần lượt là giao điểm của AH và AK với đường thẳng BC

∆ABD có BH vừa là phân giác, vừa là đường cao nên là tam giác cân ⇒ HA = HD 

Tương tự, ta có: KA = KE 

Xét ∆ADE có HK là đường trung bình nên HK // DE ⇒ HK // BC 

1. b) Ta có : (H_1) ̂=(B_1) ̂;(K_1) ̂=(C_1) ̂ (slt)

Hình thang BCKH là hình thang cân⇒(H_1) ̂=(K_1) ̂=>(B_1) ̂=(C_1) ̂ 

⇒(ABD) ̂=(ACE) ̂⇒(ABC) ̂=(ACB) ̂⇒∆ABC cân tại A 

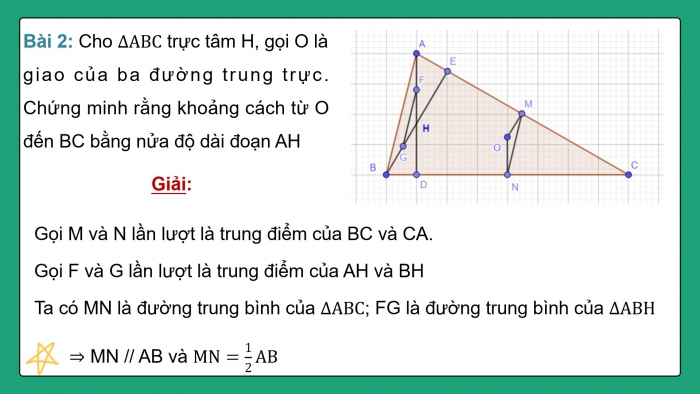
Bài 2: Cho ∆ABC trực tâm H, gọi O là giao của ba đường trung trực. Chứng minh rằng khoảng cách từ O đến BC bằng nửa độ dài đoạn AH 

Giải: 

Gọi M và N lần lượt là trung điểm của BC và CA. 

Gọi F và G lần lượt là trung điểm của AH và BH 

Ta có MN là đường trung bình của ∆ABC; FG là đường trung bình của ∆ABH 

⇒ MN // AB và MN=1/2AB 

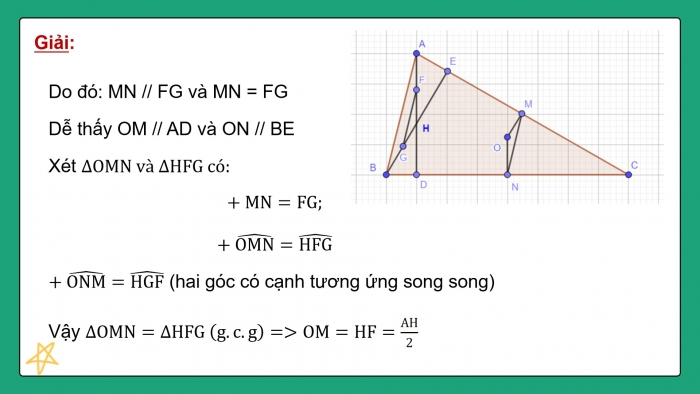
Do đó: MN // FG và MN = FG 

Dễ thấy OM // AD và ON // BE 

Xét ∆OMN và ∆HFG có: 

+ MN=FG; 

+ (OMN) ̂=(HFG) ̂ 

+ (ONM) ̂=(HGF) ̂ (hai góc có cạnh tương ứng song song) 

Vậy ∆OMN=∆HFG (g.c.g)=>OM=HF=AH/2 

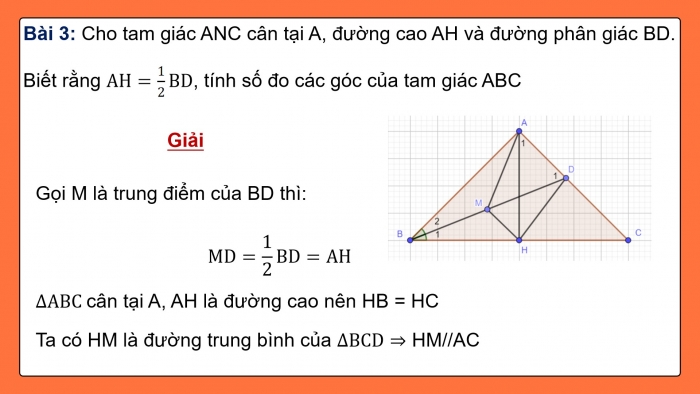
Bài 3: Cho tam giác ANC cân tại A, đường cao AH và đường phân giác BD. Biết rằng AH=1/2BD, tính số đo các góc của tam giác ABC 

Giải 

Gọi M là trung điểm của BD thì: 

MD=1/2BD=AH 

∆ABC cân tại A, AH là đường cao nên HB = HC 

Ta có HM là đường trung bình của ∆BCD ⇒ HM//AC 

Bài 4: Cho đoạn thẳng AB và n điểm O_1, O_2,…, O_n không nằm giữa A và B sao cho O_1A+O_2A+…+O_nA=O_1B+O_2B+…+O_nB=a. Chứng minh rằng tồn tại một điểm M sao cho O_1M+O_2M+…+O_nM≤a 

Giải 

* Trường hợp 1: 

O nằm trên tia đối của tia AB hay tia đối của tia BA, ta chứng minh được : 

OM=OA+OB/2 (1) 

* Trường hợp 2: Trường hợp O không thẳng hàng với A và B 

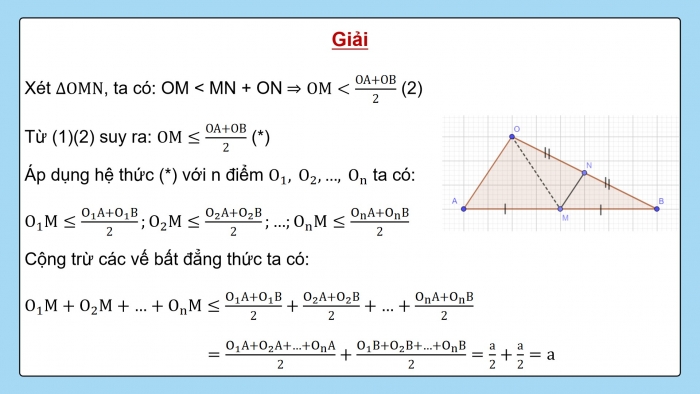
Gọi N là trung điểm của OB, khi đó MN là đường trung bình của ∆OAB 

MN=OA/2 

Xét ∆OMN, ta có: OM < MN + ON ⇒OM<OA+OB/2 (2) 

Từ (1)(2) suy ra: OM≤OA+OB/2 (*) 

Áp dụng hệ thức (*) với n điểm O_1, O_2,…, O_n ta có: 

O_1M≤O_1A+O_1B/2;O_2M≤O_2A+O_2B/2;…;O_nM≤O_nA+O_nB/2  

Cộng trừ các vế bất đẳng thức ta có: 

O_1M+O_2M+…+O_nM≤O_1A+O_1B/2+O_2A+O_2B/2+…+O_nA+O_nB/2  

  =O_1A+O_2A+…+O_nA/2+O_1B+O_2B+…+O_nB/2=a/2+a/2=a 

PHIẾU BÀI TẬP SỐ 2 

Bài 1: Cho hình vẽ 

1. a) ∆ABC có đồng dạng với ∆DEF hay không?
2. b) Tính tỉ số chu vi của hai tam giác

Giải: 

1. a) ta có: AB/DF=AC/DE=BC/EF=3/2→∆ABC∽∆DEF (c.c)
2. b) Có: ∆ABC∽∆DEF (c.c)→P_∆ABC/P_∆DEF=AB+BC+CA/DE+EF+FD=6+9+12/4+6+8=27/18=3/2

Bài 2: Cho tam giác ABC có độ dài các cạnh tỉ lệ với 4, 5, 6. Cho biết: ∆DFE đồng dạng với ∆ACB và cạnh nhỏ nhất của ∆DEF là 0,8cm. Tính độ dài các cạnh còn lại của ∆DEF 

Giải: 

Vì ∆DEF∽∆ABC nên ∆DEF cũng có độ dài cạnh tỉ lệ với 4, 5, 6 

Giả sử DE < EF < DF ⇒ DE = 0,8cm 

Vì ba cạnh của tam giác ABC có độ dài tỉ lệ với 4, 5, 6 nên ta có:  

DE/4=EF/5=FD/6=0,2⇒EF=1(cm);FD=1,2 cm 

Bài 3: Cho tam giác ABC đồng dạng với tam giác A’B’C’. Cho biết AB = 6cm, BC = 10cm, CA = 14cm và chu vi ∆A′B′C′ bằng 45cm. Tính độ dài các cạnh của tam giác A’B’C’. 

Giải 

Ta có: ∆ABC∾∆A^′B^′C^′→AB/A^′B^′=BC/B^′C^′=CA/C^′A^′=AB+BC+CA/A^′B^′+B^′C^′+C^′A^′=2/3 

⇒ A’B’ = 9cm; B’C’ = 15cm; A’C’ = 21cm 

Bài 4: Cho tứ giác ABCD có AB = 3cm, BC = 10cm, CD = 12cm, AD = 5cm, đường chéo BD = 6cm. Chứng minh: 

1. a) ∆ABD∾∆BCD
2. b) ABCD là hình thang

Giải 

1. a) Ta có: AB/BD=AD/BC=BD/DC=3/6=5/10=6/12→∆ABD∾∆BCD (c.c)
2. b) Vì ∆ABD∾∆BCD→(ABD) ̂=(BDC) ̂→AB//CD

⇒ ABCD là hình thang 

Bài 5: Cho tam giác ABC. Các đường cao AF, BK, CL cắt nhau tại H. Từ A kẻ Ax vuông góc với AB, từ C kẻ Cy vuông góc với BC. Gọi P là giao điểm của Ax và Cy. 

1. a) Chứng minh tứ giác AHCP là hình bình hành
2. b) Lấy O là trung điểm của BP. D, E lần lượt là trung điểm của BC và AC. Chứng minh: ∆ODE∾∆HAB

...