Giáo án điện tử toán 10 chân trời bài: Bài tập cuối chương IV

CHÀO MỪNG CÁC EM ĐẾN VỚI TIẾT HỌC HÔM NAY!
BÀI TẬP CUỐI CHƯƠNG IV
BÀI TẬP TRẮC NGHIỆM
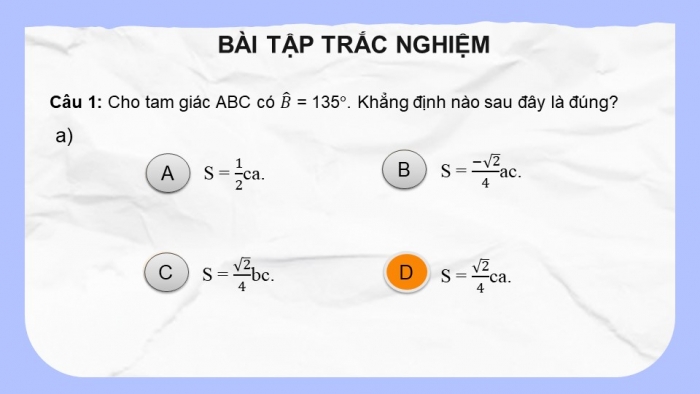
Câu 1: Cho tam giác ABC có B ̂ = 135°. Khẳng định nào sau đây là đúng?
S = 1/2ca.
S = 1/2ca.
S = √2/4bc.
S = √2/4ca.
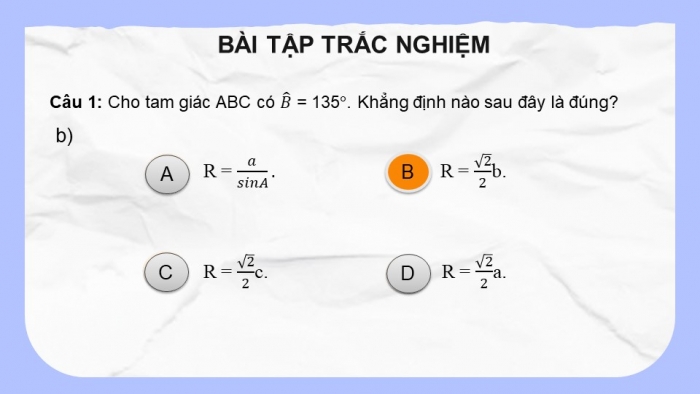
Câu 1: Cho tam giác ABC có B ̂ = 135°. Khẳng định nào sau đây là đúng?
R = a/sinA.
R = √2/2b.
R = √2/2c.
R = √2/2a.
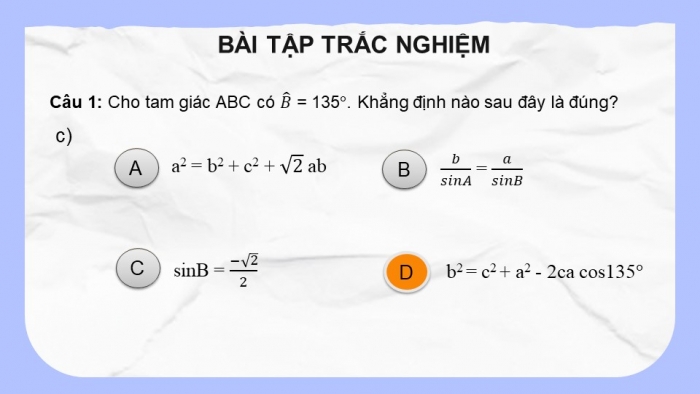
Câu 1: Cho tam giác ABC có B ̂ = 135°. Khẳng định nào sau đây là đúng?
a2 = b2 + c2 + √2 ab
b/sinA = a/sinB
sinB = (-√2)/2
b2 = c2 + a2 - 2ca cos135°
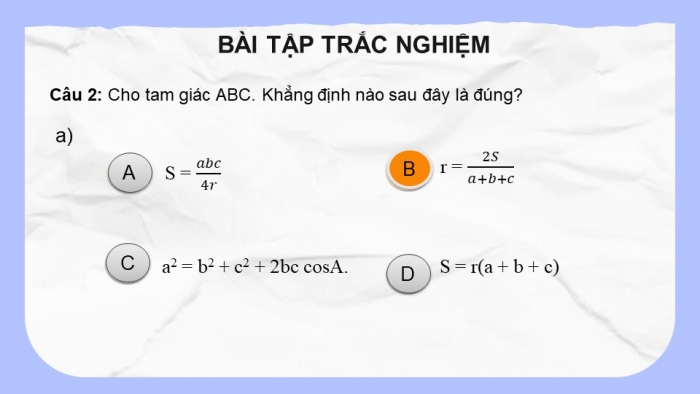
Câu 2: Cho tam giác ABC. Khẳng định nào sau đây là đúng?
S = abc/4r
r = 2S/(a+b+c)
a2 = b2 + c2 + 2bc cosA.
S = r(a + b + c)
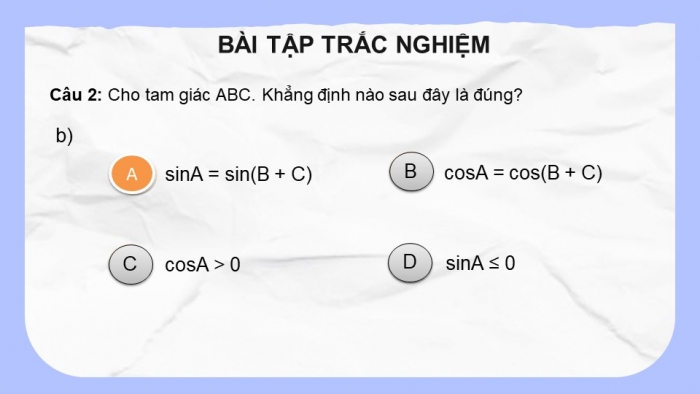
Câu 2: Cho tam giác ABC. Khẳng định nào sau đây là đúng?

sinA = sin(B + C)
cosA = cos(B + C)
cosA > 0
sinA ≤ 0
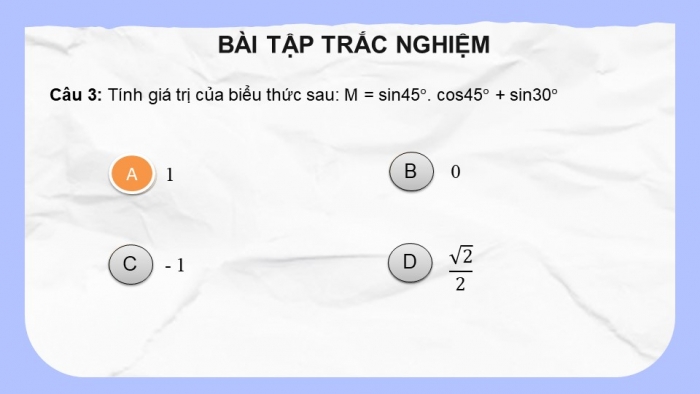
Câu 3: Tính giá trị của biểu thức sau: M = sin45°. cos45° + sin30°
1
0
-1
√2/2
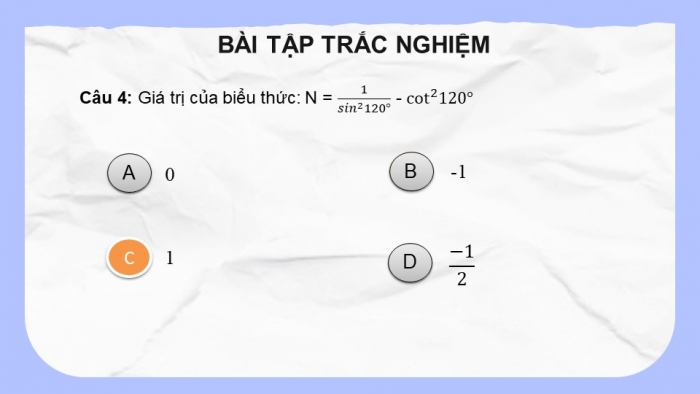
Câu 4: Giá trị của biểu thức: N = 1/(〖sin〗^2 120°) - cot^2 120°
0
-1
1
(-1)/2
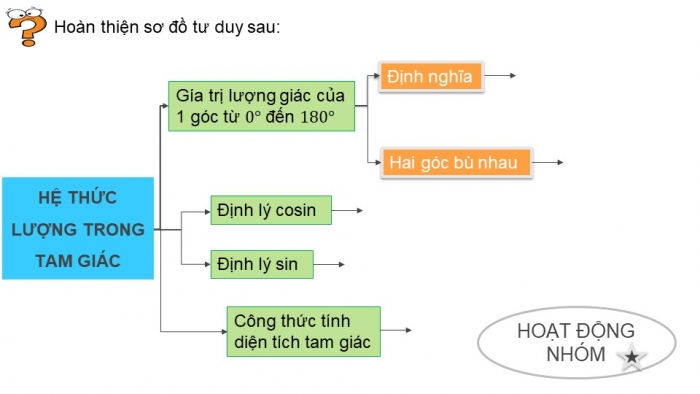
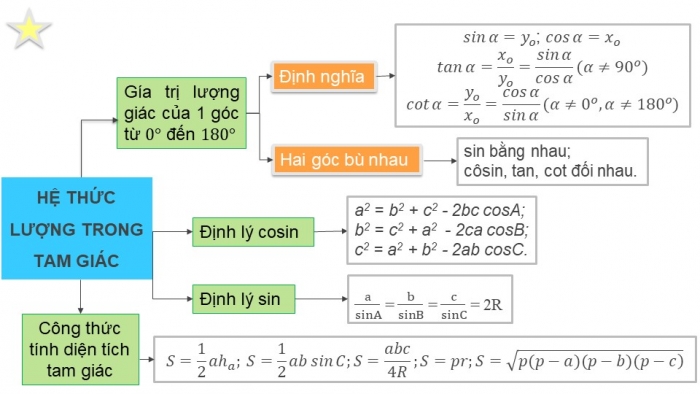
Hoàn thiện sơ đồ tư duy sau:
Bài 1 (SGK – tr78)
Cho tam giác ABC biết a = 49; b = 26,4; C ̂ = 47∘20'. Tính hai góc A ̂,B ̂ và cạnh c.
Giải
Áp dụng định lí côsin, ta có: c = √(a^2+b^2-2abcosC)
= √(〖49,4〗^2+〖26,4〗^2-2. 49,4.6,4cos47°20') ≈ 37
Áp dụng định lí sin, ta có : a/sinA = c/sinC
⟹ sinA = (a.sinC)/c = (49,4.sin47°20')/37 ≈ 0,982 ⟹ A ̂ ≈ 79°7’
⟹ B ̂ = 180° - A ̂ - C ̂ ≈ 180° - 79°7’ - 47°20’ = 53°33’
Bài 2 (SGK – tr78)
Cho tam giác ABC. Biết a = 24, b = 13, c = 15. Tính các góc A ̂,B ̂,C ̂
Giải
Áp dụng hệ quả của định lí côsin, ta có:
cosA = (b^2+c^2-a^2)/2bc = (13^2+15^2-24^2)/(2. 13. 15) = (-7)/15 ⟹ A ̂ ≈ 117°49’
Áp dụng định lí sin, ta có: a/sinA = b/sinB
⟹ sinB = (b.sinA)/a = (13.sin117°49')/24 ≈ 0,48 ⟹ B ̂ ≈ 28°41’
⟹ C ̂ = 180° - A ̂ - B ̂ ≈ 180° - 117°49’ - 28°41’ = 33°30’
Bài 3 (SGK – tr78)
Cho tam giác ABC có a = 8, b = 10, c = 13.
a. Tam giác ABC có góc tù không?
b. Tính độ dài trung tuyến AM, diện tích tam giác và bán kính dường tròn ngoại tiếp tam giác đó.
c. Lấy điểm D đối xứng với A qua C. Tính độ dài BD.
Giải
a. Ta có: cosC = (a^2+b^2-c^2)/2ab = (-1)/32 < 0 suy ra góc C tù.
b. Có: MC = MB = BC/2 = 8/2 = 4.
Áp dụng định lí côsin trong tam giác AMC, ta có :
AM2 = CA2 + CM2 - 2CA. CM. cos(ACM) ̂ = 102 + 42 - 2. 10. 4. (-1)/32 = 237/2
⟹ AM = √474/2
p = (a+b+c)/2 = 31/2 ;
S = √(p(p-a)(p-b)(p-c)) ≈ 39,98.
S = abc/4R ⟹ R = abc/4S ≈ 6,5
Bài 4 (SGK – tr79)
Cạnh a và các góc B ̂,C ̂.
b) Diện tích tam giác ABC;
c) Bán kính đường tròn ngoại tiếp và đường cao AH của tam giác.
Giải
a) Áp dụng định lí côsin, ta có: a2 = b2 + c2 - 2bc cosA ⟹ a = √129
Áp dụng định lí sin, ta có:
BC/sinA = AC/sinB ⟹ sinB = (4√43)/43 ⟹ B ̂ ≈ 37°35’
Vì A ̂ + B ̂ + C ̂ = 180°, suy ra C ̂ ≈ 22°25’.
b) S = 1/2bcsinA = 10√3.
c) S = abc/4R ⟹ R = abc/4S = √43 ; S = 1/2 a.ha ⟹ ha = 2S/a = (20√43)/43
Bài 6 (SGK – tr79)
Cho tam giác ABC có a = 15, b = 20, c = 25.
a) Tính diện tích tam giác ABC.
b) Tính bán kính đường tròn ngoại tiếp tam giác ABC.
Giải
a) Nửa chu vi của tam giác ABC là: p = (15+20+25)/2 = 30.
Vậy S = √(30(30-15)(30-20)(30-25)) = 150.
b) Ta có: S = abc/4R ⟹ R = abc/4S = 15.20.25/4.150 = 12,5.
Bài 5 (SGK – tr79)
Giải
a) Áp dụng định lí côsin, ta có:
AC2 = BA2 + BC2 - 2BC.BA.cosB
BD2 = BC2 + DC2 - 2BC. DC. cosC
= BC2 + AB2 + 2BC. AB. cosB
(vì DC = AB, cosC = -cosB).
Suy ra AC2 + BD2 = 2(AB2 + BC2).
b) Ta có: AC2 = 2(AB2 + BC2) - BD2 = 33.
Suy ra AC ≈ 5,7.
Bài 7 (SGK – tr79)
Giải
Ta có: cosA = (b^2+c^2-a^2)/2bc; sinA = a/2R
⇒ cotA = cosA/sinA = (R(b^2+c^2-a^2))/abc
Tương tự ta có: cotB = (R(a^2+c^2-b^2))/abc; cotC = (R(a^2+b^2-c^2))/abc
Suy ra: cotA + cotB + cotC = (R(a^2+b^2+c^2))/abc
VẬN DỤNG
Bài 8 (SGK – tr79)
Tính khoảng cách AB giữa hai nóc tòa cao ốc. Cho biết khoảng cách từ hai điểm đó đến một vệ tinh viễn thông lần lượt là 370 km, 350 km và góc nhìn từ vệ tinh đến A và B là 2,1°.

Giải
Gọi C là vị trí của vệ tinh.
Áp dụng định lí côsin trong tam giác ABC, ta có:
AB2 = CA2 + CB2 - 2CA. CB. cosC
= 3702 + 3502 - 2. 370. 350. cos(2,1°)
≈ 574
⟹ AB ≈ 24 (km).
Bài 9 (SGK – tr79)
Hai chiếc tàu thủy P và Q cách nhau 300 m và thẳng hàng với chân B của tháp hải đăng AB ở trên bờ biển. Từ P và Q, người ta nhìn thấy tháp hải đăng AB dưới các góc (BPA) ̂=35° và (BQA) ̂=48°. Tính chiều cao của tháp hải đăng đó.
Giải
Ta có: (BPA) ̂ = 35°, (BQA) ̂ = 48°, (ABP) ̂ = 90°, PQ = 300 ⟹ (AQP) ̂ = 132°, (PAQ) ̂ = 13°.
Áp dụng định lí sin trong tam giác APQ, ta có:
PQ/(sin(PAQ) ̂ ) = AQ/(sin(BPA) ̂ ) ⇒ AQ = (300.sin35°)/(sin13°) ≈ 765 (m)
Suy ra AB = AQ.sin48° ≈ 765. sin48° ≈ 569 (m).
Bài 10 (SGK – tr79)
Muốn đo chiều cao của một ngọn tháp, người ta lấy hai điểm A, B trên mặt đất có khoảng cách AB = 12 m cùng thẳng hàng với chân C của tháp để đặt hai giác kế. Chân của hai giác kế có chiều cao là h = 1,2 m. Gọi D là đỉnh tháp và hai điểm A1, B1 cùng thẳng hàng với C1 thuộc chiều cao CD của tháp. Người ta đo được (DA_1 C_1 ) ̂=49°, (DB_1 C_1 ) ̂=35°ˆ. Tính chiều cao CD của tháp.
Giải
Ta có: (B_1 A_1 D) ̂ = 180° - 49° = 131°,
(A_1 〖DB〗_1 ) ̂ = 180° - 35° - 131° = 14°.
Áp dụng định lí sin, ta có: (A_1 B_1)/(sin(A_1 DB_2 ) ̂ ) = (DA_1)/(sin(A_1 B_1 D) ̂ )
⟹ DA1 ≈ 28,45 (m)
sin(DA_1 C_1 ) ̂ = 〖DC〗_1/(DA_1 ) ⟹ DC1 ≈ 21,47 (m)
CD = CC1 + DC1 = 1,2 + 21,47 = 22,67 (m)
HƯỚNG DẪN VỀ NHÀ
Ghi nhớ kiến thức trong bài.
Hoàn thành các bài tập trong SBT.
Chuẩn bị trước "Bài 1 - Khái niệm vectơ".
HẸN GẶP LẠI CÁC EM Ở TIẾT HỌC SAU!