Giáo án điện tử Toán 8 chân trời Chương 7 Bài 2: Đường trung bình của tam giác
Bài giảng điện tử Toán 8 chân trời sáng tạo. Giáo án powerpoint Chương 7 Bài 2: Đường trung bình của tam giác. Giáo án thiết kế theo phong cách hiện đại, nội dung đầy đủ, đẹp mắt, tạo hứng thú học tập cho học sinh. Thầy, cô giáo có thể tham khảo.
Xem: => Giáo án toán 8 chân trời sáng tạo
Click vào ảnh dưới đây để xem 1 phần giáo án rõ nét





Các tài liệu bổ trợ khác
Xem toàn bộ: Giáo án điện tử toán 8 chân trời sáng tạo
CHÀO MỪNG CÁC EM
ĐẾN VỚI TIẾT HỌC HÔM NAY!
KHỞI ĐỘNG
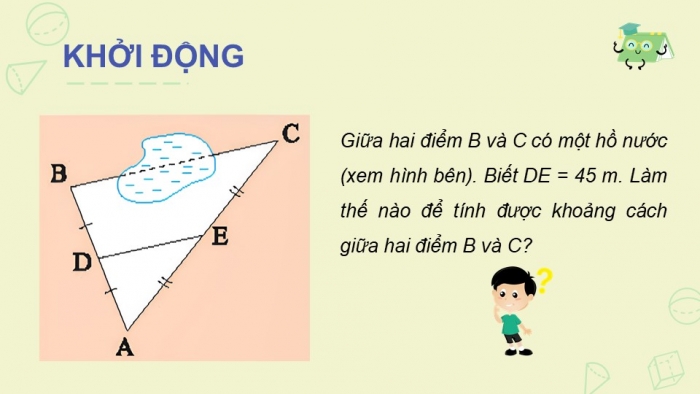
Giữa hai điểm B và C có một hồ nước (xem hình bên). Biết DE = 45 m. Làm thế nào để tính được khoảng cách giữa hai điểm B và C?
BÀI 2: ĐƯỜNG TRUNG BÌNH CỦA TAM GIÁC
NỘI DUNG BÀI HỌC
ĐƯỜNG TRUNG BÌNH CỦA TAM GIÁC
TÍNH CHẤT CỦA ĐƯỜNG TRUNG BÌNH
- ĐƯỜNG TRUNG BÌNH CỦA TAM GIÁC
HĐKP1
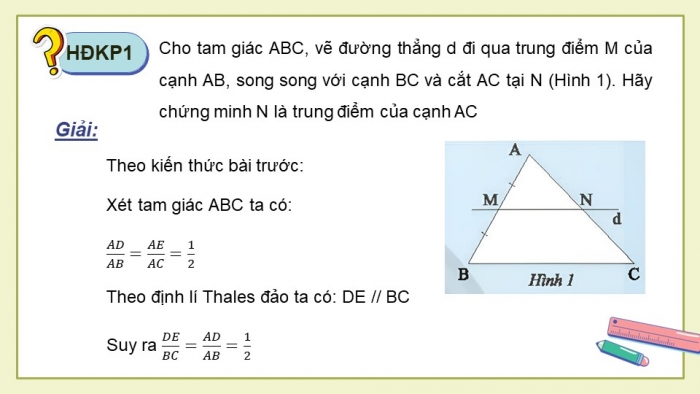
Cho tam giác ABC, vẽ đường thẳng d đi qua trung điểm M của cạnh AB, song song với cạnh BC và cắt AC tại N (Hình 1). Hãy chứng minh N là trung điểm của cạnh AC
Giải:
Theo kiến thức bài trước:
Xét tam giác ABC ta có:
Theo định lí Thales đảo ta có: DE // BC
Suy ra
Cho tam giác ABC, vẽ đường thẳng d đi qua trung điểm M của cạnh AB, song song với cạnh BC và cắt AC tại N (Hình 1). Hãy chứng minh N là trung điểm của cạnh AC
Giải:
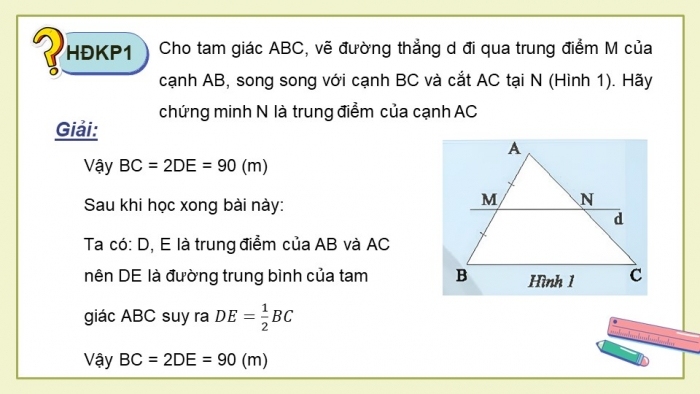
Vậy BC = 2DE = 90 (m)
Sau khi học xong bài này:
Ta có: D, E là trung điểm của AB và AC nên DE là đường trung bình của tam giác ABC suy ra
Vậy BC = 2DE = 90 (m)
Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba.
Định nghĩa
Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
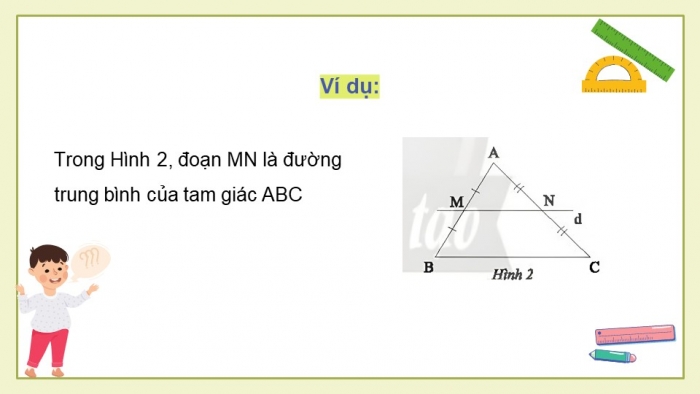
Ví dụ:
Trong Hình 2, đoạn MN là đường trung bình của tam giác ABC
Ví dụ 1: Trong Hình 3, tìm các đường trung bình của tam giác XYZ
Giải:
Vì A, B lần lượt là trung điểm của XY và XZ nên AB là đường trung bình của tam giác XYZ. Tương tự, ta cũng có BC và CA là các đường trung bình của tam giác XYZ
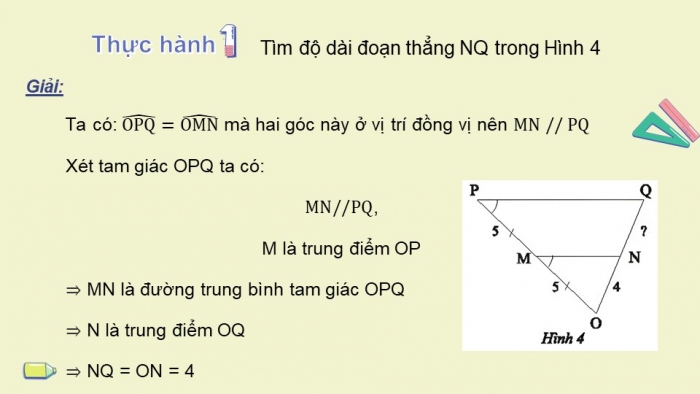
Tìm độ dài đoạn thẳng NQ trong Hình 4
Giải:
Ta có: mà hai góc này ở vị trí đồng vị nên
Xét tam giác OPQ ta có:
,
M là trung điểm OP
⇒ MN là đường trung bình tam giác OPQ
⇒ N là trung điểm OQ
⇒ NQ = ON = 4
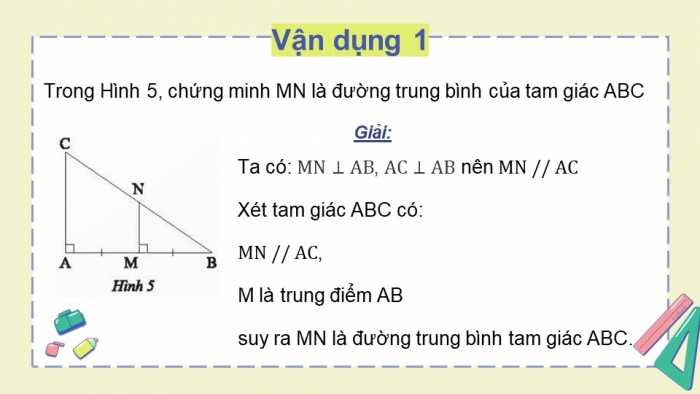
Vận dụng 1
Trong Hình 5, chứng minh MN là đường trung bình của tam giác ABC
Giải:
Ta có: , nên
Xét tam giác ABC có:
,
M là trung điểm AB
suy ra MN là đường trung bình tam giác ABC.
- TÍNH CHẤT CỦA ĐƯỜNG TRUNG BÌNH
Cho M, N lần lượt là trung điểm của hai cạnh AB và AC của tam giác ABC
- a) Tính các tỉ số ,
- b) Chứng minh MN // BC
- c) Chứng minh
Giải:
- a) Vì M là trung điểm AB suy ra
Tương tự,
- b) Xét tam giác ABC có:
Theo định lí Thalès đảo ta có: MN // BC
- c) Xét tam giác ABC có MN // BC
Áp dụng hệ quả của định lí Thalès, ta có:
Trên chỉ là 1 phần của giáo án. Giáo án khi tải về có đầy đủ nội dung của bài. Đủ nội dung của học kì I + học kì II
Đủ kho tài liệu môn học
=> Tài liệu sẽ được gửi ngay và luôn
Cách tải:
- Bước 1: Chuyển phí vào STK: 1214136868686 - cty Fidutech - MB
- Bước 2: Nhắn tin tới Zalo Fidutech - nhấn vào đây để thông báo và nhận tài liệu
Xem toàn bộ: Giáo án điện tử toán 8 chân trời sáng tạo
ĐẦY ĐỦ GIÁO ÁN CÁC BỘ SÁCH KHÁC
GIÁO ÁN WORD LỚP 8 CHÂN TRỜI SÁNG TẠO
GIÁO ÁN POWERPOINT LỚP 8 CHÂN TRỜI SÁNG TẠO
GIÁO ÁN DẠY THÊM LỚP 8 CHÂN TRỜI SÁNG TẠO
CÁCH ĐẶT MUA:
Liên hệ Zalo: Fidutech - nhấn vào đây
