Giáo án và PPT Toán 8 chân trời Bài 5: Hình chữ nhật – Hình vuông
Đồng bộ giáo án word và powerpoint (ppt) Bài 5: Hình chữ nhật – Hình vuông. Thuộc chương trình Toán 8 chân trời sáng tạo. Giáo án được biên soạn chỉnh chu, hấp dẫn. Nhằm tạo sự lôi cuốn và hứng thú học tập cho học sinh.
Click vào ảnh dưới đây để xem giáo án WORD rõ nét












Giáo án ppt đồng bộ với word








Còn nữa....
Các tài liệu bổ trợ khác
Xem toàn bộ: Trọn bộ giáo án và PPT Toán 8 chân trời sáng tạo
CHƯƠNG 3. ĐỊNH LÝ PYTHAGORE. CÁC LOẠI TỨ GIÁC THƯỜNG GẶP
BÀI 5. HÌNH CHỮ NHẬT – HÌNH VUÔNG
HOẠT ĐỘNG KHỞI ĐỘNG
GV yêu cầu HS thảo luận và trả lời:
Cho hình thang cân ABCD, đáy nhỏ AB = 6, CD = 18, AD = 10.
Gọi I, K, M, L lần lượt là trung điểm của các đoạn BC, CA, AD và BD. Tứ giác ABKL là hình gì?
HOẠT ĐỘNG HÌNH THÀNH KIẾN THỨC
Hoạt động 1. Hình chữ nhật
GV đặt câu hỏi hướng dẫn học sinh tìm hiểu: Hình chữ nhật là ?
Sản phẩm dự kiến:
HĐ1
Định nghĩa
HĐKP1:

Dùng thước đo góc ta xác định được:
![]()
Nhận xét: ![]()
![]() Kết luận:
Kết luận:
Hình chữ nhật là tứ giác có bốn góc vuông.
Ví dụ 1: (SGK – tr82)
- Tính chất:
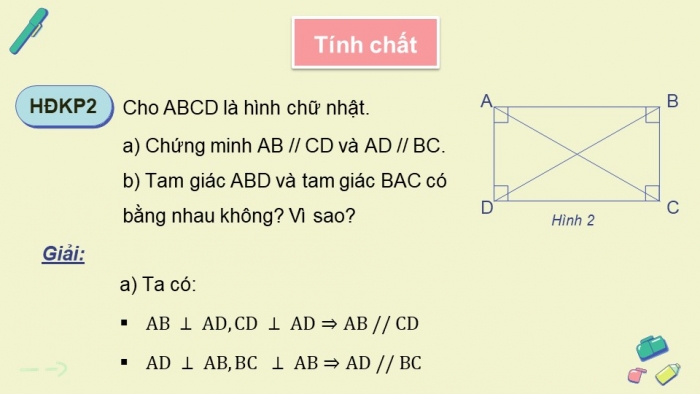
HĐKP2

a) Ta có:
+ ![]()
![]()
+ ![]()
![]()
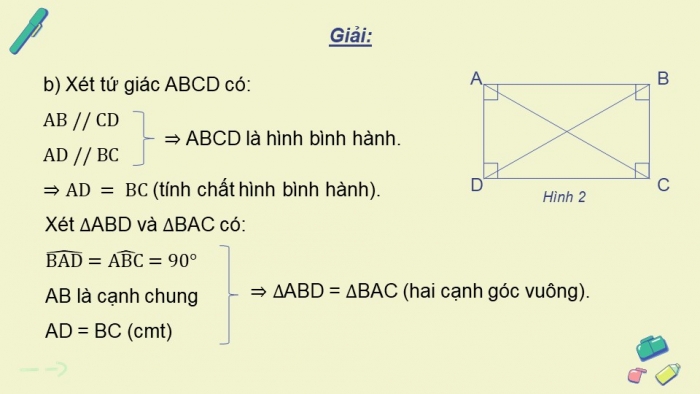
b) Xét tứ giác ABCD có:
![]()
![]()
![]() ABCD là hình bình hành.
ABCD là hình bình hành.
![]() (tính chất hình bình hành).
(tính chất hình bình hành).
Xét ![]() ABD và
ABD và ![]() BAC có:
BAC có:
![]()
AB là cạnh chung;
AD = BC (cmt)
Do đó ![]() ABD =
ABD = ![]() BAC (hai cạnh góc vuông).
BAC (hai cạnh góc vuông).
Chú ý:
Hình chữ nhật cũng là hình thang cân và cũng là hình bình hành.
![]() Kết luận:
Kết luận:
Trong hình chữ nhật, hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.
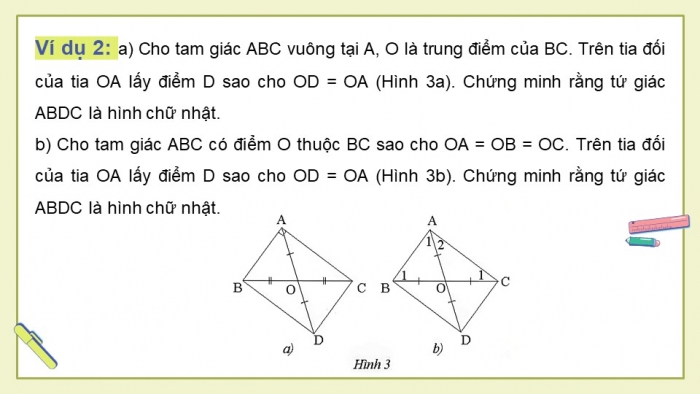
Ví dụ 2: (SGK – tr83)
Chú ý:
- Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền thì bằng nửa cạnh huyền.
- Nếu một tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh ấy thì tam giác đó là tam giác vuông.
Thực hành 1:
| a | 8 |
| 12 |
| b | 6 |
| 5 |
| d | 10 |
| 13 |
Vận dụng 1.
Bốn ví dụ về hình chữ nhật trong thực tế: mặt bảng viết; mặt bìa quyển vở; màn hình ti vi, mặt tủ lạnh,…
- Dấu hiệu nhận biết
HĐKP3

a)
Do ABCD là hình bình hành
![]()
Do ![]() là góc vuông
là góc vuông ![]()
Có:
+) ![]()
Hay ![]() là góc vuông.
là góc vuông.
+) ![]()
Hay ![]() là góc vuông.
là góc vuông.
b) Xét hình bình hành ABCD có:
AB // CD
![]() ABCD cũng là hình thang có hai cạnh đáy là AB và CD.
ABCD cũng là hình thang có hai cạnh đáy là AB và CD.
Lại có hai đường chéo AC = BD
![]() ABCD là hình thang cân.
ABCD là hình thang cân.
Do đó: ![]()
Tương tự ta cũng có: ![]()
![]()
![]()
Mà: ![]()
Hay ![]() , do đó
, do đó ![]()
![]() Kết luận:
Kết luận:
Ta có dấu hiệu nhận biết một tứ giác là hình chữ nhật như sau:
1. Hình bình hành có một góc vuông là hình chữ nhật.
2. Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.
Chú ý:
- Tứ giác có ba góc vuông là hình chữ nhật.
- Hình thang cân có một góc vuông là hình chữ nhật.
Ví dụ 3: (SGK – tr84)
Thực hành 2.
Gọi tứ giác đã cho là ABCD (hình vẽ).

+ Dùng compa kiểm tra được AB = CD; AD = BC và AC = BD.
+ Tứ giác ABCD có AB = CD và AD = BC nên là hình bình hành.
Lại có hai đường chéo AC = BD nên hình bình hành ABCD là hình chữ nhật.
Vận dụng 2.
a) Dùng êke ba lần ta đo ba góc:
![]() ta được
ta được ![]()
Xét tứ giác ABCD có:
![]()
![]() ABCD là hình chữ nhật.
ABCD là hình chữ nhật.
b) Sử dụng một cuộn dây:

+ Ta đo đoạn thẳng AB bằng cách đánh dấu 2 điểm trên đoạn dây sao cho hai điểm đánh dấu trùng với hai điểm A, B.
+ Đặt điểm đánh dấu thứ nhất trùng với điểm D và kiểm tra thấy điểm đánh dấu còn lại trùng với điểm C. Khi đó AB = CD.
+ Làm tương tự ta cũng xác định được AD = BC và AC = BD.
Tứ giác ABCD có AB = CD, AD = BC nên là hình bình hành.
Lại có hai đường chéo AC = BD nên hình bình hành ABCD là hình chữ nhật.
Hoạt động 2. Hình vuông
GV đưa ra câu hỏi: Hình vuông là?
Sản phẩm dự kiến:
Định nghĩa
HĐKP4.

+ Tứ giác ABCD có bốn cạnh bằng nhau nên là hình thoi.
+ Tứ giác ABCD có bốn góc bằng nhau nên ![]()
Mà ![]()
Hay ![]() , suy ra
, suy ra ![]() .
.
Do đó
![]()
![]() ABCD là hình chữ nhật.
ABCD là hình chữ nhật.
Vậy ABCD vừa là hình thoi vừa là hình chữ nhật.
![]() Kết luận:
Kết luận:
Hình vuông là tứ giác có bốn góc vuông và bốn cạnh bằng nhau.
Tính chất:
HĐKP5.

+ MNPQ là hình vuông nên là tứ giác có bốn góc vuông và bốn cạnh bằng nhau.
+ Hình vuông MNPQ có bốn góc vuông nên là hình chữ nhật.
+ Hình vuông MNPQ có bốn cạnh bằng nhau nên là hình thoi.
Vậy hình vuông MNPQ vừa là hình chữ nhật vừa là hình thoi.
Nhận xét:
Hình vuông có tất cả các tính chất của hình chữ nhật và hình thoi.
Ví dụ 4: SGK – tr85
Thực hành 3.

a)
Tứ giác MNPQ có hai đường chéo cắt nhau MP và NQ tại trung điểm O của mỗi đường nên là hình bình hành.
Lại có hai đường chéo MP và NQ vuông góc với nhau tại O nên hình bình hành MNPQ là hình thoi (1).
Mặt khác: ![]()
![]()
Mà ![]() nên
nên ![]() .
.
Ta có MNPQ là hình thoi nên cũng là hình bình hành.
Mà hai đường chéo MP và NQ bằng nhau nên hình bình hành MNPQ là hình chữ nhật (2)
Từ (1) và (2) suy ra MNPQ là hình vuông.
b)
Tứ giác RSTU có RS = ST = TU = UR nên là hình thoi (1)
Do đó RSTU cũng là hình bình hành.
Lại có ![]() nên hình bình hành RSTU là hình chữ nhật (2)
nên hình bình hành RSTU là hình chữ nhật (2)
Từ (1) và (2) suy ra RSTU là hình vuông.
Vậy hai hình MNPQ và RSTU đều là hình vuông
Vận dụng 3:
Bốn ví dụ về hình vuông trong thực tế:
Mặt bìa hộp bánh pizza, gạch lát nền, mặt xúc xắc, khung ảnh hình vuông,…
Dấu hiệu nhận biết
HĐKP6
+) Trường hợp 1: AB = BC.

Do ABCD là hình chữ nhật nên cũng là hình bình hành.
Lại có hai cạnh kề bằng nhau AB = BC nên hình bình hành ABCD là hình thoi.
ABCD vừa là hình chữ nhật vừa là hình thoi
![]() ABCD là hình vuông.
ABCD là hình vuông.
+) Trường hợp 2: AC vuông góc với BD.

Do ABCD là hình chữ nhật nên cũng là hình bình hành.
Lại có hai đường chéo vuông góc nên hình bình hành ABCD là hình thoi.
ABCD vừa là hình chữ nhật vừa là hình thoi
![]() ABCD là hình vuông.
ABCD là hình vuông.
+) Trường hợp 3: AC là đường phân giác của góc BAD.

Do ABCD là hình chữ nhật nên cũng là hình bình hành.
Lại có đường chéo AC là đường phân giác của góc BAD nên hình bình hành ABCD là hình thoi.
ABCD vừa là hình chữ nhật vừa là hình thoi
![]() ABCD là hình vuông.
ABCD là hình vuông.
HĐKP7.
a)

Ta có hình thoi ABCD cũng là hình bình hành.
Mà ![]() nên hình bình hành ABCD là hình chữ nhật.
nên hình bình hành ABCD là hình chữ nhật.
Do đó ![]()
b)

Ta có hình thoi ABCD cũng là hình bình hành.
Mà hai đường chéo AC = BD nên hình bình hành ABCD là hình chữ nhật.
Do đó ![]() .
.
![]() Kết luận:
Kết luận:
1. Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.
2. Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.
3. Hình chữ nhật có một đường chéo là đường phân giác của một góc là hình vuông.
* Chú ý:
- Hình thoi có một góc vuông là hình vuông.
- Hình thoi có hai đường chéo bằng nhau là hình vuông.
Ví dụ 5: SGK – tr86
Thực hành 4.

a) Do ABCD là một hình vuông nên ![]() và AB = BC = CD = DA.
và AB = BC = CD = DA.
Mà AE = BF = CG = DH nên EB = FC = GD = HA.
Xét ![]() AEH và
AEH và ![]() DGH có:
DGH có:
![]()
![]()
![]()
Do đó ![]() AEH =
AEH = ![]() DHG (hai cạnh góc vuông)
DHG (hai cạnh góc vuông)
Suy ra ![]() (hai góc tương ứng).
(hai góc tương ứng).
Xét ![]() AHE có:
AHE có:
![]() (trong tam giác vuông, tổng hai góc nhọn bằng 90°).
(trong tam giác vuông, tổng hai góc nhọn bằng 90°).
Do đó ![]()
Hay ![]()
![]()
Khi đó ![]() là một góc vuông.
là một góc vuông.
CMTT ta cũng có ![]() là một góc vuông.
là một góc vuông.
Vậy tứ giác EFGH có ba góc vuông.
b) Do ![]() AEH =
AEH = ![]() DHG (câu a)
DHG (câu a)
Suy ra HE = HG (hai cạnh tương ứng).
c) CMTT câu b, ta cũng có:
![]()
Xét tứ giác EFGH có:
![]()
![]() EFGH là hình thoi.
EFGH là hình thoi.
Tứ giác EFGH có ba góc vuông
![]() EFGH là hình chữ nhật.
EFGH là hình chữ nhật.
Tứ giác EFGH vừa là hình thoi vừa là hình chữ nhật nên là hình vuông.
Vận dụng 4:

Do mặt kính của chiếc đồng hồ để bàn có ba góc vuông nên mặt kính có dạng hình chữ nhật.
Mà mặt kính có hai cạnh kề bằng nhau nên mặt kính có dạng hình vuông.
HOẠT ĐỘNG LUYỆN TẬP
Từ nội dung bài học,GV yêu cầu HS luyện tập làm bài:
Câu 1: Hãy chọn câu trả lời đúng. Hình bình hành ABCD là hình chữ nhật khi:
- A. AB = BC
- B. AC = BD
- C. BC = CD
- D. AC⊥ BD
Câu 2: Cho tam giác ABC vuông tại A, điểm M thuộc cạnh huyền BC. Gọi D, E lần lượt là chân đường vuông góc kẻ từ M đến AB, AC. Tứ giác ADME là hình gì?
- A. Hình thang
- B. Hình chữ nhật
- C. Hình bình hành
- D. Hình vuông
Câu 3: Độ dài đường trung tuyến ứng với cạnh huyền của tam giác vuông có các cạnh góc vuông bằng 5cm, 12cm là:
- A. 6,5cm
- B. 6cm
- C. 13cm
- D. 10cm
Câu 4: Hãy chọn câu sai. Hình chữ nhật có
- A. Bốn góc
- B. Hai đường chéo giao nhau tại trung điểm mỗi đường
- C. Hai đường chéo vuông góc với nhau
- D. Các cạnh đối bằng nhau
Câu 5: Cho tam giác ABC vuông tại A, AC = 6cm, điểm M thuộc cạnh BC. Gọi D, E theo thứ tự là các chân đường vuông góc kẻ từ M đến AB, AC. Chu vi của tứ giác ADME bằng:
- A. 6cm
- B. 36cm
- C. 18cm
- D. 12cm
Sản phẩm dự kiến:
| Câu 1 - B | Câu 2 - B | Câu 3 -A | Câu 4 -C | Câu 5 -D |
HOẠT ĐỘNG VẬN DỤNG
Vận dụng kiến thức, GV yêu cầu HS trả lời câu hỏi:
Câu 1: Cho tam giác ABC vuông tại A, AC = 8cm, điểm M thuộc cạnh BC. Gọi D, E theo thứ tự là các chân đường vuông góc kẻ từ M đến AB, AC. Chu vi của tứ giác ADME bằng:
Câu 2: Cho hình chữ nhật ABCD có AB = a;AD = b. Cho M, N, P, Q là các đỉnh của tứ giác MNPQ và lần lượt thuộc các cạnh AB, BC, CD, DA. Tìm giá trị nhỏ nhất của chu vi tứ giác MNPQ.
Trên chỉ là 1 phần của giáo án. Giáo án khi tải về có đầy đủ nội dung của bài. Đủ nội dung của học kì I + học kì II
Đủ kho tài liệu môn học
=> Tài liệu sẽ được gửi ngay và luôn
Cách tải:
- Bước 1: Chuyển phí vào STK: 1214136868686 - cty Fidutech - MB
- Bước 2: Nhắn tin tới Zalo Fidutech - nhấn vào đây để thông báo và nhận tài liệu
Xem toàn bộ: Trọn bộ giáo án và PPT Toán 8 chân trời sáng tạo
TÀI LIỆU GIẢNG DẠY TOÁN 8 KẾT NỐI TRI THỨC
Giáo án toán 8 kết nối tri thức đủ cả năm
Giáo án điện tử toán 8 kết nối tri thức
Giáo án dạy thêm toán 8 kết nối tri thức đủ cả năm
Giáo án powerpoint dạy thêm toán 8 kết nối tri thức đủ cả năm
Trò chơi khởi động Toán 8 kết nối tri thức
Video AI khởi động Toán 8 kết nối tri thức hấp dẫn
Câu hỏi và bài tập trắc nghiệm toán 8 kết nối tri thức
Đề thi toán 8 kết nối tri thức
File word đáp án toán 8 kết nối tri thức
Bài tập file word toán 8 kết nối tri thức
Kiến thức trọng tâm Toán 8 kết nối tri thức
Đề kiểm tra 15 phút Toán 8 kết nối tri thức
Phiếu học tập theo bài Toán 8 kết nối tri thức cả năm
Trắc nghiệm dạng câu trả lời ngắn Toán 8 kết nối tri thức cả năm
Trắc nghiệm đúng sai Toán 8 kết nối tri thức cả năm
TÀI LIỆU GIẢNG DẠY TOÁN 8 CHÂN TRỜI SÁNG TẠO
Giáo án toán 8 chân trời sáng tạo đủ cả năm
Giáo án điện tử toán 8 chân trời sáng tạo
Giáo án dạy thêm toán 8 chân trời sáng tạo đủ cả năm
Giáo án powerpoint dạy thêm toán 8 chân trời sáng tạo đủ cả năm
Trò chơi khởi động Toán 8 chân trời sáng tạo
Video AI khởi động Toán 8 chân trời sáng tạo hấp dẫn
Câu hỏi và bài tập trắc nghiệm toán 8 chân trời sáng tạo
Đề thi toán 8 chân trời sáng tạo
File word đáp án toán 8 chân trời sáng tạo
Bài tập file word toán 8 chân trời sáng tạo
Kiến thức trọng tâm Toán 8 chân trời sáng tạo
Đề kiểm tra 15 phút Toán 8 chân trời sáng tạo
Phiếu học tập theo bài Toán 8 chân trời sáng tạo cả năm
Trắc nghiệm dạng câu trả lời ngắn Toán 8 chân trời sáng tạo cả năm
Trắc nghiệm đúng sai Toán 8 chân trời sáng tạo cả năm
TÀI LIỆU GIẢNG DẠY TOÁN 8 CÁNH DIỀU
Giáo án toán 8 cánh diều đủ cả năm
Giáo án điện tử toán 8 cánh diều
Giáo án dạy thêm toán 8 cánh diều đủ cả năm
Giáo án powerpoint dạy thêm toán 8 cánh diều đủ cả năm
Trò chơi khởi động Toán 8 cánh diều
Video AI khởi động Toán 8 cánh diều hấp dẫn
Câu hỏi và bài tập trắc nghiệm toán 8 cánh diều
Đề thi toán 8 cánh diều
File word đáp án toán 8 cánh diều
Bài tập file word toán 8 cánh diều
Kiến thức trọng tâm Toán 8 cánh diều
Đề kiểm tra 15 phút Toán 8 cánh diều
Phiếu học tập theo bài Toán 8 cánh diều cả năm
Trắc nghiệm dạng câu trả lời ngắn Toán 8 cánh diều cả năm
Trắc nghiệm đúng sai Toán 8 cánh diều cả năm
