Giáo án điện tử Toán 8 cánh diều Chương 5 Bài 4: Hình bình hành

CHÀO MỪNG CÁC EM ĐẾN VỚI BUỔI HỌC NGÀY HÔM NAY!

KHỞI ĐỘNG

Trong thiết kế tay vịn cầu thang (hình 34), người ta thường để các cặp thanh sườn song song với nhau, các cặp thanh trụ song song với nhau, tạo nên các hình bình hành.

Hình bình hành có những tính chất gì? Có những dấu hiệu nào để nhận biết một tứ giác là hình bình hành?

CHƯƠNG V. ĐỊNH LÍ PYTHAGORE. TỨ GIÁC

BÀI 4. HÌNH BÌNH HÀNH

NỘI DUNG BÀI HỌC

Định nghĩa

Tính chất

Dấu hiệu nhận biết

1. ĐỊNH NGHĨA

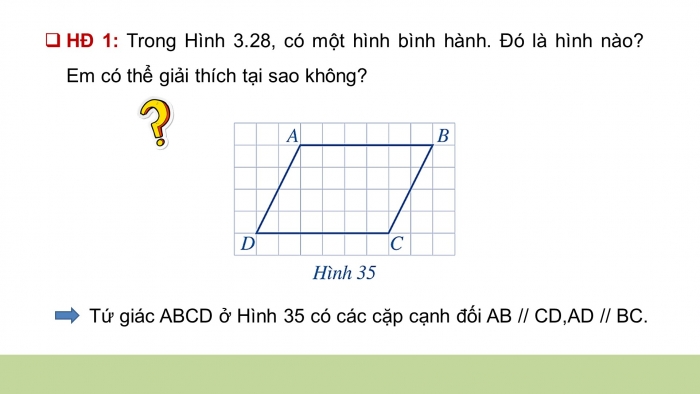
• HĐ 1: Trong Hình 3.28, có một hình bình hành. Đó là hình nào? Em có thể giải thích tại sao không?

> Tứ giác ABCD ở Hình 35 có các cặp cạnh đối AB // CD,AD // BC.

ĐỊNH NGHĨA

Hình bình hành là tứ giác có hai cặp cạnh đối song song.

Ví dụ 1

Ở Hình 36, tứ giác nào là hình bình hành? Vì sao?

Giải:

- Ở Hình 36a, ta có  và  ở vị trí đồng vị nên MN // PQ

Ta lại có , và  ở vị trí đồng vị nên  MQ // NP.

Do đó, tứ giác MNPQ là hình bình hành.

- Ở Hình 36b, AB và CD cắt nhau tại O nên AB và CD không song song với nhau. Do đó,          tứ giác ABDC không phải là hình bình hành.

2. TÍNH CHẤT

• HĐ 2: Cho hình bình hành ABCD (Hình 37).

1. a) Hai tam giác ABD và CDB có bằng nhau hay không? Từ đó, hãy so sánh các cặp đoạn thẳng: AB và CD; DA và BC.
2. b) So sánh các cặp góc: và ; và  
3. c) Hai tam giác OAB và OCD có bằng nhau hay không? Từ đó, hãy so sánh các cặp đoạn thẳng: OA và OC; OB và OD.

Giải:

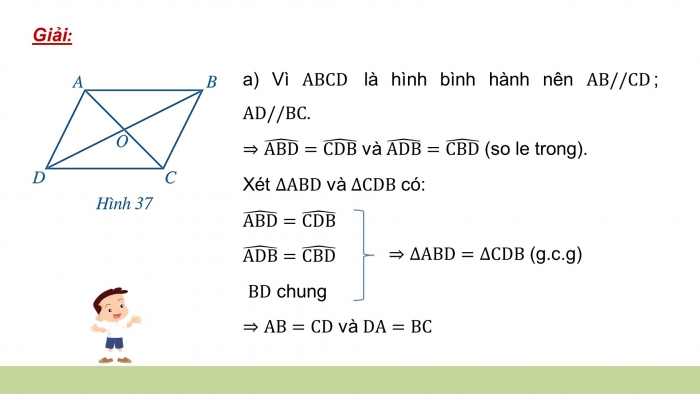
1. a) Vì là hình bình hành nên ; .

 và  (so le trong).

Xét  và  có:

  chung

  và

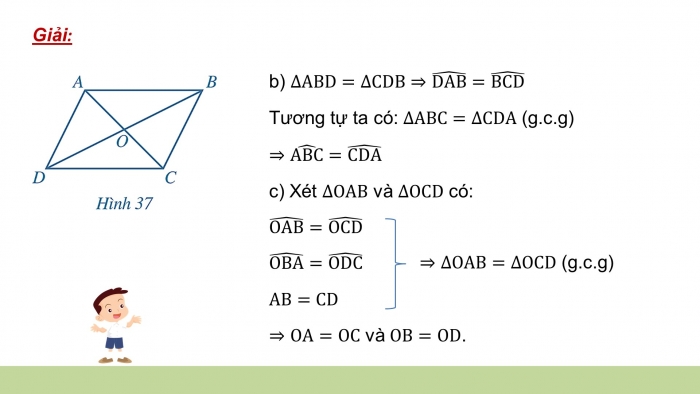
1. b)

Tương tự ta có:  (g.c.g)

1. c) Xét và có:

 và .

ĐỊNH LÍ

Trong một hình bình hành:

1. a) Các cạnh đối bằng nhau.
2. b) Các góc đối bằng nhau.
3. c) Hai đường chéo cắt nhau tại trung điểm của mỗi đường.

Ví dụ 2

Cho hai hình bình hành ABCD và BECD, AC cắt BD tại O (Hình 38). Chứng minh:     a) AB = BE;                           b) OB =  CE

Giải

Do ABCD là hình bình hành nên AB = CD, OB = OD =  BD

Do BECD là hình bình hành nên BE = CD, BD = CE

1. a) Từ AB = CD và BE = CD, ta suy ra AB = BE (vì cùng bằng CD).
2. b) Từ OB = BD và BD = CE, suy ra OB =

Luyện tập 1

Cho hình bình hành ABCD có , AB = 4 cm, BC = 5 cm. Tính số đo mỗi góc và độ dài các cạnh còn lại của hình bình hành ABCD.

Giải:

Do  là hình bình hành nên:

 ;

;

Có:  

Do đó .

3. DẤU HIỆU NHẬN BIẾT

HĐ 3: a) Cho tứ giác ABCD có AB = CD, BC = DA (Hình 39).

• Hai tam giác ABC và CDA có bằng nhau hay không? Từ đó, hãy so sánh các cặp góc:  và ;           và  .
• ABCD có phải là hình bình hành hay không?

1. b) Cho tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại trung điểm O của mỗi đường (Hình 40).

• Hai tam giác ABO và CDO có bằng nhau hay không? Từ đó, hãy so sánh các cặp góc:  và . Tương tự, so sánh  và .
• ABCD có phải là hình bình hành hay không?

Giải:

1. a) Xét và có:

 (gt);  (gt);  chung

 (c.c.c)

  và

Ta có:

 ở vị trí so le trong  

 ở vị trí so le trong  

Tứ giác  có  và  nên là hình bình hành.

Xét  và  có:

 (gt);  (đối đỉnh);  (gt)

  (c.g.c)

  hay

Tương tự ta có:  (c.g.c)

 hay

Ta có:  ở vị trí so le trong  

              ở vị trí so le trong  

Dấu hiệu nhận biết

• Tứ giác có hai cặp cạnh đối bằng nhau là hình bình hành.
• Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành.

Ví dụ 3