Giáo án điện tử Toán 8 cánh diều Chương 8 Bài 6: Trường hợp đồng dạng thứ nhất của tam giác
Bài giảng điện tử Toán 8 cánh diều. Giáo án powerpoint Chương 8 Bài 6: Trường hợp đồng dạng thứ nhất của tam giác. Giáo án thiết kế theo phong cách hiện đại, nội dung đầy đủ, đẹp mắt, tạo hứng thú học tập cho học sinh. Thầy, cô giáo có thể tham khảo.
Xem: => Giáo án toán 8 cánh diều
Các tài liệu bổ trợ khác
Xem toàn bộ: Giáo án điện tử toán 8 cánh diều
CHÀO MỪNG CÁC EM ĐẾN VỚI TIẾT HỌC!
KHỞI ĐỘNG
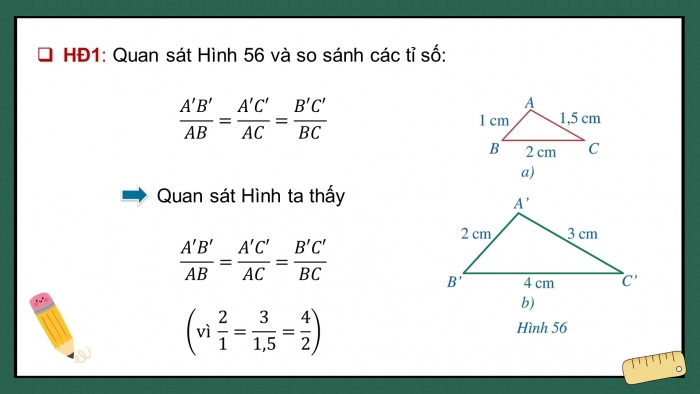
Mảnh đất trồng hoa của nhà bạn Hằng có dạng hình tam giác với độ dài các cạnh là . Bạn Hằng vẽ tam giác có độ dài các cạnh là để mô tả hình ảnh mảnh vườn đó (Hình 56a). Bạn Khôi nói rằng tam giác nhỏ quá và vẽ tam giác có độ dài các cạnh là (Hình 56b).
Hai tam giác và có đồng dạng với nhau hay không?
CHƯƠNG VIII. TAM GIÁC ĐỒNG DẠNG.
HÌNH ĐỒNG DẠNG
BÀI 6. TRƯỜNG HỢP ĐỒNG DẠNG THỨ NHẤT CỦA TAM GIÁC
NỘI DUNG BÀI HỌC
- Trường hợp đồng dạng thứ nhất: Cạnh – cạnh – cạnh
- HĐ1: Quan sát Hình 56 và so sánh các tỉ số:
Quan sát Hình ta thấy
Định lí
Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng với nhau.
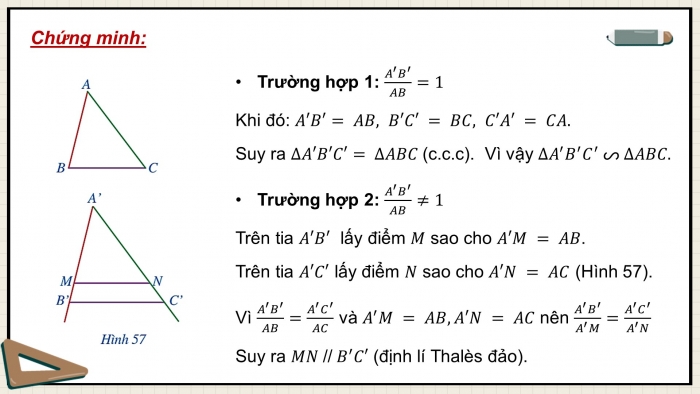
Chứng minh:
- Trường hợp 1:
Khi đó:
Suy ra (c.c.c). Vì vậy
- Trường hợp 2:
Trên tia lấy điểm sao cho .
Trên tia lấy điểm sao cho (Hình 57).
Vì và nên
Suy ra (định lí Thalès đảo).
Do đó (hệ quả của định lí Thalès).
Từ đó ta có suy ra
Xét hai tam giác và có:
Suy ra (c.c.c)
Do đó
Vì nên theo định lí trang 72 ta có
Vậy
Ví dụ 1: Quan sát Hình 58 và chỉ ra hai cặp tam giác đồng dạng:
Giải
Luyện tập 1
Cho tam giác có trọng tâm . Gọi lần lượt là trung điểm của . Chứng minh .
Giải
Ví dụ 2: Cho tam giác có lần lượt là trung điểm của các đoạn thẳng và lần lượt là trung điểm của các đoạn thẳng . Chứng minh .
Giải
Vì lần lượt là trung điểm của các cạnh nên là đường trung bình của tam giác .
Suy ra
Vì lần lượt là trung điểm của các cạnh nên là đường trung bình của tam giác
Suy ra
Từ hai đẳng thức (1) và (2), ta có
Chứng minh tương tự, ta cũng có
Vì nên
- Áp dụng trường hợp đồng dạng thứ nhất của tam giác vào tam giác vuông
- HĐ2: Cho hai tam giác và lần lượt vuông tại và (Hình 60) sao cho
- a) Tính và .
- b) So sánh các tỉ số
- c) Hai tam giác và có đồng dạng với nhau hay không?
Giải
- a) Xét vuông tại , theo định lí Pythagore ta có:
Suy ra . Do đó .
Xét ∆A’B’C’ vuông tại A’, theo định lí Pythagore ta có:
Suy ra Do đó .
- b) Ta có:
Do đó
- c) Xét và có:
Suy ra (c.c.c).
Định lí
Nếu cạnh huyền và một cạnh góc vuông của tam giác này tỉ lệ với cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.
GT |
|
KL |
|
Chứng minh:
- Trường hợp 1:
Khi đó:
Suy ra Vì vậy
- Trường hợp 2:
Trên tia lấy điểm thoả mãn .
Qua kẻ đường thẳng song song với cắt đường thẳng tại (Hình 61).
Ta có tức là
Xét hai tam giác vuông và , ta có
nên
Suy ra
Vì nên theo định lí trang 72 ta có
Vậy
Ví dụ 3: Quan sát Hình 62 và chỉ ra hai cặp tam giác đồng dạng:
Giải
Xét hai tam giác và , ta có và
Suy ra
Xét hai tam giác và , ta có và
Suy ra
Ví dụ 4: Cho tứ giác có
(Hình 63). Chứng minh tia là tia phân giác của góc .
Trên chỉ là 1 phần của giáo án. Giáo án khi tải về có đầy đủ nội dung của bài. Đủ nội dung của học kì I + học kì II
Hệ thống có đủ tài liệu:
- Giáo án điện tử toán 8 cánh diều (350k)
- Giáo án powerpoint toán 8 cánh diều (350k)
- Giáo án toán 8 cánh diều (300k)
- Giáo án dạy thêm toán 8 cánh diều (300k)
- Câu hỏi và bài tập trắc nghiệm toán 8 cánh diều (200k)
- Đề thi toán 8 cánh diều (200k)
- File word đáp án toán 8 cánh diều (100k)
- Bài tập file word toán 8 cánh diều (150k)
- Kiến thức trọng tâm Toán 8 cánh diều (150k)
- Đề kiểm tra 15 phút Toán 8 cánh diều (100k)
- Phiếu học tập theo bài Toán 8 cánh diều cả năm (150k)
- Trắc nghiệm dạng câu trả lời ngắn Toán 8 cánh diều cả năm (200k)
- Trắc nghiệm đúng sai Toán 8 cánh diều cả năm (200k)
=> Có thể chọn nâng cấp VIP với phí là 1050k để tải tất cả tài liệu ở trên
- Chỉ gửi 500k. Tải về dùng thực tế, 1 ngày sau mới gửi số còn lại.
Cách tải hoặc nâng cấp:
- Bước 1: Chuyển phí vào STK: 1214136868686 - cty Fidutech - MB(QR)
- Bước 2: Nhắn tin tới Zalo Fidutech - nhấn vào đây để thông báo và nhận tài liệu
Xem toàn bộ: Giáo án điện tử toán 8 cánh diều
ĐẦY ĐỦ GIÁO ÁN CÁC BỘ SÁCH KHÁC
GIÁO ÁN WORD LỚP 8 CÁNH DIỀU
GIÁO ÁN POWERPOINT LỚP 8 CÁNH DIỀU
GIÁO ÁN DẠY THÊM LỚP 8 CÁNH DIỀU
CÁCH ĐẶT MUA:
Liên hệ Zalo: Fidutech - nhấn vào đây