Giáo án điện tử Toán 9 cánh diều Bài 1: Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác

CHÀO MỪNG CÁC EM ĐẾN VỚI TIẾT HỌC MÔN TOÁN!

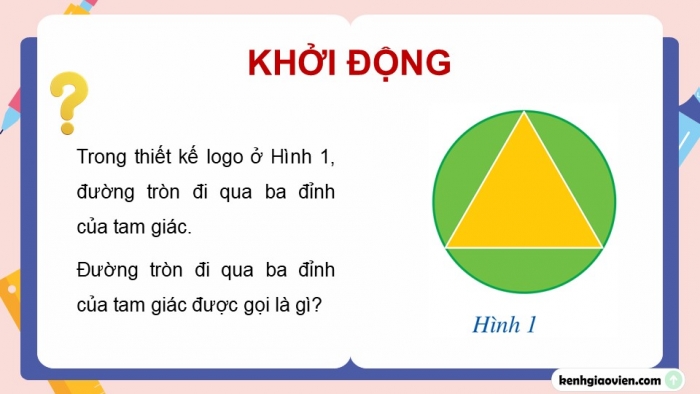
KHỞI ĐỘNG

Trong thiết kế logo ở Hình 1, đường tròn đi qua ba đỉnh của tam giác.

Đường tròn đi qua ba đỉnh của tam giác được gọi là gì?

BÀI 1. ĐƯỜNG TRÒN NGOẠI TIẾP. ĐƯỜNG TRÒN NỘI TIẾP TAM GIÁC

CHƯƠNG VIII. ĐƯỜNG TRÒN NGOẠI TIẾP VÀ ĐƯỜNG TRÒN NỘI TIẾP

01

NỘI DUNG BÀI HỌC

Đường tròn ngoại tiếp tam giác

02

Đường tròn nội tiếp tam giác

ĐƯỜNG TRÒN NGOẠI TIẾP TAM GIÁC

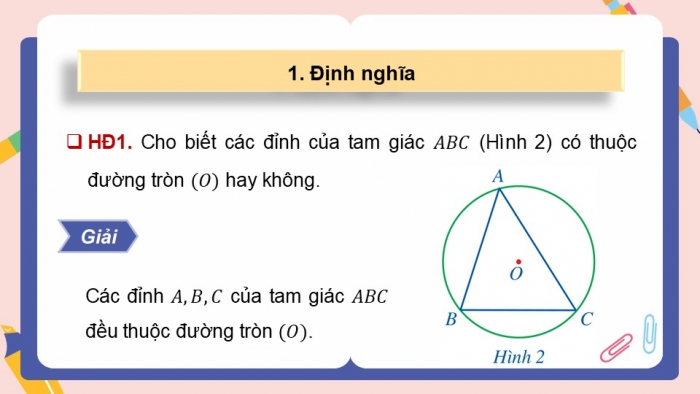
1. Định nghĩa

• HĐ1. Cho biết các đỉnh của tam giác (Hình 2) có thuộc đường tròn hay không.

Giải

Các đỉnh của tam giác đều thuộc đường tròn .

Ghi nhớ

Đường tròn đi qua ba đỉnh của tam giác được gọi là đường tròn ngoại tiếp tam giác đó.

Chú ý: Khi đường tròn ngoại tiếp tam giác , ta còn nói tam giác nội tiếp đường tròn .

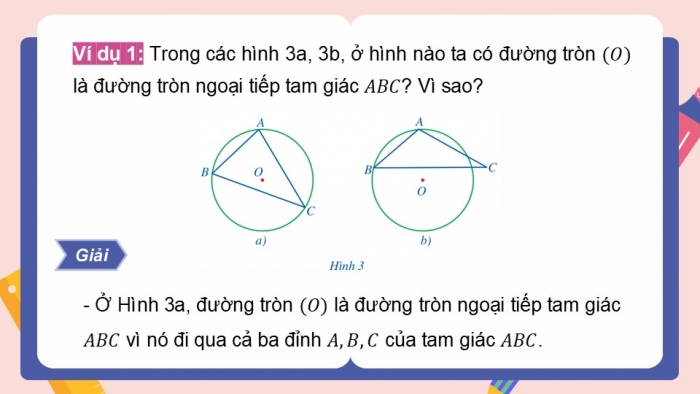
Ví dụ 1: Trong các hình 3a, 3b, ở hình nào ta có đường tròn là đường tròn ngoại tiếp tam giác ? Vì sao?

- Ở Hình 3a, đường tròn là đường tròn ngoại tiếp tam giác vì nó đi qua cả ba đỉnh của tam giác .

Giải

Ví dụ 1: Trong các hình 3a, 3b, ở hình nào ta có đường tròn là đường tròn ngoại tiếp tam giác ? Vì sao?

- Ở Hình 3b, đường tròn không là đường tròn ngoại tiếp tam giác vì nó không đi qua đỉnh của tam giác .

Giải

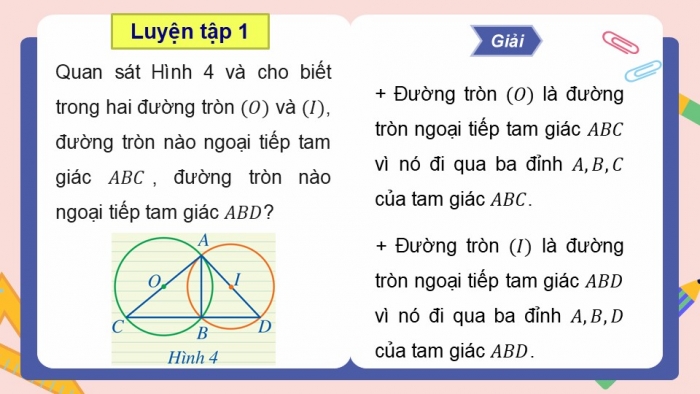
Luyện tập 1

Quan sát Hình 4 và cho biết trong hai đường tròn và , đường tròn nào ngoại tiếp tam giác , đường tròn nào ngoại tiếp tam giác ?

+ Đường tròn là đường tròn ngoại tiếp tam giác vì nó đi qua ba đỉnh của tam giác .

+ Đường tròn là đường tròn ngoại tiếp tam giác vì nó đi qua ba đỉnh của tam giác .

Giải

kenhgiaovien

/

• Bài giảng và giáo án này chỉ có duy nhất trên kenhgiaovien.com
• Bất cứ nơi nào đăng bán lại đều là đánh cắp bản quyền và hưởng lợi bất chính trên công sức của giáo viên.
• Vui lòng không tiếp tay cho hành vi xấu.

Zalo: 0386 168 725

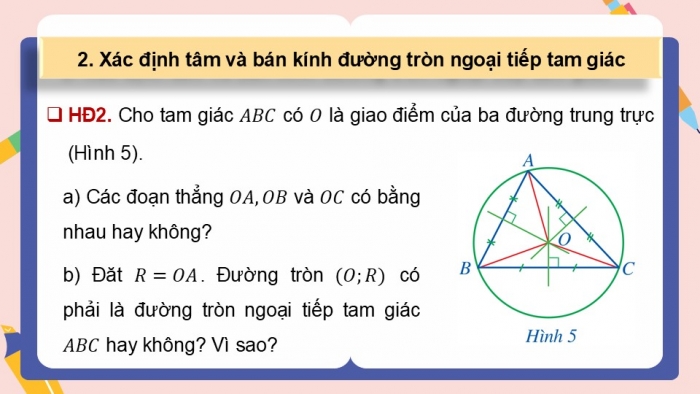
2. Xác định tâm và bán kính đường tròn ngoại tiếp tam giác

• HĐ2. Cho tam giác có là giao điểm của ba đường trung trực (Hình 5).

a) Các đoạn thẳng và có bằng nhau hay không?

b) Đăt . Đường tròn có phải là đường tròn ngoại tiếp tam giác hay không? Vì sao?

Giải

a) Vì là giao điểm của ba đường trung trực của tam giác nên điểm cách đều ba đỉnh của tam giác .

Do đó

b) Ta có nên ba điểm cùng nằm trên đường tròn hay đường tròn đi qua ba đỉnh của tam giác.

Vậy đường tròn là đường tròn ngoại tiếp tam giác .

Ghi nhớ

Tâm đường tròn ngoại tiếp tam giác là giao điểm ba đường trung trực của tam giác đó.

Bán kính đường tròn ngoại tiếp tam giác bằng khoảng cách từ giao điểm ba đường trung trực đến mỗi đỉnh của tam giác đó.

Nhận xét

• Vì ba đường trung trực của tam giác cùng đi qua một điểm nên tâm đường tròn ngoại tiếp tam giác là giao điểm hai đường trung trực bất kì của tam giác đó.
• Mỗi tam giác có đúng một đường tròn ngoại tiếp.

Ví dụ 2: Cho tam giác có góc tù. Dùng thước thẳng và compa vẽ đường tròn ngoại tiếp tam giác . (Hình 6)

Giải

- Dùng thước thẳng và compa vẽ hai đường trung trực của các cạnh và . Gọi điểm là giao điểm của hai đường trung trực đó.

- Dùng compa vẽ đường tròn . Đường tròn là đường tròn ngoại tiếp tam giác .

• HĐ3. Cho tam giác vuông tại . Gọi là trung điểm của (Hình 7). Đường tròn có phải là đường tròn ngoại tiếp của tam giác hay không?

Giải

Xét tam giác vuông tại có là đường trung tuyến ứng với cạnh huyền nên .

Mà là trung điểm của nên .

Do đó

• HĐ3. Cho tam giác vuông tại . Gọi là trung điểm của (Hình 7). Đường tròn có phải là đường tròn ngoại tiếp của tam giác hay không?

Giải

Vậy đường tròn đi qua các điểm của tam giác nên là đường tròn ngoại tiếp của tam giác .

Kết luận

Đường tròn ngoại tiếp tam giác vuông có tâm là trung điểm của cạnh huyền và bán kính bằng nửa cạnh huyền của tam giác vuông đó.

Ví dụ 3: Cho tam giác vuông tại có , . Tính bán kính của đường tròn ngoại tiếp tam giác theo .

Giải

Xét tam giác vuông tại , ta có (định lí Pythagore).

Suy ra .

Do đó .

Ví dụ 3: Cho tam giác vuông tại có , . Tính bán kính của đường tròn ngoại tiếp tam giác theo .

Giải

Vì tam giác vuông tại nên bán kính của đường tròn ngoại tiếp tam giác bằng nửa cạnh huyền . Vậy .

Luyện tập 2

Nêu cách sử dụng ê ke để xác định tâm của một đường tròn bất kì ki chưa biết tâm của nó.

Giải

Cách sử dụng ê ke để xác định tâm của một đường tròn bất kì khi chưa biết tâm của nó:

Bước 1. Lấy một điểm M bất kì trên đường tròn.

Bước 2. Đặt đỉnh vuông của ê ke trùng với điểm .

Luyện tập 2

Nêu cách sử dụng ê ke để xác định tâm của một đường tròn bất kì ki chưa biết tâm của nó.

Giải

Bước 3. Kẻ hai đường thẳng đi qua hai cạnh góc vuông của ê kê, hai đường thẳng này cắt đường tròn lần lượt tại hai điểm (khác điểm ).

Bước 4. Nối đoạn thẳng , khi đó là đường kính của đường tròn.

Luyện tập 2

Nêu cách sử dụng ê ke để xác định tâm của một đường tròn bất kì ki chưa biết tâm của nó.

Giải

Bước 5. Lấy là trung điểm của , khi đó là tâm của đường tròn đã cho.

Thật vậy, vuông tại nên đường tròn ngoại tiếp tam giác có tâm là trung điểm của cạnh huyền .

• HĐ4. Cho tam giác đều cạnh , ba đường trung tuyến cắt nhau tại trọng tâm (Hình 8).

a) có là các đường trung trực của tam giác hay không?

b) Điểm có là tâm đường tròn ngoại tiếp tam giác hay không?

c) Tính theo .

d) Tính theo .

b) Vì ba đường trung trực của tam giác cắt nhau tại điểm nên là tâm đường tròn ngoại tiếp tam giác

c) Vì đều nên

Xét vuông tại , ta có:

Giải

a) Vì đều nên ba đường trung tuyến , , cũng đồng thời là các đường trung trực của tam giác .

d) Tam giác có là đường trung tuyến và là trọng tâm của tam giác.

Do đó .

Vậy .

Giải

Kết luận

• Trong một tam giác đều, trọng tâm của tam giác đồng thời là tâm đường tròn ngoại tiếp của tam giác đó.
• Tam giác đều cạnh có bán kính đường tròn ngoại tiếp là .

Ví dụ 4: Ba vị trí ở một công viên là ba đỉnh của một tam giác đều cạnh 15 m. Người ta cần chọn vị trí cách đều ba vị trí để làm một cột đèn. Tính khoảng cách từ vị trí đến mỗi vị trí .

Giải

Vì cách đều ba đỉnh của tam giác đều nên là tâm đường tròn ngoại tiếp tam giác đều .

Suy ra khoảng cách từ vị trí đến mỗi vị trí là:

Luyện tập 3

Cho tam giác đều nội tiếp đường tròn . Tính .

Giải

Giả sử tam giác đều có cạnh bằng . Khi đó .

Vì tam giác đều nội tiếp đường tròn nên là trọng tâm của tam giác và bán kính đường tròn ngoại tiếp là .

Luyện tập 3

Cho tam giác đều nội tiếp đường tròn . Tính .

Giải

Suy ra

Vậy .

ĐƯỜNG TRÒN NỘI TIẾP TAM GIÁC

1. Định nghĩa

• HĐ5. Cho tam giác và đường tròn (Hình 9). Nêu vị trí tương đối của các đường thẳng với đường tròn .

Ta có: tại thuộc đường tròn nên là tiếp tuyến của đường tròn hay tiếp xúc với đường tròn tại .

Giải

1. Định nghĩa

• HĐ5. Cho tam giác và đường tròn (Hình 9). Nêu vị trí tương đối của các đường thẳng với đường tròn .

Tương tự, ta cũng có tiếp xúc với đường tròn lần lượt tại .

Vậy các đường thẳng tiếp xúc với đường tròn lần lượt tại .

Giải

Ghi nhớ

Đường tròn tiếp xúc với ba cạnh của tam giác được gọi là đường tròn nội tiếp tam giác đó.

Chú ý: Khi đường tròn nội tiếp tam giác , ta còn nói tam giác ngoại tiếp đường tròn .

Ví dụ 5: Tronng các hình 10a, 10b, ở hình nào ta có đường tròn là đường tròn nội tiếp tam giác ? Vì sao?

Giải

- Ở Hình 10a, đường tròn là đường tròn nội tiếp tam giác vì nó tiếp xúc với ba cạnh lần lượt tại .

Ví dụ 5: Tronng các hình 10a, 10b, ở hình nào ta có đường tròn là đường tròn nội tiếp tam giác ? Vì sao?

Giải

- Ở Hình 10b, đường tròn không là đường tròn nội tiếp tam giác vì nó không tiếp xúc với cạnh .

Luyện tập 4

Trong Hình 11, đường tròn là đường tròn nội tiếp những tam giác nào?

Giải

Đường tròn là đường tròn nội tiếp vì nó tiếp xúc với ba cạnh của tam giác.

Đường tròn cũng là đường tròn nội tiếp vì nó tiếp xúc với ba cạnh của tam giác.

2. Xác định tâm và bán kính đường tròn nội tiếp tam giác

• HĐ6. Cho tam giác có là giao điểm của ba đường phân giác. Gọi lần lượt là hình chiếu của trên các cạnh (Hình 12).

a) So sánh các đoạn thẳng và .

b) Đặt . Đường tròn có phải là đường tròn nội tiếp tam giác hay không? Vì sao?

Giải

b) Ta có nên ba điểm cùng nằm trên đường tròn .

Lại có nên đường tròn tiếp xúc với ba cạnh .

Vậy đường tròn là đường tròn nội tiếp tam giác

a) Vì là giao điểm của ba đường phân giác của tam giác nên điểm cách đều ba cạnh của tam giác .

Do đó .

Kết luận

Tâm đường tròn nội tiếp tam giác là giao điểm ba đường phân giác của tam giác đó.

Bán kính đường tròn nội tiếp tam giác bằng khoảng cách từ giao điểm ba đường phân giác đến mỗi cạnh của tam giác đó.

Nhận xét

• Vì ba đường phân giác của một tam giác cùng đi qua một điểm nên tâm đường tròn nội tiếp là giao điểm hai đường phân giác bất kì của tam giác đó.
• Mỗi tam giác có đúng một đường tròn nội tiếp.

Ví dụ 6: Cho tam giác . Dùng thước thẳng, ê ke và compa vẽ đường tròn nội tiếp tam giác .

Giải

- Dùng thước thẳng và compa vẽ hai đường phân giác của các góc và . Gọi điểm là giao điểm của hai đường phân giác đó.

Giải

- Dùng ê ke vẽ đường vuông góc kẻ từ đến đường thẳng .

- Dùng compa vẽ đường tròn . Đường tròn là đường tròn nội tiếp tam giác .

• HĐ7. Cho tam giác đều cạnh , ba đường trung tuyến cắt nhau tại trọng tâm (Hình 14).

a) có là các đường phân giác của tam giác hay không?

b) Điểm có làm tâm đường tròn nội tiếp tam giác hay không?

c) Tính theo .

a) Vì đều nên ba đường trung tuyến cũng đồng thời là các đường phân giác của tam giác .

b) Vì ba đường phân giác của tam giác cắt nhau tại điểm nên là tâm đường tròn nội tiếp tam giác .

Giải

Giải

c) Vì đều nên

Xét vuông tại , ta có:

Tam giác có là đường trung tuyến

và là trọng tâm của tam giác.

Do đó

Vậy .

Kết luận

Trong một tam giác đều, trọng tâm của tam giác đồng thời là tâm đường tròn nội tiếp tam giác đó.

Tam giác đều cạnh có bán kính đường tròn nội tiếp là .

Ví dụ 7: Một mảnh vườn có dạng tam giác đều cạnh 12 m. Người ta muốn trồng hoa ở phần đất bên trong đường tròn nội tiếp tam giác . Tính diện tích phần đất trồng hoa đó (theo đơn vị mét vuông, lấy và làm tròn kết quả đến hàng phần mười).

Giải

Gọi là đường tròn nội tiếp tam giác đều .

Suy ra bán kính của phần đất trồng hoa đó là:

--------------------------------------

--------------------- Còn tiếp ----------------------